Добавил:

Hist Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

Теория функций комплексного переменного

Файл:

ТФКП_1_2 / tfkp

.pdf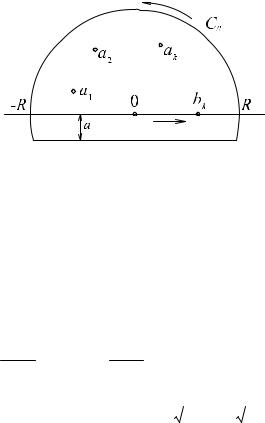

Скачиваний:

Добавлен:

11.05.2014

Размер:

1.91 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

Логинов А.С. Лекции по ТФКП

Обобщённая лемма (без доказательства). Если f(z) аналитична в {| z |> R0 , Im z > −a, a > 0}

кроме конечного числа особых точек ak {| Im z > 0} , и конечного числа полюсов первого порядка

bk	{Im z = 0} и lim max \| zf (z) \|= 0 , то
	R →∞ z CR
	∞
	∫ f (z)dz = 2πi∑Re s f (z) + πi∑Re s f ( z)
	−∞	ak	bk
	−∞

∞

x + 1

Пример 1.

I = ∫

x( x

+ 1)

−∞

1 + i

Re s = 1, Re s =

= −

(1 + i), I = πi +

2πi

−

= π .

i2i

2π

dϕ

Пример 2. I = ∫

, a > 1 .

+ cosϕ

2π

dϕ

2π

2eiϕ dϕ

I = ∫

= ∫

∫

, где С – единичная окружность.

iϕ

+ e

−iϕ

2ae

iϕ

+ e

i 2ϕ

0 a +

+ 1

+ 2az + 1

Корни знаменателя: z1 = −a + a2 − 1, z2 = −a − a2 − 1 . Внутри С расположен только один корень

2π

z . Поэтому

I =

2πi Re s

= 4π

z1 − z2

+ 2az + 1

2 a2 − 1

a2 − 1

∞ cos ax dx

Пример 3.

I = ∫

, a > 0, b > 0 .

+ b

∞

cos ax dx

∞

cos ax dx

∞

ia z

iaz

I = ∫

∫

Re ∫

2πi Re s

0 x + b

2 −∞ x + b

−∞ (z − ib)(z + ib) 2

(z − ib)(z + ib)

2πi

− ab

−ab

2bi

∞

3. Интегралы вида

∫eiλx

f (x)dx

−∞

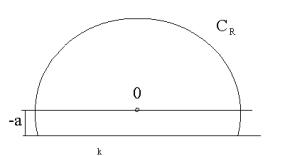
Лемма Жордана. Если f(z) аналитична в {| z |> R0 , Im z > −a, a > 0} и

M (R) = max | f (z) |→ 0, R → ∞ (CR - верхняя полуокружность).

C R

Логинов А.С. Лекции по ТФКП

∫eiλz

Тогда lim

f (z)dz = 0 для любого λ>0.

R →∞

C R

Доказательство. На окружности радиуса R имеем

eiλz

eiλR (cos t +i sin t )

= e−λR sin t

. Тогда,

учитывая неравенство sin t ≥

t,t [0, π ] , для окружности z(t)=Reit

получим

∫ f (z)eiλz dz

∫ f (Reit )eiλR (cos t + i sin t )i Reit

≤ M (R)R∫e−λR sin t dt =

C R

2λR

π / 2

= 2M (R)R ∫e−λR sin t dt ≤2M (R)R ∫ e−

t dt =

π π / 2

−λR

2λR

−λR

− λR

∫

t =2M (R)

− e

= M (R)

(1 − e ) → 0, R → ∞ .

= 2M (R)

2λ 0

2λ

Следствие. Если f(z) аналитична в {| z |> R0 , Im z > −a, a > 0} кроме конечного числа особых

точек ak {| Im z > 0} , и конечного числа полюсов первого порядка bk {Im z = 0} и

lim max | f (z) |= 0 , то

R →∞ z C R

∞

R →∞

∫

∑

∑ b

∫

eiλ x f (x)dx = lim

eiλz f

(z)dz =2πi

Re s eiλ z f

(z)

+ πi

Re s eiλ z f (z) .

−∞

C R [ − R, R ]

∞

x cos xdx

Пример. I

∫

x 2

− 2 x + 10

− ∞

∞

x cos xdx

∞

zeiz dz

∞

zeiz dz

∫

= Re ∫

= Re

∫

, a = 1 + 3i, b = 1 − 3i .

− 2x

+ 10

(z − a)(z − b)

−∞

− ∞

− 2z + 10

−∞

(1 + 3i)e

i −3

= π e−3

I = Re 2πi Re s

= Re 2πi

(cos1 − 3sin1)

a − b

− a)(z − b)

§3 Простейшие классы аналитических функций.

Определение 1. Однозначная функция f(z) называется целой, если она аналитична в С. Целая функция называется целой рациональной, если ∞ её полюс. Целая функция называется целой трансцендентной, если ∞ существенно особая точка.

Примеры. ez, cos z, sin z, Pn(z).

Свойства целых функций

1) Если ∞ устранимая изолированная особая точка целой функции f, то f есть константа.

Доказательство. Существует предел в бесконечности, поэтому f(z) ограничена в окрестности бесконечности, поэтому она постоянна по теореме Лиувилля.

2) Если ∞ полюс кратности n (n - натуральное), то f есть полином степени n. Доказательство.

Логинов А.С. Лекции по ТФКП

∞
f (z) = ∑c−kk + c0 + c1z + ... + cn zn , cn ≠ 0 , обозначим Pn (z) = c0 + c1z + ... + cn zn ,
k =1	z

Функция ϕ (z) = f (z) − Pn (z) будет, как разность двух целых функций, аналитической во

всей комплексной плоскости и имеет в ∞ устранимую особенность, следовательно, она константа по теореме Лиувилля.

Определение 2. Однозначная функция f мероморфна в С, если в любом круге нет других особых точек, кроме полюсов.

Теорема. Если ∞ - полюс для мероморфной функции f ( z) , то она рациональна.

Доказательство. Так как ∞ изолированная особая точка, то в расширенной комплексной плоскости имеется лишь конечное число полюсов a0 = ∞, a1 ,..., an . Выпишем разложения в ряд

Лорана в окрестности каждой из конечных точек ak :

−α m	∞
f (z) = ∑ckm (z − am )k + ∑ckm (z − am )k = ϕm (z) +ψ m (z), m = 1,..., n .
k = −1	k =0
Разложение в окрестности ∞ имеет вид:
α 0	−∞
f (z) = ∑ck0 zk + ∑ck0 zk = ϕ0 (z) +ψ 0 (z)
k =0	k = −1

Функции ϕm, m=0,…,n – рациональные.

F (z) = f (z) − ∑ϕm (z) имеет точки a0,…,an своими устранимыми особыми точками, поэтому

m =0

эта функция, после доопределения по непрерывности, будет ограниченной в С и следовательно константой.

Следствие. Рациональная функция представима в виде суммы многочлена и простейших

дробей вида (z − a)k . Это фактически доказано в предыдущей теореме.

Глава 7. Преобразование Лапласа.

Введение. Интегралы, зависящие от параметра.

Пусть С – кусочно гладкая, не ограниченная в одну сторону, кривая

Пусть f(z,ζ) определена при z D ( некоторая область ) и ζ С. Интеграл от параметра

определяется по формуле
F (z) = ∫ f (z,ζ )dζ = lim	∫ f (z,ζ )dζ
s →∞
C	C s

Этот интеграл называется сходящимся равномерно в D, если

ε > 0 s0 z D s > s0 : ∫ f (z,ζ )dζ − ∫ f (z,ζ )dζ < ε
C	C s

Признак Вейерштрасса. Если

1)для ζ С,z D : |f(z,ζ)|≤ g(ζ) , g(ζ) действительно-значная функция,

2)	∫g(ζ ) \| dζ \|	сходится, то ∫ f ( z,ζ )dζ сходится равномерно на D.
	С	C

§1 Преобразование Лапласа.

Логинов А.С. Лекции по ТФКП

Определение. Комплекснозначная функция f(t), t (-∞,∞) называется оригиналом, если

1)f(t)=0 при t < 0.

2)в (a,b) есть лишь конечное число разрывов первого рода. Иногда, дополнительно будет требоваться выполнение условия Липшица |f(t+h) - f(t)| ≤ A|h|α, для всех h,|h|≤ h0, α≤1 на интервалах непрерывности функции

3)	M s t :\| f (t) \|≤ Mest	(*)
Число s0 = inf s , S – множество тех s, для которых выполнено условие (*), называется
	s S
показателем роста оригинала.
Пример. Функция Хевисайда
		1, t ≥ 0
		H (t) =	,
		0, t < 0
показатель роста равен нулю.
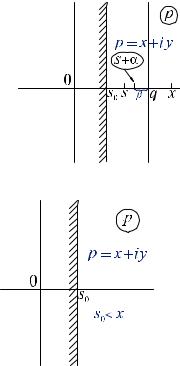
Изображением функции оригинала f(t) ( по Лапласу ) называют функцию комплексного
переменного p=x+iy, определяемую равенством
		∞
		F ( p) = ∫ f (t)e− pt dt
		0
Пишут F[ f ], F f , f F .
Замечание. Отметим, что если		f (t) оригинал, то и t k f (t) – также оригинал. Кроме того,
интеграл будет сходиться равномерно по параметру в любом множестве Re p ≥ q > s0 .

Это следует из признака Вейерштрасса с учетом

неравенств:

| t k f (t)e− pt |≤ Meαt est e− xt ≤ Me(α + s − x)t = Me− β t , β > 0 ,

где α из неравенства | t k |≤ Ceαt выбрано достаточно малым так, что s + α < q .Для функции имеется оценка: | f (t) |≤ Best

Теорема 1. Для любого оригинала	f (t) с
показателем s0 , изображение F ( p) определено в
полуплоскости x = Re p > s0 , является в этой
области аналитической функцией, стремящейся к 0
при x → ∞ ( равномерно относительно arg p ). При
этом
∞
F ' ( p) = ∫(−t) f (t)e− pt dt
0
Доказательство.
∞	∞

Сходимость интегралов F ( p) = ∫ f (t)e− pt dt и F ( p) = ∫tf (t)e− pt dt следует из сделанного

0	0
∞	∞

замечания. Обозначим U = Re F = ∫ f (t)e− xt cos yt dt , V = Im F = −∫ f (t)e− xt sin yt dt , p = x + iy .

0 0

Интегралы, полученные формальным дифференцированием

Логинов А.С. Лекции по ТФКП

	∞	∞
U x	= −∫tf (t)e−xt cos yt dt ,	U y = −∫tf (t)e−xt sin yt dt
	0	0
	∞	∞
Vx	= ∫tf (t)e− xt sin yt dt , Vy	= −∫tf (t)e− xt cos yt dt
	0	0

сходятся равномерно на любых отрезках изменения параметров (по параметру x, отрезок, где имеет место равномерная сходимость, должен лежать в области x > s0), поэтому исходные интегралы можно дифференцировать по параметру и выполнены условия Коши Римана. Далее, при

x = Re p > s > s будет выполнено:

| f (t) |≤ Mest и

∞

∫ f (t)e− pt dt

≤ ∫Mest e− xt dt = ∫Me( s − x )t dt =

∫de( s − x )t =

e( s − x )t

s − x

x − s

d k

F ( p)

∞

− pt

d k F

Следствие.

= ∫

(−t)

f (t)e

dt,

÷ (−t)

f (t)

Теорема 2. Если F÷f (f – кусочно гладкая ), то в точках непрерывности

f (t) имеет место

равенство

a + i∞

f (t) =

∫e pt F ( p)dp ,

2πi

a −i∞

где интеграл берётся вдоль любой

прямой Re p =a > s0, в смысле главного

значения

a + i∞

a + iR

∫e pt F ( p)dp = lim

∫e pt F ( p)dp

a −i∞

R →∞

a −iR

(без доказательства).

Теорема 3 ( Достаточные условия существования оригинала ). Если F(p) аналитична в

{Re p > s } и

a + i∞

F ( p)

≤

,α > 0 при p→∞, тогда интеграл

f (t) =

∫

e pt F ( p)dp, a > s не

p |1+α

2πi

a −i∞

зависит от a, является оригиналом и F ( p) = L[ f ] . ( только формулировка ).

§2 Свойства преобразования Лапласа

В этом параграфе везде под

f (t) понимается f (t)H (t)

(H - функция Хевисайда ).

Отметим, что 1 ÷

, Re p > 0; e p0 t ÷

, Re p > Re p

p − p0

1)Линейность.

αf(t)+βg(t)÷αF(p)+βG(p)

2) Свойство подобия. При α>0

f (αt) ÷

∞

− pt

∞

−

α t

∫ f (αt)e

∫

f (αt)e α

dαt =

3) Свойство запаздывания.

Логинов А.С. Лекции по ТФКП

Для τ > 0 выполнено: f (t − τ ) e− pτ F ( p) . Действительно

∞			∞			∞
∫ f (t − τ )e− pt dt = ∫ f (t − τ )e− p (t −τ )e− pτ d (t − τ ) =e− pτ ∫ f (t)e− pt dt = e− pτ F ( p)
0			0			−τ
4)	Как уже отмечалось, F ( n ) ( p) ÷				(−1)n t n f (t) , если взять f (t) = e p0 t ÷			1	, то


								p − p0
t ne p0 t ÷		n!
t ne p0 t ÷		( p − p	)n +1
	0
5)	Дифференцирование оригинала				f '(t) ÷ pF ( p) − f (0) или : F[ f '] = pF[ f ] − f (0) .
			∞	∞		∞	∞
			∞	∞			∞
Действительно ∫ f '(t)e− pt dt = ∫e− pt df (t) = f (t)e− pt							+ p∫ f (t)e− pt dt
			0	0		0	0
Следствие. f ( n) (t) ÷ pn F ( p) − p( n −1) f (0) − p(n − 2) f '(0) − ... − f ( n −1) (0) .
Доказательство. F[ f '] = pF[ f ] − f (0) ,

F[ f ''] = pF[ f '] − f '(0) = p( pF ( p) − f (0)) − f '(0) = p2 F ( p) − pf (0) − f '(0) . Далее, по индукции,

		n −1
доказывается равенство: F[ f ( n ) ] = pn F[ p] − ∑ pk f n −1− k (0) .
		k =0
6)	Интегрирование изображения
Если	f (t) ÷ F ( p), Re p > s и функция			f (t)	является оригиналом, то
Если	f (t) ÷ F ( p), Re p > s и функция				является оригиналом, то
	0			t
				t
			f (t)		∞
			f (t)		÷ ∫F (q)dq
				t	÷ ∫F (q)dq
				t	p
					p

Доказательство.

f (t)		∞	f (t)	e− pt dt, Q'( p) = −F ( p)
	÷ Q( p) = ∫

t		0	t

7)		Интегрирование оригинала.

Если f (t) ÷ F ( p), Re p > s0 , то

g(t)

∞

Q( p) = ∫F (q)dq + C,Q(∞) = 0 C = 0

= ∫ f (τ )dτ ÷ F ( p)

Доказательство. f (t) ÷ g'(t) ÷ pG( p) − g (0) = pG( p) откуда F(p)=pG(p) 8) Свертка оригиналов и умножение изображений.

Определение.

∞

( f * g )(t) = ∫ f (τ )g(t − τ )dτ

−∞

Отметим, что f*g=g*f, Сделать замену u = t - τ , dτ = -dt. f * g ÷ F ( p)G( p)

∞ ∞			∞	∞	∞	∞
∫ ∫ f (τ )g(t − τ )dτe− pt dt = ∫				f (τ )∫g(t − τ )e− pt dtdτ = ∫		f (τ )e− pτ ∫g(u)e− pu dudτ =F ( p)G( p)
0 −∞			−∞	0	−∞	0
Отметим, что если f, g – оригиналы, то и f*g – оригинал.
9)	Умножение оригиналов, свёртка изображений
		1	a + i∞
f (t)g(t) ÷		1	∫F (τ )G( p − τ )dτ
f (t)g(t) ÷		2πi	∫F (τ )G( p − τ )dτ
		2πi	a −i∞
			a −i∞

без доказательства.

10) Свойство смещения

F ( p − λ) ÷ eλt f (t)

Логинов А.С. Лекции по ТФКП

Доказательство из определения.

11)Первая теорема разложения (Теорема 1 Хевисайда).

∞

Если F(p) аналитична в {R<|p|<∞} и F ( p) = ∑

c− k

, то оригиналом является функция

k =1

∞

c−k

f (t) = H (t)∑

t k −1 .

k =1

(k −1)!

Доказательство. ∞ - устранимая особая точка, поэтому |F(p)|<M,|p|≥R.Положим

∞

p =

, Φ(q) = F

, Φ(q)

∑

qk , аналитична в круге |q|<1/R, поэтому неравенство Коши даёт

− k

k =1

∞

c− k

∞

k −1

для коэффициентов |c-k|<MRk и

∑

t k −1

≤ A∑

(R | t |)

= AeR|t| .

(k − 1)!

k =1

k =1 (k − 1)!

Таким образом, исходный ряд мажорируется сходящимся степенным рядом в любом круге. В

∞

c− k

этом случае ряд

∑

t k −1

можно почленно интегрировать

k =1

(k − 1)!

∞

c− k

∞

c− k

e− pt

∑

t k −1dt =

∑

e− ptt k −1dt по свойству 4) при r→∞

∫

(k − 1)! ∫

k =1

(k − 1)!

k =1

∞

− pt

k −1

(k − 1)!

∫e

dt =

= 1,2,... , поэтому

, k

∞

c− k

∞

c− k

∫e− pt

∑

t k −1dt =

∑

= F ( p)

k =1

(k − 1)!

k =1

12)Вторая теорема Хевисайда. Если

1.F(p) мероморфна в некоторой полуплоскости Re p > s0 и F(∞)=0

	a +i∞
2.	a > s0 ∫	F ( p)	dp	< ∞

a-i∞

3.F(p)→0 при p→∞ равномерно относительно arg p

Тогда оригиналом для F служит функция f (t) = H (t)∑Re sF ( p)e pt по полюсам функции F в

pk pk

порядке убывания их модулей.

Доказательство. При сделанных предположениях для оригинала f (t) F ( p) выполнено

	1	a + i∞
равенство: f (t) =		∫F ( p)e pt dp .
	2πi
		a −i∞

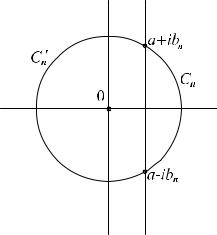
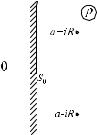
Обозначим через Cn ' часть окружности

Cn, расположенную слева от прямой Re p = a, через a±ibn обозначим точки пересечения Cn с этой прямой и через n контур, составленный из [a-ib,a+ib] и Cn ' , проходимый против часовой стрелки.

Логинов А.С. Лекции по ТФКП

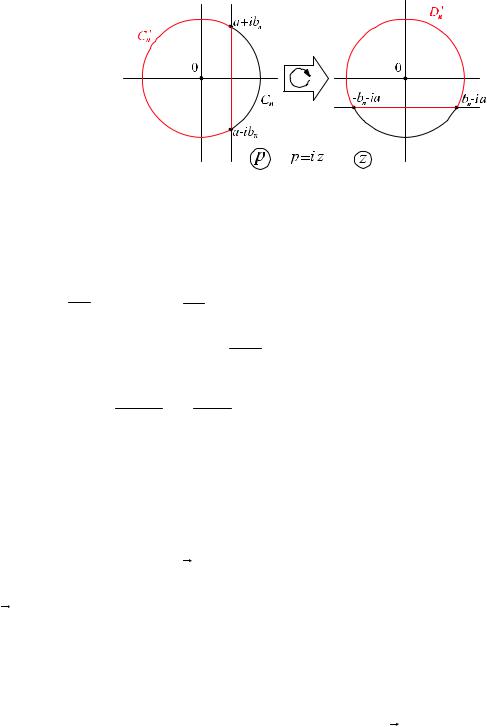
Положим:

p = iz, z = x + iy, p = u + iv = − y + ix , тогда, если

p Cn ' = {Re u < a} , то

z Dn ' = {Im z > −a}.

Делая в интеграле

∫e pt F ( p)dp замену

p = iz , получим:

∫e pt F ( p)dp =i ∫eizt F (iz)dz . По

C 'n

D ' n

лемме Жордана при t > 0 будет выполнено: lim

∫e pt F ( p)dp = 0 .

n →∞

C ' n

Поэтому при t > 0

f (t) = 1

a + i∞

e pt F ( p)dp = lim ∑ Re s e pt F ( p) , ч.т.д.

∫

F ( p)e pt dp =

lim

∫

2πi

n →∞

n →∞ p

a −i∞

Следствие. Если функция F ( p) = A( p)

дробно-рациональная и дробь правильная, то

B( p)

оригиналом ее служит функция

nk −1

{F ( p)( p − pk )nk e pt }

f (t) = H (t)∑

lim

−1

k =1 (nk

− 1)!

p → pk

где pk полюсы функции F(p) кратностей nk , сумма берется по всем полюсам.

Глава 8. Приложения.

						§1 Комплексный потенциал
		Рассмотрим плоское поле A = (P, Q,0) = P + iQ
		Соленоидальное поле ( без источников и стоков, поток через замкнутую кривую равен нулю )
div A =		∂P +			∂Q = 0 . Тогда для формы − Qdx + Pdx выполнены условия полного дифференциала
		∂x			∂y
∂			∂
	(P)	−		(−Q) = 0 , поэтому существует функция v : dv = −Qdx + Pdy , для неё
∂x	(P)	−	∂y
		∂v = −Q, ∂v = P				(1)
		∂x			∂y

Определение. Функцией тока плоского соленоидального поля A = (P,Q) = P + iQ называется дважды непрерывно дифференцируемая функция v, удовлетворяющая соотношениям (1).

Функция тока находится по формуле

v(x, y) = ∫− Qdx + Pdy + Const

					Логинов А.С. Лекции по ТФКП
1)	Потенциальное ( безвихревое поле ) rot A = (0,0,			∂Q −	∂P ) = 0 . В этом случае
				∂x	∂y
		∂u = P,	∂u = Q, u(x, y) =	z
существует потенциал u : grad u = A,		∂u = P,	∂u = Q, u(x, y) =	∫Pdx + Qdy + Const .
		∂x	∂y	z0
				z0

2)Поле и потенциальное и соленоидальное. В этом случае, как это следует из 1) и 2),

выполнены условия
∂u =	∂v ,	∂u = −	∂v	(2),
∂x	∂y	∂y	∂x

которые являются условиями Коши-Римана для функции f(z)=u(x,y)+iv(x,y).

Эта функция называется комплексным потенциалом данного поля. Отметим, что в плоском поле без источников и вихрей функция тока и потенциал являются гармоническими сопряженными функциями. Как это следует из 1)-2)

	∂u			∂v
A =			−		= f '(z)
	∂x	+ i
				∂x

Для такого поля поток

N = ∫(A, n)ds = ∫((P, Q), (dy,−dx)) = ∫− Qdx + Pdy = ∫dv = Im ∫df = Im ∫ f ' (z)dz

C C C C C C

3)Восстановления функции тока по потенциалу.

Если потенциал u является гармонической функцией, то форма –Qdx+Pdy является полным дифференциалом и функция тока v восстанавливается по формуле

v(x, y) = ∫− Qdx + Pdy + Const

Аналогичным образом может быть восстановлен потенциал u по функции тока v, если она гармонична.

§2 Операционное исчисление

Дана задача Коши

L[x] = ∑ak

k = 0

d k x	=a		x(n ) + a		x( n −1) + ...a	x = f (t)
				n −1
dt k		n			0	, an≠0.	(1)

x( k ) (0) = xk , k = 0,..., n − 1

Будем предполагать, что f(t) и x(t) вместе со всеми производными до n-го порядка являются оригиналами. Положим x(t) X(p), f(t) F(p). Из свойств преобразования Лапласа следует, что

		k −1	k −1
F[x( k ) ] = pk X ( p) − ∑ p j x( k −1− j ) (0) =pk X ( p) − ∑ p j xk −1− j
		j =0	j =0
Отсюда, применяя преобразование Лапласа к (1) получим
n		k −1
F[L[x]] = ∑ak pk X ( p) − ∑ p j xk −1− j = F ( p) , или
k =0		j = 0
n	n	k −1
X ( p)∑ak pk − ∑ak ∑ p j xk −1− j = F ( p), X ( p) A( p) − B( p) = F ( p) .
k =0	k =0	j =0

Таким образом,

X ( p) = F ( p) + B( p) , находя оригинал x(t) X(p) для функции X(p), получим решение задачи

A( p)

Коши.

Таблица основных свойств преобразования Лапласа

Логинов А.С. Лекции по ТФКП

∞

a + i∞

F ( p) = ∫ f (t)e− pt dt

f (t) =

∫e pt F ( p)dp

2πi

a −i∞

αf(t)+βg(t)÷αF(p)+βG(p)

1 ÷

, Re p > 0;

e p0 t ÷

, Re p > Re p

t ne p0 t ÷

− p

)n +1

( p

α>0 , f (αt) ÷

τ>0, f(t-τ)÷e-pτF(p)

λt

f(t)

F(p-λ)÷e

(−t)k f (t) ÷

dpk

f’(t)÷pF(p)-f(0),

f(n)(t)÷pnF(p)-pn-1f(0)-…-f(n-1)(0)

f (t)

∞

F ( p)

÷ ∫F (q)dq

∫ f (τ )dτ ÷

Таблица некоторых преобразований Лапласа

Оригинал

Изображение

tα (α>-1)

(α + 1)

pα +1

e-λt

p + λ

e-λt tα (α>-1)

(α + 1)

( p + λ)α +1

sin ωt

p2 + ω 2

cos ωt

p2 + ω 2

tn sin ωt

Im( p + iω )n +1

( p2 + ω 2 )n +1

tn cos ωt

Re( p + iω )n +1

( p2 + ω 2 )n +1

e-λt sin (ωt+α)

ω cosα + ( p + λ) sinα

( p + λ)2 + ω 2

e-λt cos (ωt+α)

− ω sinα + ( p + λ) cosα

( p + λ)2 + ω 2

sh ωt

p2 − ω 2

ch ωt

p2 − ω 2

ebt − eat

p − a

p − b

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

Соседние файлы в папке ТФКП_1_2

#
11.05.20141.91 Mб56tfkp.pdf
#
11.05.2014255.18 Кб57tfkp2.pdf