
ТФКП_1_2 / tfkp
.pdf
Логинов А.С. Лекции по ТФКП
Пример. Функция Жуковского 0.2 ≤| z |≤ 2,0 ≤ arg z ≤ π .
2
Функция Жуковского 1 ≤| z |≤ 2,0 ≤ arg z ≤ 2π .
Щель [−1,1] на действительной оси получена в результате сплющивания единичной окружности .
2.Обратная функция |
|
|
|
|
|
|
|
||||
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
D* = C \ [−1,1] в плоскости w, |
||||||
w = |
|
z + |
|
, z = w + |
w |
|
− 1 . Рассмотрим область |
||||
|
|
|
|||||||||
|
2 |
|
z |
|
|
|
|
|
|
|
|
плоскость с щелью [−1,1] . Первая однозначная ветвь f1(w) переводит D* в |z|<1, вторая ветвь f2(w)
переводит D* в |z|>1. Точки w=±1 являются точками ветвления.
31

|
|
|
|
|
|
Логинов А.С. Лекции по ТФКП |
|
z − |
|
|
§7 Таблица некоторых конформных отображений. |
||
1) w = eiϕ |
z |
0 |
, точка z |
|
отображается в 0, симметричная относительно единичной |
|
|
|
|
0 |
|||
1 − z0 z |
|
|||||
|
|
|||||
окружности точка 1 отображается в ∞ , поэтому, образом единичной окружности будет единичная z0
окружность.
|
|
|
|
|
→ 0, |
|
|
→ ∞, w = eiϕ |
z − |
z0 |
|
, |
|
u |
|
= 1 . |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2) Верхняя полуплоскость на единичный круг. z |
|
z |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
0 |
0 |
z − z0 |
u |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π
3) Угол { z: arg z (0, α),0 <α < 2π } на верхнюю полуплоскость w = zα . Напоминание
z β = r β eiβϕ .
4)В частности w=z2 отображает первый квадрант на верхнюю полуплоскость.
5)Плоскость с разрезом по положительной части вещественной оси на верхнюю
полуплоскость w = 
 z
z
6)
w |
a |
0 |
|
z |
w=e z |
ai |
|
0 |
7) Частный случай
32

Логинов А.С. Лекции по ТФКП
w
0 |
w=e |
z |
z |
|
||
|
|
|
|
|
0 |
8) Частный случай
w
w=e |
z |
z |
|
||
|
|
|
0 |
|
|
9)
|
w = |
1 |
( z + |
1 ) |
|
|
2 |
|
z |
w |
|
|
|
|
-1 |
1 |
|
|
|
|
0 |
|
|
|
10)
|
w = |
1 |
( z + |
1 ) |
|
|
2 |
|
z |
w |
|
|
|
|
-1 |
1 |
|
|
|
|
0 |
|
|
|
iz
0 1
1
z
i
01 
11)
|
|
w = |
1 |
|
|
|
2 |
w |
|
|
|
-1 |
0 |
1 |
|
|
|
33 |
|
( z + |
1 ) |
|
|
z |
|
|
|
z |
|
i |
|
|
0 |
1 |
Логинов А.С. Лекции по ТФКП
|
1 |
|
1 |
|
≤ arg z ≤ π |
|
w = |
|
z + |
|
0.1 |
≤| z |≤ 1, 0 |
|
|
|
|||||
|
2 |
|
z |
|
|
|
12)
w = |
1 |
( z + |
1 ) |
|
||
|
2 |
|
|
z |
|
|
w |
|
|
|
|
i |
z |
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
1 |
w = |
1 |
( z + |
1 ) |
|
||
|
|
2 |
|
|
z |
|
w |
|
|
-1 |
0 |
1 |
13) |
|
|
z |
0 |
14)
w |
i |
|
|
|
|
|
0 |
1 |
z |
Пример. Отобразить область
34

Логинов А.С. Лекции по ТФКП
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
w1 = e |
, w2 |
= |
|
+ |
|
= |
|
|
+ |
|
|
|
|
|
|
|
|
|||||||||
2 |
w1 |
w1 |
, w3 |
2 |
w2 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
w2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример.
w1 = z + 
 z2 − 1 (нужная ветвь) на верхнюю полуплоскость, затем w2=w12. Пример. Отобразить верхнюю полуплоскость с вырезанными полукругами
z2 − 1 (нужная ветвь) на верхнюю полуплоскость, затем w2=w12. Пример. Отобразить верхнюю полуплоскость с вырезанными полукругами
| z + 1 |< 1,| z − 1 |< 1 на верхнюю полуплоскость.
Все три обобщенные окружности γ1 ,γ 2 ,γ 3 проходят через точку 0, поэтому, если перевести 0
в ∞ отображением w = |
1 |
, то образы γ |
*,γ |
|
*,γ |
|
* будут прямыми линиями. Беря какие либо |
|
2 |
3 |
|||||
1 |
z |
1 |
|
|
|
||
|
|
|
|
|
|
|
симметричные точки относительно γ1 ,γ 2 ,γ 3 , найдем симметричные точки относительно прямых
γ1*,γ 2 *,γ 3 * в плоскости w1 . Возьмем в качестве симметричных точек относительно γ1 точки i,−i ,
образами которых будут − i,i и поэтому γ1 * будет вещественной осью. Для γ 2 возьмем 1, ∞ ,
образами которых будут 1,0, следовательно γ 2 * - вертикальная прямая, проходящая через точку 1/2.
Для γ 3 * возьмем -1, ∞ с образами -1,0. γ 3 * - вертикальная прямая, проходящая через точку -1/2.
35
Логинов А.С. Лекции по ТФКП
w1
-1/2
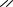
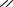
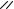
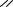
 1/2
1/2
0
|
Сделаем поворот на 90 |
|
|
градусов и сдвиг вверх на 1/2: |
i |
||
|
π |
|
|
w |
= ei 2 w + i . В результате |
w2 |
|
2 |
1 |
2 |
|
|
|
|
|
|
получаем полуполосу, |
|
|
|
показанную не рисунке. |
0 |
|
|
|
|
|
Далее растяжение в π раз: w3 = πw2 . Полученную полу-полосу переведем в верхнюю плоскость с вырезанным полукругом: w4 = ew3 , которая переводится в верхнюю полуплоскость
|
= |
|
= 1 |
|
+ 1 |
|
|
||
|
|
|
|
|
|||||
функцией Жуковского: w |
|
w5 |
|
2 |
w4 |
|
w4 |
|
. Итоговое отображение получается суперпозицией |
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
( πw2 |
|
|
) |
|
|
i |
|
i |
π |
|
|
|
|
|
−πw2 |
|
|
|
|
2 z |
||||||
найденных отображение: w( z) = w5 (w4 |
(w3 (w2 |
(w1 |
(z)))))= |
e |
+ e |
|
|
= ch |
π |
|
+ e |
|
|
. |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
Глава 4. Теория интеграла
Далее всюду в этой главе рассматриваются однозначные функции. §1. Понятие интеграла. Теорема Коши.
1.Интеграл и его свойства. Для кривой γ и функции f(z), определенной на ней,
n −1
рассматриваются интегральные суммы ∑ f (ζ k )(zk +1 − zk ) .
k =0
 k+1
k+1
Интеграл определяется, как предел этих сумм в стандартном смысле (характеристика стремится к нулю, предел не зависит от выбора разбиения и промежуточных точек ) и обозначается
∫ f (z)dz . Если кривая имеет параметризацию z(t), t [α,β], интегральные суммы в определении будут
γ
выглядеть следующим образом
n −1 |
n −1 |
∑ f (z(ξk ))(z(tk +1 ) − z(tk )) =∑ f ( z(ξk ))z'(θk ) tk . |
|
k =0 |
k =0 |
Для непрерывной функции f(z) и непрерывно дифференцируемой кривой z(t), t [α,β] эти
β
суммы будут сходиться к интегралу ∫ f (z(t))z'(t)dt . Расписывая действительную и мнимую части,
α
интеграл можно выразить через криволинейные интегралы
36

Логинов А.С. Лекции по ТФКП
∫ f (z)dz = ∫udx − vdy + i∫vdx + udy .
γ |
γ |
γ |
Это равенство можно принять за определение интеграла в случае, когда последние два интеграла существуют.
Свойства интеграла по заданной кривой:
1) Линейность: ∫(αf (z) + βg(z))dz = α ∫ f (z)dz + β ∫g (z)dz .
γ |
γ |
γ |
2)Аддитивность по множеству:
∫f (z)dz = ∫ f (z)dz + ∫ f (z)dz .
γ η γ η
|
3) |
∫ f (z)dz = − ∫ f (z)dz . |
||||
|
|
|
γ |
|
|
γ − |
|
4) |
|
∫ f (z)dz |
≤ max | f (z) | l , где l – длина кривой. Это неравенство следует из определения |
||
|
|
|
γ |
|
|
z γ |
|
|
|
|
|
|
|
(оценка интегральных сумм). |
||||||
|
5) |
Если γ - кусочно гладкая и fk(ζ) сходится равномерно на γ к f(ζ), то |
||||
lim |
fk (ζ )dζ = |
∫ |
f (ζ )dζ . Это следует из предыдущего свойства. |
|||
k →∞ ∫ |
|
|
|
|
|
|
γ |
|
|
|
γ |
|
|
|
6) |
Определение интеграла по границе многосвязной области ∂D= 0 1 … m . |
||||
|
|
|
m |
|
|
|
∫ f ( z)dz = ∑ ∫ f (z)dz . Обход по каждому связному куску границы происходит так, что область |
||||||
∂D |
|
|
k = 0 |
|
|
|
|
|
|
k |
|
|
|
остается слева
2.Теорема Коши.
Если D- ограниченная область, ΔD, граница которой ∂Δ - кусочно гладкая Жорданова кривая из D, гомотопная нулю (область, ограниченная этой кривой, односвязна ) и f аналитическая в
D, то ∫ f (z)dz = 0 .
∂
Доказательство. Для действительной и мнимой частей интеграла воспользуемся формулой Грина и условиями Коши-Римана:
∫ f (z)dz = ∫udx − vdy + i ∫vdx + udy = ∫∫(−vx − uy )dxdy + i∫∫(ux − vy )dxdy = 0
∂ ∂ ∂
Формула Грина справедлива и для многосвязных областей. Поэтому справедлива
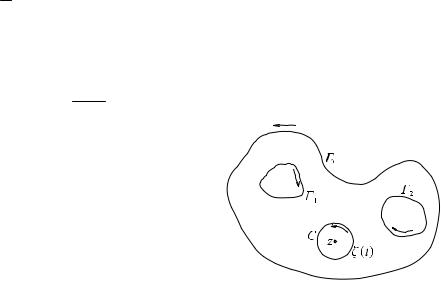
Обобщенная теорема Коши. Пусть D- ограниченная область с границей ∂D= 0 1 … m ,
а f функция, аналитическая в D и непрерывная в D = D U ∂D , тогда ∫ f (z)dz = 0 .
∂D
Следствие. В области D интеграл ∫ f (z)dz не зависит от пути интегрирования, а только
γ
от начальной и конечной точек кривой.
Таким образом, интеграл от аналитической функции в многосвязной области D не изменяется, если путь интегрирования непрерывно деформировать, оставляя неподвижными концы.
§2 Интеграл Коши
1.Интегральная формула Коши.
37
Логинов А.С. Лекции по ТФКП
Пусть D - m-связная область с границей ∂D= 0 1 … m-1 и f – аналитическая в D,
непрерывная в D = D ∂D функция. Имеет место формула
1 |
∫ |
f (ζ ) |
|
f (z), z D |
|||
|
|
dζ = 0, z |
|
= D ∂D |
|||
2πi |
ζ − z |
||||||
D |
|||||||
|
∂D |
|
|
|
|
|
|
Доказательство. Если z D∂D, то равенство нулю интеграла следует из аналитичности
f (ζ )
подинтегральной функции ζ − z для всех ζ D.
Пусть C – окружность с центром в z: ζ(t)=z+reit достаточно малого радиуса.
Для области с границей
∂D C − точка z является внешней.
|
|
|
В этом случае, согласно обобщенной теореме Коши |
|
∫ |
− |
ζ − z |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
f (ζ ) dζ = 0 , откуда следует, что |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂D C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
f (ζ )dζ |
|
|
|
|
f (ζ )dζ |
ζ |
it |
|
∫ |
|
f (ζ ) |
dζ |
|
|
2π |
f (z + reit ) |
|
|
|
it |
|||||||||||||||||||||
∫ |
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
ζ − z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
= |
|
|
|
|
|
|
. Так как d |
|
=r i e |
dt, то |
= |
|
|
|
|
|
|
|
it |
|
|
ire |
dt = |
||||||||||||||||||
|
|
|
ζ − z |
|
|
∂D ζ − z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
re |
|
|
|
|
|
|
|
||||||||||
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
i ∫ f (z + reit )dt = 2πif (z + reiθ ) . |
Последнее равенство следует из теоремы о среднем с некоторой |
|||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
промежуточной точкой θ . В полученном равенстве |
f ( z + reiθ ) = |
|
1 |
|
|
f (ζ )dζ |
переходим к |
|||||||||||||||||||||||||||||||||||||
|
2πi |
∫ |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ζ − z |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂D |
|
|
|
|
|
|
пределу при r → 0 и получаем требуемое равенство |
f (z) = |
1 |
|
|
∫ |
|
f (ζ )dζ |
Отметим, что |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
. |
|||||||||||||||||||||||||||||||||||||||
2πi |
|
|
ζ − z |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (ζ )dζ |
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
∫ |
|
|
= i ∫ f (z + reit )dt , то есть, последний интеграл |
|
∫ f ( z + reit )dt является константой, |
|||||||||||||||||||||||||||||||||||||||
|
ζ − z |
|
|
|||||||||||||||||||||||||||||||||||||||||
∂D |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
другими словами, не зависит от r. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
Следствие. Теорема о среднем. Если f непрерывна на |z| ≤ r и аналитическая в |z|<r, то |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( z ) = |
1 |
|
2π f (z + reit )dt |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
∫ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.Интеграл типа Коши. Интегралом типа Коши называется интеграл |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
F (z) = |
|
|
1 |
∫ |
ϕ (ζ ) dζ , где - кусочно-гладкая замкнутая кривая Жордана, ограничивающая |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
πi |
|
ζ − z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
односвязную область D, а ϕ - непрерывная на функция. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
Теорема. Интеграл типа Коши является аналитической функцией в области D и |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F ( n ) ( z ) = |
|
|
n! |
|
∫ |
|
ϕ (ζ ) |
|
|
dζ |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− z ) |
n +1 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2πi (ζ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Доказательство. Граница Г предполагается спрямляемой. Обозначим ее длину через l. Выпишем равенства, необходимые для вычисления производной:
38

Логинов А.С. Лекции по ТФКП
F (z) − F (z |
) |
|
1 |
|
ϕ (ζ ) |
|
|
|
1 |
|
|
1 |
|
1 |
|
1 |
|
|
1 |
|
|
|
0 |
|
− |
|
∫ |
|
|
dζ |
= |
|
∫ϕ (ζ ) |
|
|
|
− |
|
|
− |
|
|
dζ |
|
|
z − z0 |
|
2πi |
(ζ − z0 ) |
2 |
2πi |
|
ζ − z |
|
(ζ − z0 ) |
2 |
. |
|||||||||||
|
|
|
|
|
|
|
z − z0 |
|
ζ − z0 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выражение внутри второго интеграла преобразуется к виду:
1 |
|
1 |
− |
1 |
|
− |
1 |
2 |
= |
1 |
− |
1 |
2 |
= |
z − z |
0 |
. |
|
|
|
|
|
|
|
|
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z − z0 |
|
ζ − z |
|
ζ − z0 |
|
(ζ − z0 ) |
|
|
(ζ − z)(ζ − z0 ) |
|
(ζ − z0 ) |
|
|
(ζ − z0 ) (ζ − z) |
|
||
Выберем δ окрестность точки z0 , целиком лежащую в области D
|
Если |z - z0|< δ , то расстояние от до таких точек z будет больше чем δ/2, тогда, если ζ , |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z − z0 |
|
< |
| z − z0 | |
8 , откуда следует неравенство |
|
|
|
|
|
|
||||||||||||||||||
то |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
(ζ − z |
0 |
)2 (ζ − z) |
|
|
|
δ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
F ( z) − F ( z |
) |
− |
1 |
|
∫ |
|
ϕ(ζ ) |
|
dζ |
|
< |
l |
max | ϕ(ζ ) | |
| z − z |
| |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
8 . |
|||||||||||||
|
|
|
|
z − z0 |
|
2πi |
(ζ − z0 ) |
2 |
2π |
|
δ |
3 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Таким образом, существует lim |
F ( z) − F ( z0 ) |
= |
1 |
∫ |
ϕ(ζ ) |
|
|
dζ . Аналогичным образом |
|||||||||||||||||||||
|
|
2πi |
(ζ − z0 ) |
2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z→z0 |
|
z − z0 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
можно доказать существование старших производных и формулу для их вычисления.
§3 Первообразная.
1.Теорема Морера.
z
Теорема. Пусть D односвязная область, f(ζ) непрерывна в D и интеграл F ( z) = ∫ f (ζ )dζ ,
z0
z,z0 D не зависит от пути интегрирования, или, что тоже, ∫ f (ζ )dζ = 0 для любой замкнутой
γ
кривой Жордана, лежащей в D. Тогда F(z) аналитическая в D и ее производная F′(z)=f(z). Доказательство.
Рассмотрим две точки z и z+ z, путь из z0 в z обозначим γ, путь из z0 в z+ z пусть будет γ γ1,
где γ1 - отрезок: z(t)=z+ z t, t [0,1].
Тогда
|
F (z + z) − F (z) |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
− f |
(z) |
= |
|
|
|
∫ f (ζ )dζ − ∫ f (ζ )dζ |
− f (z) |
= |
|
∫ f (ζ )dζ − f (z) |
= |
|||
|
|
|
|
|
|
|||||||||||||
|
|
|
z |
|
|
|
z |
γ γ 1 |
γ |
|
|
z |
γ 1 |
|
||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
∫ f ( z + zt) |
zdt − f ( z) |
= |
∫( f ( z + |
zt) − f ( z))dt |
→ 0 , при |
z→0. |
|||||||||
|
|
z |
||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Определение. Функция F(z) такая, что F′(z)=f(z) называется первообразной для f(z) на рассматриваемой области.
Теорема. Любые две первообразные одной и той же функции отличаются на константу.
39

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Логинов А.С. Лекции по ТФКП |
|
Доказательство. Пусть F1(z), F2(z) первообразные для f(z). Положим Φ=F2 - F1. Так как Φ |
||||||||||||||||||||||||||||
голоморфна, то ∂Φ |
= 0 , кроме того, из условия ∂Φ = 0 , следует, что |
∂Φ = 0 , |
∂Φ = 0 откуда и |
||||||||||||||||||||||||||
|
|
|
|
|
∂ z |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
∂x |
∂y |
||||||
следует требуемое утверждение. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z + |
|
|
|
z − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
z |
|
|
|||||||
|
Напоминание. Φ(z)= Φ(x,y)= Φ |
|
|
|
, |
|
|
|
,Φx=ux+ivx, Φy=uy+ivy |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∂Φ = |
∂Φ |
1 |
+ ∂Φ |
1 |
= |
1 |
(Φ |
|
− iΦ |
|
). |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
∂z |
∂x 2 |
∂y 2i |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
∂Φ = |
∂Φ |
1 |
− ∂Φ |
1 |
|
= |
|
1 |
|
(Φ |
|
+ iΦ |
|
). |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x |
y |
|
|
|
|
|
|
|
|
|
|
||||||||||||
∂z |
∂x 2 |
∂y 2i |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
∂Φ = |
∂Φ + |
∂Φ = 0, i |
∂Φ = |
∂Φ − |
∂Φ = 0. |
|
|
|
|
|
|
|
|||||||||||||||||
∂x |
∂z |
∂z |
∂y |
∂z |
∂z |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2.Формула Ньютона-Лейбница |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Теорема. Если F(z) первообразная аналитической функции f(z), то |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ f (ζ )dζ = F (z) − F (z0 ) , |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
в частности, |
F (z) = С + ∫ f (ζ )dζ . |
|
|
|
|
|
|
|
||||||||||||||||||||
a
Доказательство. Если F(z) – первообразная для функции f ( z) , то
z
∫ f (ζ )dζ − F ( z) = С С = −F ( z0 )
z0
Глава 5. Ряды Тейлора и Лорана §1 Ряд Тейлора аналитической функции
Напоминание. Равномерно сходящийся на γ ряд из непрерывных функций можно почленно интегрировать.
1.Теорема Тейлора.
Теорема (Тейлор). Если f аналитическая функция в области D, то для каждой точки z0 D имеет место разложение
∞ |
k |
|
|
|
f (k ) ( z0 ) |
1 |
|
f (ζ ) |
|
|
f ( z) = ∑ak ( z − z0 ) |
|
, | z − z0 |
|< R, ak |
= |
|
= |
|
C∫ |
|
dζ , |
|
|
2πi |
+ |
|||||||
k =0 |
|
|
|
|
k! |
(ζ − z0 )k 1 |
|
|||
R >0 – радиус сходимости ряда, разложение единственно.
Доказательство. Пусть δ меньше, чем расстояние от z0 до границы ∂D.
40
