ТФКП_1_2 / tfkp

Добавил:

Hist Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

Теория функций комплексного переменного

Файл:

при z≠±1, таким образом, эта функция конформна в любой точке кроме

.pdf

Скачиваний:

Добавлен:

11.05.2014

Размер:

1.91 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

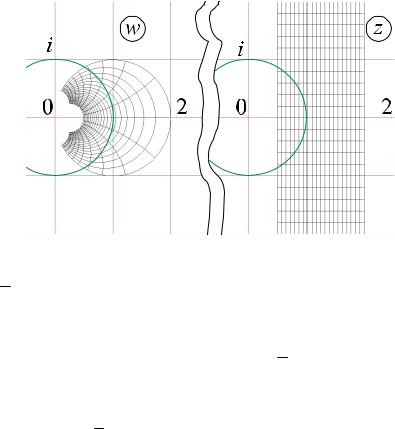
Логинов А.С. Лекции по ТФКП

Так как окружности ортогональны, то отрезок z0 , ζ будет касательной для γ и радиусом для

. По упомянутому свойству касательной, получим равенство |z* - z0||z - z0|=R2, следовательно, точки z0 , z * симметричны относительно .

Пример: Инверсия области D = {z [0.5,2] × [−2,2]} относительно единичной окружности

Доказанная теорема позволяет сформулировать эквивалентное определение симметричных точек для расширенной комплексной плоскости.

Определение. Точки z, z* называются симметричными относительно обобщенной окружности на С , если любая обобщенная окружность, проходящая через эти точки, ортогональна к .

Если обобщенная окружность является прямой, то симметрия точек относительно этой прямой совпадает с симметрией относительно прямой в обычном смысле.

Определение. Отображение z→ z*, переводящее точку z С в симметричную z* относительно , называется симметрией относительно окружности или инверсией. При этом мы считаем, что центр переходит в ∞ , а ∞ в центр окружности.

3.Отображение w = 1 .

Это отображение обладает круговым свойство. Другими словами, образом обычной окружности или прямой может быть только обычная окружность или прямая. Возможно, что окружность перейдет в прямую или наоборот. Действительно, пусть дана окружность в

: Az

z + F

+ E = 0 , подставим в это уравнение z =

, получим

+ F

+ E = 0 или A +

+ Fw + Eww

= 0 или A + Gw + Gw + Eww = 0 , с теме же

условиями на коэффициенты A2 + | G |2 ≠ 0 , E 2 + | G |2 ≠ 0 , A и E вещественные.

Отображение w =

является конформным на расширенной комплексной плоскости ( легко

проверить в 0 и в бесконечности ).

Следствие. Симметрия z* = z0 +

может быть реализована как суперпозиция пяти

z − z0

отображений: сдвиг: w = z − z

, операция сопряжения: w =

, обратная: w =

, растяжение:

w = R2 w , сдвиг:

w = z

+ w и поэтому сохраняет окружности и антиконформна. Под

антиконформностью понимается то, что направление поворота от одной кривой к другой в точке пересечения меняется при отображении на противоположное.

Примеры - иллюстрации:

Логинов А.С. Лекции по ТФКП

w = 1 , z

D: 0.1 ≤ |z| ≤ 1,

0 ≤ arg z ≤ π .

	w =	1

		z − 2
		z − 2

D: 0 ≤

|z| ≤ 1,

0 ≤ arg z ≤ 2π .

4.	Дробно линейная функция.
Дробно линейным называется отображение w =		az + b	a	b
		az + b	. Матрица		называется
			. Матрица		называется
		cz + d	c	d

матрицей дробно линейного отображения. Обычно, мы будем предполагать, что эта матрица не

вырождена

≠ 0 и c ≠ 0 . Дробно линейной отображение не изменится, если матрицу

«пронормировать», т. е. считать, что

= 1 . Это отображение

az + b

(cz + d ) −

−

можно представить в виде суперпозиции простейших

cz + d

c c cz + d

отображений:

w = cz + d , w =

, w = Aw + B .

Из предыдущих свойств следует, что дробно линейное отображение является конформным на расширенной комплексной плоскости и обладает круговым свойством.

Теорема. Свойство сохранения симметричных точек. Дробно линейное отображение L

переводит любые точки z, z*, симметричные относительно окружности на С , в точки w, w*, симметричные относительно образа L( ) этой окружности.

Доказательство. Если z, z* симметричны относительно , то это означает, что все «окружности» γ, проходящие через z, z* , ортогональны . Так как отображение L сохраняет углы и окружности, то любая окружность, проходящая через w, w*, будучи образом некоторой γ, будет ортогональна L( ), что означает симметрию.

Свойства дробно линейных отображений

Логинов А.С. Лекции по ТФКП

1) Дробно линейная функция взаимнооднозначно и конформно отображает всю расширенную комплексную плоскость z на всю расширенную комплексную плоскость w. Обратное отображение так же дробно линейно.

Взамнооднозначность. Разрешим уравнение w =

az + b

относительно z .

cz + d

dw − b

w(cz + d ) = az + b, dw − b = (a − cw)z, z =

. При этом z = ∞ переходит в w =

, а

− cw + a

z = −

переходит в w = ∞ . Если матрица отображения нормирована, то нормирована и матрица

обратного отображения и они взаимно обратны.

Конформность. Производная w' =

a(cz + d ) − c(az + b)

ad − cb

≠ 0 во всех конечных

(cz + d )2

точках, если z ≠ −

. Для проверки конформности в точке z = −

рассматривается функция

cz + d

d 1

c(az + b) − a(cz + d )

cb − ad

= −

, производная которой

≠ 0 в точке z

az + b

(az + b)2

			a	1		+ b
	1	=			ζ

Для проверки конформности в точке z = ∞ рассматривается функция w

	ζ			1
			c			+ d
				ζ

точке ζ = 0

b(c + dζ ) − d (a + bζ )

bc − ad

≠ 0 в точке

. Производная

dζ

(c + dζ )

=a + bζ в c + dζ

ζ= 0 .

2) Суперпозиция двух дробно линейных отображений есть дробно линейное отображение. Матрицы этих отображений при суперпозиции перемножаются: если

w = L(z) =	a11z + a12	, z = M (ζ ) =	b11ζ + b12	, w = L(M (ζ )) =	c11ζ + c12	, тогда
	a21z + a22		b21ζ + b22
					c21ζ + c22

cij = aij bij . Проверяется непосредственно.

3) Круговое свойство и сохранение симметрии. Произвольное дробно линейное отображение L обладает круговым свойством и переводит любые точки z, z*, симметричные относительно какой-

нибудь окружности γ на С , в точки w, w*, симметричные относительно образа =L(γ) этой окружности.

4) Каковы бы ни были три различные точки z1, z2, z3 C и три различные точки w1, w2, w3 C, существует единственное дробно линейное отображение L такое, что L(zk)=wk, k=1,2,3.

Доказательство. Рассмотрим отображение ζ = L 1(z) , переводящее точки z1, z2, z3 в 0, ∞, 1 ,

L : ζ =

z − z1

z3 − z2

, z1→0, z2→∞, z3→1. Аналогично, отображение ζ = L

(w)

z − z2

z3 − z1

L : ζ =

w − w1

w3 − w2

, будет переводить w1→0, w2→∞, w3→1 Тогда отображение

w − w2

w3 − w1

w = L(z) = L−1

(L (z)) = L−1 o L будет искомым : L(zk)=wk, k=1,2,3.

Для доказательства единственности, докажем лемму.

Логинов А.С. Лекции по ТФКП

Лемма. Если дробно линейное отображение переводит точки 0→0, ∞→∞, 1→1, то оно тождественное.

Доказательство. Из 0→0 b=0, ( при этом можно считать, что a=1 ) таким образом,

отображение должно иметь вид w =

. ∞→∞ c=0, w =

,1→1 w = z .

cz + d

Докажем единственность. Предположим, что ещё одна дробно линейная функция w=f(z)

обладает этим свойством. Тогда g = L o f o L−1

оставляет на месте 0,∞,1. Такое отображение

является тождественным I = L o f o L−1 , откуда следует, что f = L−1

o L = L .

5) Непосредственной проверкой можно убедиться, что

w1 − w3

w1 − w4

z1 − z3

z1 − z4

, w = L(z

) .

w2 − w3 w2 − w4 z2 − z3

z2 − z4

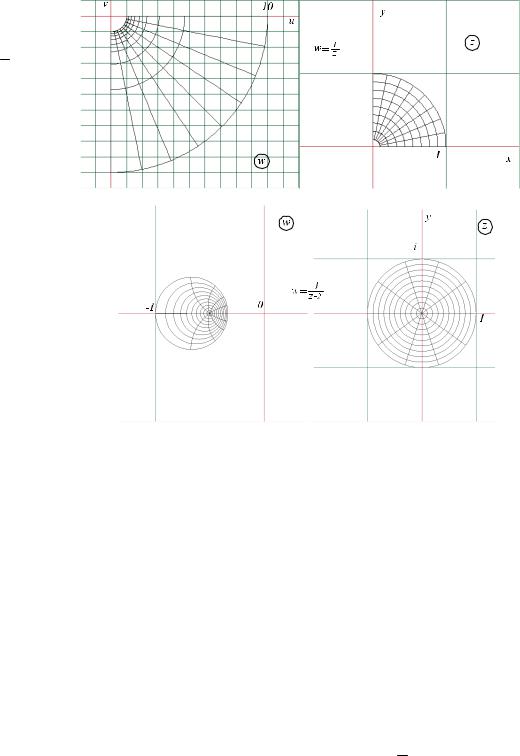
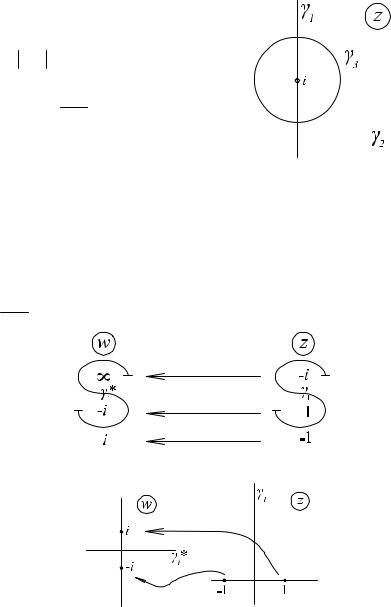
Пример. Найти образы обобщенных окружностей

γ1,γ 2 ,γ 3 : z − i = 1, вещественная и мнимая оси при отображении

= z − i w z + i .

Замечание. Обобщенная окружность является прямой только тогда, когда она проходит через точку ∞ , в противном случае она является обычной окружностью.

В∞ отображается точка − i , которая принадлежит “окружности” γ1 . Это значит, что только

γ1 * является прямой, а γ 2 * , γ 3 * будут обычными окружностями. Для того, чтобы нарисовать

прямую γ1 * возьмем любые две симметричные относительно “окружности” γ1 точки z1 , z2 ,

например, -1, 1. Эти точки перейдут в симметричные точки z1*, z2 * относительно γ1 * . Подставляя

= z − i

значения -1, 1 в w z + i найдем образы этих точек − i,i .

Рисуем прямую γ1 * , для которой эти точки являются симметричными

Для изображения окружностей γ 2 * , γ 3 * нужно найти их центры и точки, через которые они будут проходить. Для нахождения центра окружности γ 2 * найдем точку симметричную ∞ .

Логинов А.С. Лекции по ТФКП

Центром окружности γ 2 * будет точка 0 . Так как все три кривые пересекаются в 0, а 0

переходит в -1, то γ 2 * будет окружностью радиуса 1.

Тоже самое для окружности γ 3 * . Находим, кто симметричен прообразу ∞ .

Точку	i	, симметричную − i относительно окружности γ		находим из соотношения
			3
2

инверсии.

§2 Степенная функция w=zn, n - натуральное.

1.Отображение степенной функцией.

w=zn=rneinϕ. Область однолистности: для того, чтобы условие однолистности нарушалось в области D, в этой области должна существовать пара различных точек z1 ≠ z2 , для которых образы

совпадают: zn = zn		. В этом случае \|z1\|=\|z2\| и n arg z1 = n arg z2 + 2πk, arg z					− arg z		=	2πk	.
совпадают: zn = zn							− arg z	2	=		.
1	2					1		2		n
										n
Поэтому, если в какой-либо области для различный точек z1 ≠ z2 будет выполнено
соотношение arg z		− arg z		<	2π	, то однолистность нарушаться не будет. В частности, каждую из
соотношение arg z		− arg z	2	<
	1		2		n
					n

								Логинов А.С. Лекции по ТФКП
областей D :	2kπ	< arg z <		2(k + 1)π	функция w=zn отображает однолистно на плоскость с вырезом
областей D :		< arg z <			функция w=zn отображает однолистно на плоскость с вырезом
k	n			n
	n			n
по положительной части действительной оси.
					4π		6π
Пример: w = z5			. Выбрана область \| z \|> 0.1, arg z			,
Пример: w = z5			. Выбрана область \| z \|> 0.1, arg z			,
					5	5

2.Обратная функция.

Определение. Функция f(z) называется однозначной ветвью на множестве D многозначной

функции F(z), определённой на D, если f(z) однозначная, непрерывная функция, совпадающая с одним

из значений F(z) в каждой точке z D.

Пример: Обратная функция z = n

w многозначна ( n различных корней, если w≠0 )

z = n | w |e

i arg w + 2πk

. Рассмотрим n экземпляров плоскости Cw с разрезом по положительной

части вещественной оси, будем их обозначать D*k , k =0,1,…, n - 1. Определим одну из возможных

ветвей. Зафиксируем некоторую точку wk D*k и для её образа выбираем значение

arg wk

+ 2πk

arg wk

2πk

= n

| w |e

= n | w |e

n e n .

Значение ветви gk(w) в любой точке w D*k будем определять следующим образом: положим

z = n | w |e

i Argw

i 2πk

n e

n , где Arg w получен из arg wk непрерывным изменением вдоль какой-либо

кривой, соединяющей w и wk. Можно показать, что конечное значение arg w не будет зависеть от

конфигурации пути, поэтому определение корректно.

В данном случае (удачный выбор областей Dk * ) можно было бы не прибегать к услугам

кривой γ , а считать выражение z = n | w |e

i arg w

i 2πk

n e

n за определение k-ой ветви. Таким образом, можно

выделить n однозначных ветвей для функции n

w . Обозначают эти ветви (n w )k . Ветвь,

соответствующая k, есть конформное отображение области D*k на область

2πk

< arg z <

2π (k + 1)

Логинов А.С. Лекции по ТФКП

Замечание. При отображении z = w* = n w , в плоскости w при полном обходе вокруг начала координат arg w получает приращение 2π и мы приходим к другому значению w* в плоскости z , w1* = n w, w2 * = n w, w1* ≠ w2 * .

Такие точки называются точками ветвления, точное определение точки ветвления будет дано в следующем пункте. Для степенной функции, кроме 0, точкой ветвления является ∞.

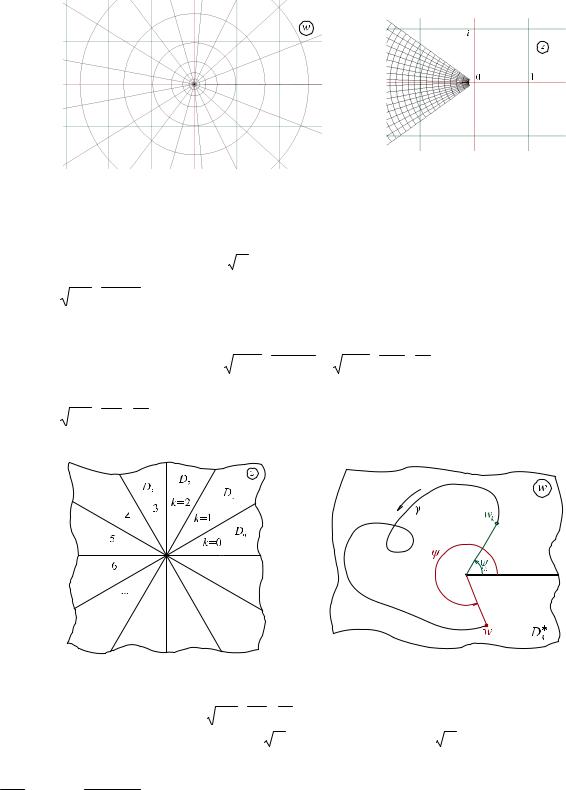
3. Понятие римановой поверхности для функции z =	w
Два листа D0 , D1 склеены, как показано на рисунке. При обходе точкой w по 0 по
верхнему листу D*0 образ z пройдет пол-оборота по кривой γ0	в верхней полуплоскости D0

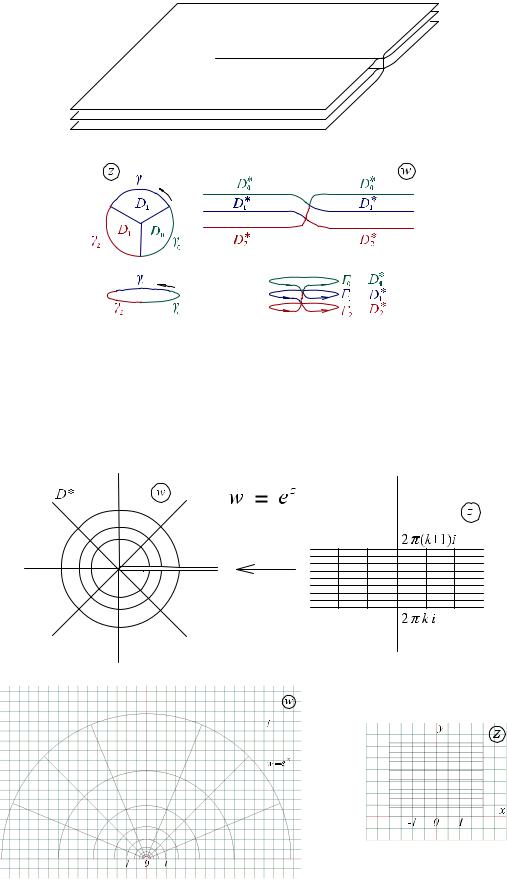
плоскости z. Продолжаем движение, переходим в месте склейки с верхнего листа D*0 на нижний лист D*1 на кривую 1 в плоскости w. Далее образ z будет двигаться по γ1 в нижней полуплоскости D1 плоскости z и полностью завершит оборот, когда точка w вернется на верхний лист D*0 по кривой1 . Поверхность D*0 D*1 взаимнооднозначно отображается на всю плоскость Cz . Эта поверхность D*0 D*1 называется поверхностью Римана.

Определение. Если в любой достаточно малой окрестности точки a С существует замкнутая Жорданова кривая γ (можно считать окружность с центром a), содержащая внутри точку a такая, что при обходе γ, начиная с точки z0 γ ( и непрерывном изменении модуля и аргумента ) значение ветви fk (z0) многозначной функции F(z) переходит в значение другой ветви f1 (z0 ) , то точка a называется точкой ветвления.

Пример. Поверхность Римана для z = 3 w .

Логинов А.С. Лекции по ТФКП

§3 Функция w=ez

1.Отображение w = ez .

w=u+iv=exeiy, |w|=ex, arg w = y

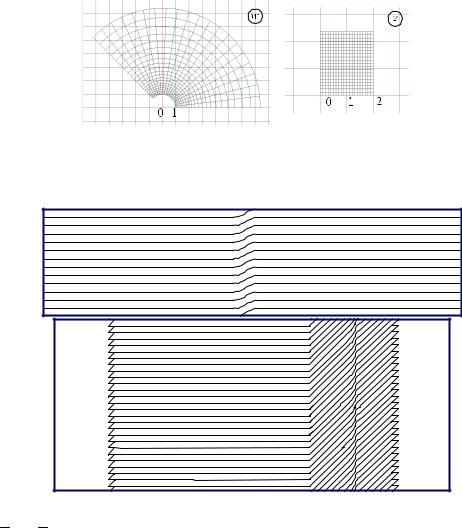
Нарушение условия однолистности: z1 ≠ z2 , в то время, как ez1 = ez2 , или x1=x2, y1=y2+2πk,

поэтому в областях вида Dk={z:2πk < Im z < 2π(k+1) } однолистность нарушаться не может. Каждая из таких областей однолистно отображается на плоскость с разрезом по положительной части вещественной оси.

Пример. w = ez , z [−2,2] × [0,π ]

Логинов А.С. Лекции по ТФКП

Пример: D = [0,2]× 0,	3	π	, w = ez

	4

2.Обратная функция.

Если w=ez, то |w|=ex, x=ln |w|, arg w = y откуда для обратной функции z = Ln w = ln|w|+i Arg w = ln|w|+i (arg w + 2πk ). При k=0 получаем ln w. Для z = Ln w поверхность Римана набирается из счетного числа листов, имеющих разрез по положительной части вещественной оси и склеиваемых друг с другом последовательно.

§4 Функция Жуковского

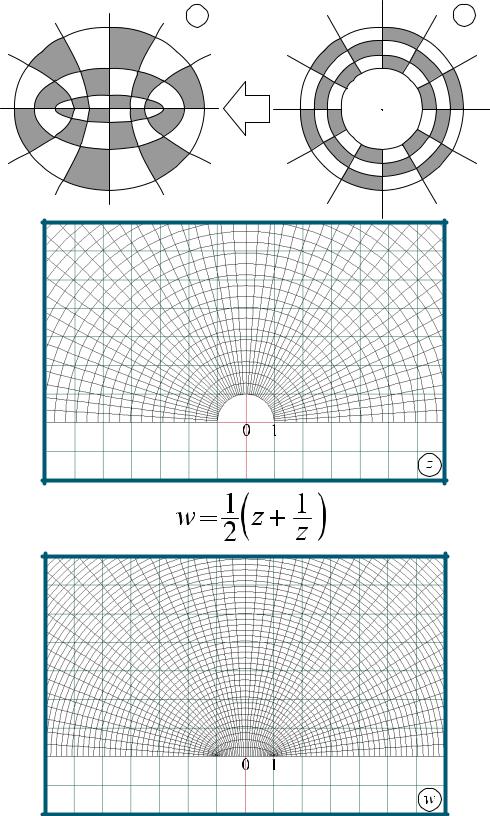
w = 1 ( z + 1 ) Определена, однозначна и аналитична всюду в C кроме z=0.

z = ±1, ( конформность в 0 и в ∞ проверить самостоятельно )																																	z1 − z2
		Нарушение однолистности.										z ≠ z					, z +				1	= z				+		1		, z − z		=	z1 − z2			1 −	1	= 0 ,
												z ≠ z				2	, z +					= z			2	+				, z − z	2	=					1
													1			2		1			z1				2			z2		1	2		z1 z2				z1z2
																					z1							z2					z1 z2				z1z2
откуда следует, что однолистность нарушается в точках																									z1, z2 ,					z1 ≠ z2 : z1z2=1. Областью
однолистности является, например, каждое из следующих множеств \|z\|<1, \|z\|>1, Im z > 0 .
		Пусть z=r ( cos ϕ + i sin ϕ ) = r eiϕ, тогда w = u + iv =																									1							cosϕ − i sin ϕ
																													r cosϕ + ir sin ϕ +										,
																													r cosϕ + ir sin ϕ +										,
																											2										r
								1			1								1				1
						u =			r +			cosϕ,					v =			r		−		sin ϕ											(1)
						u =			r +			cosϕ,					v =			r		−		sin ϕ											(1)
								2			r								2				r
		Следовательно, окружность r=r0 переходит в эллипс с полуосями
a =	1		1		1		−	1		2	= a		2	− b	2	=		1		= 1 . Фокусы в точках c = ± 1.
	1		1		1			1		2			2		2			1	4

	2	r0 +		,b =	2	r0			, c									4
	2		r0		2			r0										4

					Логинов А.С. Лекции по ТФКП
Из (1) следует, что лучи arg z = α переходят в гиперболы	u2	−	v2		= 1 с фокусами ±1.
Из (1) следует, что лучи arg z = α переходят в гиперболы	cos2 α	−	sin2	α	= 1 с фокусами ±1.
	cos2 α		sin2	α

Асимптоты гипербол v = ±u tgα . Функция Жуковского переводит внешность единичного круга на плоскость с разрезом по отрезку [-1,1].

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Соседние файлы в папке ТФКП_1_2

#
11.05.20141.91 Mб54tfkp.pdf
#
11.05.2014255.18 Кб55tfkp2.pdf