
ТФКП_1_2 / tfkp
.pdf
Логинов А.С. Лекции по ТФКП
Глава 1. Основные понятия
§1 Операции над комплексными числами
Комплексные числа и операции над комплексными числами изучались на первом семестре. Основные понятия, связанные с комплексными числами: алгебраическая форма записи комплексного числа, операции над комплексными числами, вещественная (действительная) и мнимая части ,
Re z, Im z , сопряжённые числа и следующие их свойства
z1 z2 = z1 z2 , z1 + z2 = z1 + z2 .
Формула Бинома Ньютона: для любых комплексных чисел a,b и натурального n справедливо
n |
n! |
|
|
|
равенство (a + b)n = ∑ |
ak bn − k . |
|||
k!(n − k)! |
||||
k =0 |
|
|||
Аргумент и модуль комплексного числа z=x+iy,
|z|= r = 
 x2 + y2 , главное значение аргумента: ϕ=arg z, arg z [0,2π ), Arg φ = arg φ+2πk .
x2 + y2 , главное значение аргумента: ϕ=arg z, arg z [0,2π ), Arg φ = arg φ+2πk .
Tригонометрическая форма записи комплексного числа: z=reiϕ =r ( cos φ +i sin φ ). Расстояние между комплексными числами ρ (z1,z2)=| z1 - z2|
Пример: Множество {z − i + z + 1 = 2} представляет собой геометрическое место комплексных чисел, сумма расстояний которых до i и -1 равна 2. Эллипс с фокусами в i и -1.
Возведение в степень, формула Муавра: если z=reiϕ , то zn=rneinϕ =rn( cos nφ +i sin nφ ).
Извлечение корней: если wn=z, то w = n  z ,| w |= n | z |, arg w = arg z + 2πk , k = 0,1,..., n − 1. n
z ,| w |= n | z |, arg w = arg z + 2πk , k = 0,1,..., n − 1. n
Здесь под n  | z | понимается арифметическое значение корня.
| z | понимается арифметическое значение корня.
§2 Комплексная плоскость
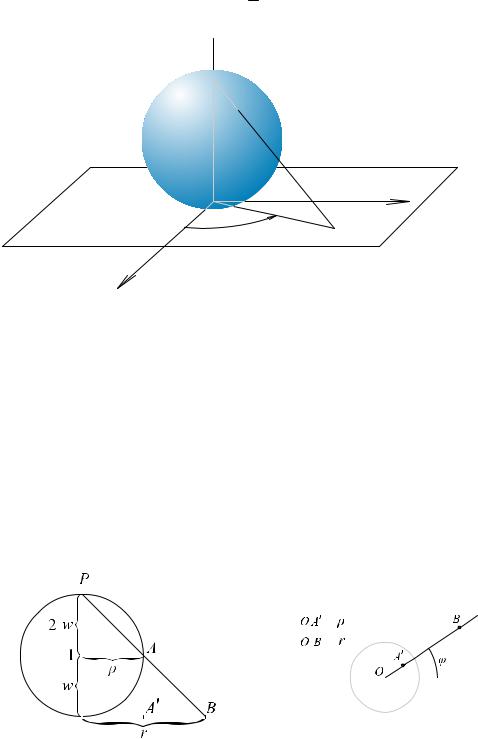
Множество комплексных чисел удобно интерпретировать как плоскость, которую называют комплексной плоскостью и обозначают C, комплексное число – это точка на этой плоскости. Можно рассматривать комплексное число, как радиус вектор. В последнем случае операции сложения комплексных чисел совпадают с операциями сложения векторов. Комплексная плоскость С с добавленной к ней несобственной «бесконечно удаленной точкой» ∞ называется расширенной
комплексной плоскостью и обозначается C . Геометрически бесконечно удаленную точку можно интерпретировать с помощью сферы Римана.
1
Логинов А.С. Лекции по ТФКП
Рассмотрим сферу S, касающуюся комплексной плоскости в точке (0,0). Между точками
сферы S и точками расширенной комплексной плоскости C устанавливается взаимнооднозначное соответствие, как показано на рисунке.
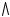 w
w
P 
A=(u,v,w)
y,v
ϕ
B=(x,y)
u,x
Стереографическая проекция (сфера Римана)
Именно, из верхнего полюса сферы проводится луч, соединяющий точку сферы A с некоторой точкой B плоскости. Самому полюсу P соответствует бесконечно удаленная точка ∞. Эта сфера называется сферой Римана. Это отображение для случая сферы радиуса 1 задается следующими функциями:
|
|
|
|
|
|
|
|
z = x + iy = |
u + iv |
. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 − w |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u = ρ cosϕ |
|
Для доказательства, рассмотрим полярные координаты (см. рисунок): |
|
тогда |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v = ρ sin ϕ |
|
x = r cosϕ |
|
|
|
|
|
|
x = r cosϕ = |
|
|
ρ |
cosϕ = |
|
u |
|
|
|
|||||||||
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
, |
|
= r , откуда получим: |
2 |
− w |
|
|
|
|
2 − w . |
|
|
||||||||||||||
|
|
|
|
||||||||||||||||||||||
y = r sin ϕ |
2 − w |
|
|
|
|
|
y = r sin ϕ = |
|
ρ |
sin ϕ = |
|
v |
|
|
|
||||||||||
|
|
|
|
|
|
− w |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
2 |
2 |
− w |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Можно показать, что прямые и окружности из C переходят в окружности на S, а углы между пересекающимися кривыми сохраняются.
С точки зрения расстояния, введенного для комплексных чисел, комплексная плоскость представляет собой евклидово пространство. Таким образом, для комплексных чисел используются те же определения и справедливы те же теоремы, связанные со сходимостью в этом пространстве:
Окрестность точки z0: Uε(z0)= {|z - z0|<ε }.
Окрестность бесконечно удалённой точки : U(∞)={|z|>R} .
2
|
|
|
Логинов А.С. Лекции по ТФКП |
o |
|
|
|
Проколотая окрестность : U ε (z0 ) = {0<|z - z0|<ε }. |
|
|
|
Сходимость, предел последовательности: z0 = lim zn |
означает, что lim | zn − z0 |= 0 |
||
n →∞ |
n |
→∞ |
|
Необходимое и достаточное условие сходимости для случая, когда z |
0 |
C |
|
|
|
|
|
zn → z0 xn → x0 , yn → y0
Критерий Коши сходимости последовательности к конечному пределу (в С) :
ε Ν n>Ν m>Ν: zn - zm < ε .
Множество комплексных чисел является линейным пространством. Наличие метрики и операций линейного пространства позволяет ввести такое понятие, как числовой ряд. Комплексный
∞ |
∞ |
∞ |
∞ |
ряд ∑zk с общим членом zk = xk + iyk определяется, как ∑zk |
= ∑xk |
+ i∑ yk . В случае |
|
k =0 |
k =0 |
k =0 |
k =0 |
∞ |
∞ |
|
|
сходимости обоих действительных рядов ∑xk , ∑ yk получаем комплексное число – сумму этого |
|||
k =0 |
k =0 |
|
|
ряда. Таким образом, изучение комплексного ряда сводится к изучению двух вещественных рядов. Наиболее важными свойствами рядов, используемых в дальнейшем, являются: абсолютная сходимость, свойства суммы, разности рядов, перестановка и перемножение абсолютно сходящихся рядов.
§3 Некоторые понятия, относящиеся ко множествам. Кривые.
Диаметр множества M : dM = sup | z1 − z2 | . |
|
|
|
z1 , z2 M |
|
|
|
«Расстояние» между множествами M1, M2 : ρ (M1 |
, M 2 ) = |
inf |
| z1 − z2 | . В точном |
|
z1 |
M1 , z 2 |
M 2 |
смысле, это расстоянием не является, так как не выполняется первое свойство или аксиома расстояния.
Предельная точка множества – точка, в любой проколотой окрестности которой есть хотя бы одна точка множества.
Замкнутое множество – множество, содержащее все свои предельные точки. Внутренняя точка множества – точка, принадлежащая множеству вместе с некоторой своей окрестностью, открытое множество – множество, каждая точка которого внутренняя.
Граничная точка множества – любая окрестность точки содержит, как точки из множества, так и точки из его дополнения. Граница множества D (множество всех граничных точек) обозначается ∂D, она всегда замкнута.
Кривая z=z(t)=x(t)+iy(t), t [α,β] . На плоскости этому соответствует параметрическое задание
x= x(t)
=, t [α , β ] . y y(t)
Ориентация кривой или направление обхода, непрерывная кривая: x(t), y(t) обе непрерывны.
Непрерывная кривая называется простой или кривой Жордана, если различным значениям t1, t2 (кроме может быть α и β ) соответствуют различные точки z(t1), z(t2) на комплексной плоскости (у кривой нет самопересечений).
Кривая замкнута, если z(α)=z(β) (не путать с замкнутостью в смысле теории множеств ). Связное множество. Любые две точки этого множества можно соединить простой кривой,
лежащей в этом множестве.
Областью, если не оговорено что-либо другое, будем называть связное открытое множество. Множество D C называется n - связным, если ∂ D состоит из n связных, попарно
непересекающихся компонент. Иногда используется термин: n - связная область.
Кривая называется гладкой, если x(t), y(t) и их производные непрерывны и z′(t)=x′(t)+i y′(t)≠ 0. Если кривая замкнута, то дополнительно требуется z′(α)=z′(β) ( точнее z′(α+0)=z′(β - 0) ).
Кусочно-гладкая кривая. Непрерывная кривая, состоящая из конечного числа гладких кусков.
3
Логинов А.С. Лекции по ТФКП
§4 Функции комплексного переменного
Определение. w = f (z), z D. Каждому z ставится в соответствие одно или несколько значений w. Множество всевозможных значений f (z) называется областью значений функции f . Если сопоставляемое значение единственно, то функция называется однозначной и в этом случае говорят об однозначном отображении D на .
Примеры:
w= z2, z C, однозначная функция.
w= n  z является многозначной функцией.
z является многозначной функцией.
Определение логарифмической функции (большой логарифм): w = Ln z = ln r + i (ϕ + 2πk ), r=|z|, ϕ = arg z [ 0 , 2π ) , k-целое, D = C\0. Функция Ln z является многозначной функцией.
Главная ветвь логарифма (маленький логарифм): w = ln z = ln r + i ϕ, r=|z|, ϕ = arg z [0,2π ), D = C\{0}. Функция ln z является однозначной функцией.
Пример: ln(-1)= iπ .
w = Arg z = arg z + 2πk, (k-любой целое) многозначная функция.
Степенная функция: w = zb определяется по формуле zb = eb Ln z . Она может быть для некоторых b многозначной ( для натуральных b определение согласуется с операцией возведения в степень путём перемножения ).
Пример: (−1)π = eπ Ln( −1) |
= eπ i (π + 2π k ) = cos(π 2 (1 + 2k )) + i sin(π 2 (1 + 2k )) . Таким образом, |
|
числу -1 соответствует бесконечное число (счетное) значений функции w = zπ . |
|
|
Если функция f(z) однозначная, то можно определить обратную функцию |
f −1 . Для этого |
|
обозначим через D область определения функции f(z), а область ее значений через |
. Обратная |
|
функция f -1 будет определена на |
и каждому значению w из будет сопоставлять все те значения z |
|
из D для которых f(z)=w. Обратная функция не обязана быть однозначной.
Если f и f -1 однозначные, то отображение z → w = f(z) называется однолистным (взаимнооднозначное отображение).
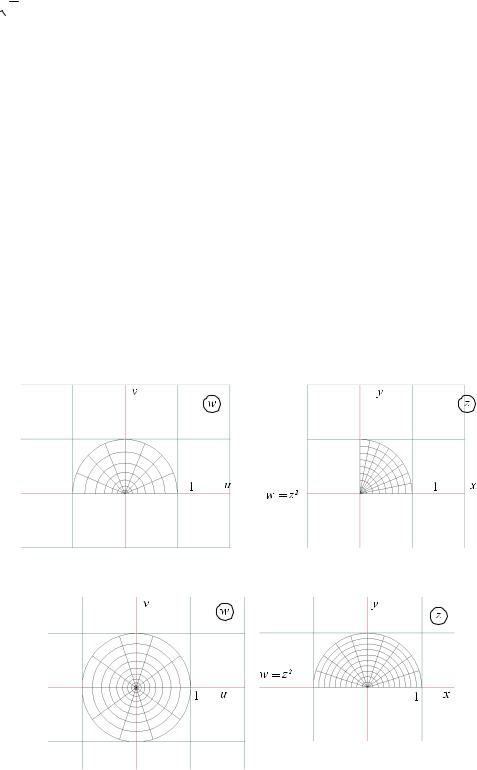
Пример: функция w=z2 отображает однолистно область D={|z|<1,0< arg z < π } на верхний
2
полукруг
Пример: функция w=z2 отображает однолистно область D={|z|<1, 0< arg z < π } на круг радиуса 1 с вырезом по положительной части вещественной оси
4
Логинов А.С. Лекции по ТФКП
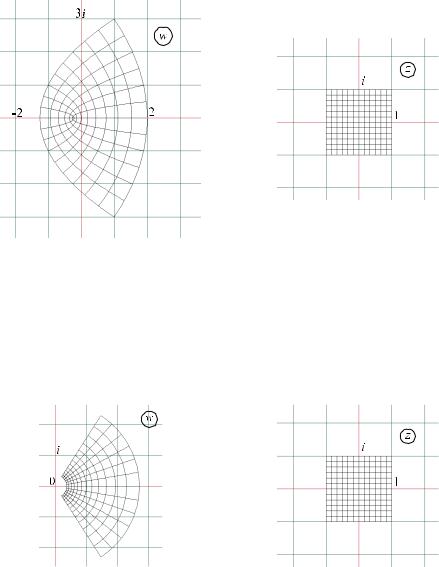
Пример: Найти образы линий прямоугольной сетки квадрата [-1,1] × [-1,1] при отображении w=z2+z. Отображение имеет вид
|
|
|
|
|
|
|
|
|
|
u = x − y + x |
||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
v = 2xy + y |
|||
Вертикали x = c переходят в параболы : |
|
|
|
|||||||||||
u = c2 − y2 + c |
|
|
|
|
v 2 |
|
|
|
|
|
|
|||
, u = c2 + c − |
|
|
|
направленными направо. Горизонтали y=c переходят в |
||||||||||
|
|
|||||||||||||
v = (2c + 1) y |
|
|
|
2c + 1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
параболы u = x |
2 |
− c |
2 |
+ x ,u = |
v − c |
|
2 |
v − c |
|
|
|
|
||
|
|
|
+ |
− c2 |
направленными налево. |
|||||||||
|
|
|
|
|
||||||||||
v = 2xc + c |
2c |
2c |
|
|
|
|||||||||
Пример: Найти образы линий прямоугольной сетки квадрата [-1,1] × [-1,1] при отображении w=ez. Для z = x + iy получим w = u + iv = exeiy = ex cos y + iex sin y . Таким образом, это отображение можно представить в виде:
u= ex cos y v = ex sin y .
Прямоугольная сетка переходит в полярную сетку (лучи и окружности)
Пример: Найти образы линий прямоугольной сетки квадрата [-1,1] × [-1,1] при отображении w = ez 2 . Расписывая действительную и мнимую части, отображение можно записать в виде:
u = e |
x 2 |
− y 2 |
|
||
|
|
|
|
cos(2xy) |
|
v = e |
x |
2 |
− y |
2 |
. |
|
|
|
|||
|
|
|
|
||
|
|
|
|
sin(2xy) |
|
Образы координатной сетки показаны на рисунке.
5
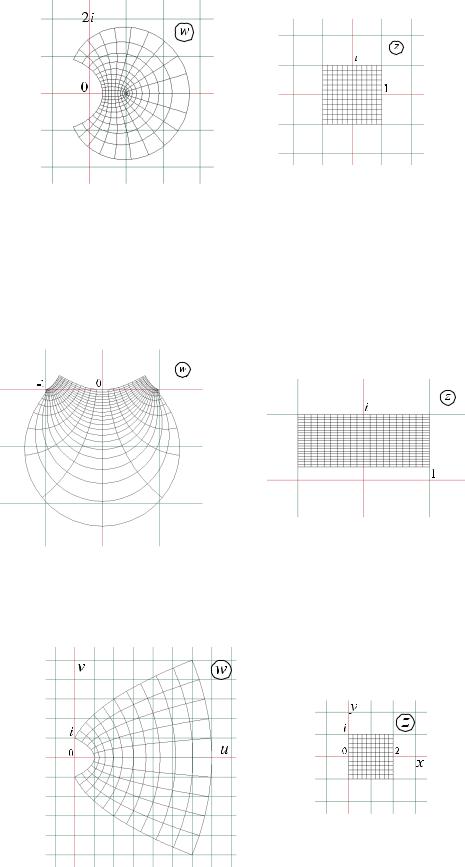
Логинов А.С. Лекции по ТФКП
|
|
|
Пример: Найти образы линий прямоугольной сетки квадрата [-1,1] × [0.2,1] при отображении |
||||||||||||||
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
w = |
|
z + |
|
. Отображение имеет вид |
|
|
|
|
|
|
|
|
|
|
|||
2 |
z |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
u = |
x |
|
|
+ |
|
|
|
1 |
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
+ y |
2 |
|||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
1 |
|
|
. |
|
|
|
|
|
|
v = |
|
1 |
− |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ y |
2 |
|
||
|
|
|
|
|
|
|
2 |
|
|
x |
|
|
|
||||
Пример: Найти образы линий прямоугольной сетки квадрата [0,2] × [-1,1] при отображении w = 1 + z + z2 . Отображение имеет вид
u = 1 + x + x |
|
− y |
. |
|
2 |
|
2 |
v = y + 2xy |
|
||
6
Логинов А.С. Лекции по ТФКП
При исследовании многозначных функций выделяют однозначные ветви. Понятие
однозначной ветви многозначной функции рассмотрим на примере. У функции w = 
 z в качестве области определения D возьмём всю комплексную плоскость с вырезом по положительной части действительной оси, x [0,∞).
z в качестве области определения D возьмём всю комплексную плоскость с вырезом по положительной части действительной оси, x [0,∞).
В этой области рассмотрим функции
w = f (z) = |
|
i ϕ |
|
(z) = |
|
i ( ϕ +π ) |
|
|
|
||||
re 2 , w = f |
2 |
re 2 , r =| z |,ϕ = arg z (в области D главное значение аргумента z |
||||
1 |
|
|
|
|
|
|
будет лежать в диапазоне 0 < arg z < 2π ). Эти функции представляют собой однозначные ветви исходной функции в области D. Первая однолистно отображает область D на верхнюю полуплоскость, вторая функция однолистно отображает область D на нижнюю полуплоскость. Однозначные ветви можно выделять различными способами. Точное определение однозначной ветви будет дано позже.
Определение предела и непрерывность По Коши: z0 C ,
lim f (z) = A : ε > 0 δ > 0 z, 0 < z – z0< δ : f(z) - A< ε |
||||||||
z → z0 |
|
|
|
|
|
|
|
|
lim f (z) = ∞ : R |
δ > 0 z, 0 < z – z0 < δ : | f(z)| > R |
|||||||
z → z0 |
|
|
|
|
|
|
|
|
lim f (z) = A : ε > 0 r |
z, z > r |
: f(z) - A< ε |
||||||
z →∞ |
|
|
|
|
|
|
|
|
lim f (z) = ∞ : R |
r |
z, z > r |
: | f(z)| > R |
|||||
z →∞ |
|
|
|
|
|
|
|
|
Аналогично дается определение по Гейне: {zn}, zn ≠ z0 , zn → z0 : lim f (zn ) = A . |
||||||||
|
|
|
|
|
|
n →∞ |
||
Замечание: Существование конечного предела lim f (z) эквивалентно существованию двух |
||||||||
|
|
|
|
|
|
z → z0 |
||
пределов lim Re f (z), lim Im f (z) . |
|
|
|
|
|
|
||
z → z0 |
z → z0 |
|
|
|
|
|
|
|
Так, если |
f (z) = u(z) + iv(z) → A = a + ib при z → z0 , то u(z) → a, v(z) → b , при z → z0 . |
|||||||
Непрерывность функции f(z) в точке z |
0 |
C : |
lim f (z) =f(z0), предполагается, что функция |
|||||
|
|
|
|
|
z → z0 |
|||
|
|
|
|
|
|
|||
определена в некоторой окрестности точки z0 . |
|
|
|
|
||||
В терминах расширенной комплексной плоскости: f ( z) непрерывна в z0 |
|
, w0 = f (z0 ) , |
||||||
C |
||||||||
если для любой окрестности U (w0 ) |
найдется окрестность U (z0 ) такая, что из z U (z0 ) следует |
|||||||
f (z) U (w0 ) .
Замечание: Если f(z0)≠∞, то непрерывность в этой точке эквивалентна непрерывности действительной и мнимой части в этой точке.
1 |
|
|
≠ |
|
|
||
|
|
|
, |
z |
0 |
|
|
|
|
||||||
Пример: Функция f (z) = z |
= |
является непрерывной в точке z=0 в смысле |
|||||
∞ |
|
|
|
|
|||
|
, |
z |
|
0 |
|
||
расширенной комплексной плоскости.
7

Логинов А.С. Лекции по ТФКП
§5 Функциональные последовательности и ряды
|
|
∞ |
Если fn(z) - однозначные функции , то комплексный ряд ∑ fk ( z) определяется, как сумма |
||
|
|
k =0 |
∞ |
∞ |
∞ |
∑ fk ( z) = ∑Re fk (z) + i∑Im fk (z) . |
||
k =0 |
k =0 |
k =0 |
Ряд называется равномерно сходящимся на D, если его частичные суммы
n
Sn (z) = ∑ fk (z) равномерно сходятся на D к некоторой функции S(z), т. е.
k =0
ε > 0 Ν n > Ν z D: Sn (z) − S (z) < ε .
Критерий Коши: ε > 0 Ν n > Ν m , m ≥ 0 z D: |
Следствие (Необходимое условие сходимости). Если ряд
n + m
∑ fk ( z) | < ε.
k= n
∞
∑fk ( z) сходится в точке z , то
k=0
общий член этого ряда fk (z) стремится к нулю в этой точке.
Аналогичное утверждение можно сформулировать для равномерной сходимости:
∞
Если ряд ∑ fk ( z) равномерно сходится на D , то общий член этого ряда fk (z) равномерно
k =0
стремится к нулю на D.
Достаточный признак Вейерштрасса:
Если fk(z) ≤ αk, z D и числовой вещественный ряд ∑αk сходится, то ряд ∑ fk(z) сходится на D равномерно.
Полезная теорема. Сумма равномерно сходящегося ряда из непрерывных функций (равномерная сходимость на компакте), есть функция непрерывная.
|
|
|
§6 Степенные ряды |
|||||||||
1. |
Основные свойства степенных рядов. |
|
|
|
|
|
|
|
||||
Напоминание: Признаки Даламбера и Коши для положительных рядов ( вещественных ) |
||||||||||||
∑ak , 0 ≤ ak . |
|
|
|
|
|
|
|
|
||||
|
|
|
|
∞ |
|
|
|
|
an +1 |
|
||
Даламбер: Если для положительного ряда ∑ak , ak > 0 существует предел lim |
= q , то |
|||||||||||
|
|
|||||||||||
|
|
|
|
k = 0 |
|
|
n →∞ an |
|||||
при q < 1, ряд сходится, при q > 1, расходится. |
|
|
|
|
|
|
|
|||||
|
|
|
= lim sup bk . |
|
|
|
|
|
|
|
||
Определение верхнего предела lim bn |
|
|
|
|
|
|
|
|||||
|
n →∞ |
n→∞ k > n |
|
|
|
|
|
|
|
|||
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
Коши: Если для положительного ряда ∑ak , ak ≥ 0 существует предел |
lim |
n |
| an | |
= q , то |
||||||||
|
|
|
|
k =0 |
n→∞ |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
при q < 1, ряд сходится, при q > 1, расходится. |
|
|
|
|
|
|
|
|||||
Комплексные степенные ряды: |
|
|
|
|
|
|
|
|
||||
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
∑ck ( z − z0 )k |
или |
|||||||
|
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
∑ck z k |
(1) |
|
|
|
|
|
|
||
k =0
Теорема 1 (Первая теорема Абеля ) Если ряд (1) сходится в точке z0 ≠ 0, то он сходится абсолютно в круге |z| < |z0|.
8

Логинов А.С. Лекции по ТФКП
∞
Доказательство: Ряд ∑ck z0k сходится, следовательно, согласно необходимому условию
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сходимости ряда, будет выполнено c zk → 0 , откуда следует, что B k :| c |
k |
z k |< B . Поэтому для |
|||||||||||||||||||
k 0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
z k |
|
z |
|
|
k |
|
|
|
|
|
< |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
= |
c |
|
z k |
< B |
|
|
= Bqk , q < 1, при |
|
z |
|
|
z |
|
|
||||||
общего члена ряда (1) можно выписать оценку: |
c zk |
|
|
|
|
|
|
|
. |
||||||||||||
|
|
|
|
||||||||||||||||||
|
k |
|
|
k |
0 z0k |
|
z0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∞
Таким образом, ряд из модулей исходного ряда мажорируется сходящимся рядом ∑Bqk в каждой
k =0
точке круга {| z |<| z0 |} .
Следствие 1. Для любого степенного ряда (1) существует число R (0 ≤ R ≤ ∞) такое, что при |z|<R ряд сходится, при |z|>R ряд расходится. Это число называется радиусом сходимости степенного ряда. Круг {|z| < R} называется кругом сходимости.
Следствие 2. Радиус сходимости комплексного степенного ряда (1) совпадает с радиусом
∞ |
|
сходимости вещественного степенного ряда ∑| ck | xk . |
|
k =0 |
|
∞ |
∞ |
Для этого утверждения необходимо сначала показать, что ряд ∑ck z k (1) и |
∑| ck | z k (2) |
k =0 |
k =0 |
имеют один и тот же радиус сходимости.
Действительно, пусть их круги сходимости имеют радиусы R1, R2. Во всех точках |z|<R1 ряд
(1)сходится абсолютно и, следовательно, (2) тоже сходится абсолютно, т.к. ряды из модулей для (1) и
(2)одинаковы. По этой же причине справедливо обратное утверждение, во всех точках |z|<R2 будет
∞
сходится абсолютно не только ряд (2), но и ряд (1). После этого можно рассмотреть ряды ∑| ck | z k
k =0
∞
и ∑| ck | xk и показать, что они имеют один и тот же радиус сходимости, используя первую теорему
k =0
Абеля.
В частности, справедливо
Следствие 3. Комплексный ряд с вещественными коэффициентами имеет тот же радиус сходимости, что и вещественный ряд с этими коэффициентами.
Теорема 2 (Вторая теорема Абеля ) Если ряд (1) имеет радиус сходимости R, то он сходится равномерно в любом замкнутом круге радиуса r < R.
∞
Доказательство: По первой теореме Абеля ряд ∑ ck r k сходится, кроме того
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k =0 |
|
|
|
|
|
|
|
r k |
z |
k |
|
|
|
|
|
|
|
c |
|
zk |
|
= |
c |
|
≤ |
|
c r k |
|
для всех z: |z| ≤ r. По признаку Вейерштрасса ряд сходится равномерно на |
|||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|||||||||||
|
|
k |
|
|
|
|
k |
r |
|
|
k |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
этом множестве.
9

Логинов А.С. Лекции по ТФКП
|
|
Теорема (Коши, Адамар) Радиус сходимости ряда |
(1) определяется по формуле R= |
|
|
1 |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
limn | c |
| |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n →∞ |
n |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ = |
|
,0 |
= |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Согласно следствию 2 из первой теоремы Абеля, радиус сходимости комплексного |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|||
степенного ряда совпадает с радиусом сходимости вещественного степенного ряда ∑| ck | xk |
, |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k =0 |
|
|
|
|
|
|
|||||
радиус сходимости которого определяется по формуле |
|
|
1 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
limn | c | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n →∞ |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Примеры: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
∑2k z k 2 |
, имеем cn = 0, если n ≠ k2, cn = 2k, если n = k2. Поэтому |
lim |
n | cn |
| |
|
= lim k 2 |
| c |
2 |
| , |
|||||||||||||||||||||||||||||||
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n →∞ |
|
|
|
k →∞ |
|
|
k |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
так остальные коэффициенты при n ≠ 0,cn=0. Далее lim k 2 |
|
|
|
|
|
|
= lim k 2 |
| 2k | = lim k |
|
|
= 1 . |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
| c |
2 |
| |
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k →∞ |
|
|
k |
|
|
|
|
k →∞ |
|
|
|
k →∞ |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2) Функция ez , z C . По определению полагаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
∞ |
|
z |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
ez = ∑ |
|
|
, по признаку Даламбера R = ∞, либо согласно следствию 2 из первой теоремы |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
k = 0 k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Абеля . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3) Функция sin z , z C . По определению полагаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
∞ |
|
|
|
z |
2k +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
sin z = ∑(−1)k |
|
|
, рассматривая соответствующий вещественный ряд и используя |
|
|
|||||||||||||||||||||||||||||||||||
|
|
(2k + |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
k =0 |
|
1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
следствие 2 из первой теоремы Абеля, получим R = ∞. Из определения следует, что sin (-z) = - sin z. 4) Функция cos z , z C . По определению полагаем
∞ |
z |
2k |
|
||
cos z = ∑(−1)k |
|
|
, рассматривая соответствующий вещественный ряд и используя |
||
(2k )! |
|||||
k = 0 |
|
||||
следствие 2 из первой теоремы Абеля, получим R = ∞. Из определения следует, что cos (-z) = cos z. 5) Функция sh z , z C . По определению полагаем
|
|
|
|
|
∞ |
|
|
|
z |
2 k +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
sh z = ∑ |
|
|
|
|
|
|
|
|
|
, рассматривая соответствующий вещественный ряд и используя следствие |
||||||||||||||||||||||||||||
(2k + 1)! |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 из первой теоремы Абеля, получим R = ∞. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
6) Функция ch z , z C . По определению полагаем |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
∞ |
|
|
z |
2k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ch z = ∑ |
|
|
|
|
|
, рассматривая соответствующий вещественный ряд и используя следствие 2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
k =0 |
|
(2k )! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
из первой теоремы Абеля, получим R = ∞. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
2.Свойства экспоненциальной и основных тригонометрических функций. |
||||||||||||||||||||||||||||||||||||||
a) |
|
eiz |
= cos z + i sin z , действительно |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
∞ |
n |
|
n |
∞ |
|
|
|
2k |
|
2 k |
|
∞ |
2k +1 |
|
|
2k +1 |
∞ |
(−1) |
k |
|
2k |
∞ |
(−1) |
k |
|
2k +1 |
||||||||||||
eiz = ∑ |
i |
|
z |
|
= ∑ |
i |
|
|
|
z |
|
|
+ ∑ |
i |
|
z |
|
|
= ∑ |
|
z |
|
+ i∑ |
|
z |
|
= cos z + i sin z . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2k + |
|
||||||||||||||||
n=0 |
k! |
k =0 |
|
2k! |
k =0 (2k +1)! |
k =0 |
2k! |
|
k =0 |
1)! |
|
|||||||||||||||||||||||||||
Следствие: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
eiz |
+ e−iz |
|
|
|
|
|
eiz − e |
−iz |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
c) cos z = |
|
|
|
|
|
|
|
|
|
|
|
, sin z = |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2i |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример: |sin (iy) | = |
|
e− y |
− e y |
|
=|sh y|→ ∞ при y→ ∞. Синус (и косинус) по модулю может быть |
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
2i |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
больше единицы в комплексной области.
10
