
- •Основные понятия теории вероятности. Эксперимент и его пространство элементарных событий.
- •Классификация событий. Действия над событиями.
- •3) Классическое определение вероятности, геометрическое определение вероятности, статистическое определение вероятности.
- •4) Элементы комбинаторики (принцип перестановки, размещения, сочетания).
- •5) Теорема сложения вероятностей.
- •6) Зависимые и независимые события. Умножение вероятностей.
- •7) Формула полной вероятности.
- •8) Формула Байеса:
- •9) Последовательность независимых испытаний. Формула Бернулли.
- •10) Предельный переход для фб (локальная и интегральная теоремы Лапласа).
- •11) Теорема Пуассона. Простейший поток событий.
- •12) Случайные величины. Закон распределения случайной величины.
- •13) Дискретные случайные величины и их законы распределения.
- •14) Числовые характеристики дискретных случайных величин.
- •15) Непрерывные случайные величины и их законы распределения.
- •17) Свойства дисперсий.
- •18) Биномиальное распределение.
18) Биномиальное распределение.
Биномиальное
распределение
(закон
распределения Бернулли)
описывает повторяющиеся независимые
опыты. Этот закон определяет появление
события
![]() раз при
раз при
![]() независимых испытаниях, если вероятность
появления события в каждом из этих
опытов
независимых испытаниях, если вероятность
появления события в каждом из этих
опытов
![]() не изменяется от опыта к опыту. Вероятность:
не изменяется от опыта к опыту. Вероятность:
![]() ,
,
где: – известная вероятность появления события в опыте, не изменяющаяся от опыта к опыту;
![]() – вероятность
не появления события в опыте;
– вероятность
не появления события в опыте;
![]() – заданное
число появления события в
опытах;
– заданное
число появления события в
опытах;
 – число
сочетаний из
элементов по
.
– число
сочетаний из
элементов по
.
19) Распределение Пуассона.
С
лучайная
величина X
называется
распределенной
по закону Пуассона
с параметром
![]() ,
если
эта случайная величина может принимать
значения
,
если
эта случайная величина может принимать
значения
![]() ,
соответствующая
вероятность которых определяется по
формуле Пуассона, когда
,
соответствующая
вероятность которых определяется по
формуле Пуассона, когда
![]() :
:
20) Геометрическое распределение.
Случайная величина X , которая принимает значение k (k =1,2,...) с вероятностью
 =
p
=
p

называется распределенной по геометрическому закону с параметром p .
21) Равномерное распределение.
Нормальный
закон распределения
(закон
Гаусса) полностью
определяется двумя параметрами –
математическим ожиданием
![]() и среднеквадратическим отклонением
и среднеквадратическим отклонением
![]() .
.
Аналитическое выражение нормального закона имеет вид:

22) Нормальное распределение.
Нормальным
называется такое распределение случайной
величины
![]() ,
плотность вероятности которого
описывается функцией Гаусса:
,
плотность вероятности которого
описывается функцией Гаусса:
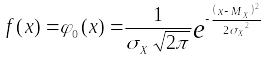
23)
24) Система случайных величин. Функция распределения двумерных случайных величин и её свойства.
Совокупность n случайных величин (X1,X2,...,Xn), рассматриваемых совместно, называется системой n случайных величин.
Ф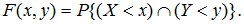 ункция
распределения двумерных случайных
величин:
ункция
распределения двумерных случайных
величин:
Свойства функции распределения двумерных случайных величин:
Функция распределения принимает значения из промежутка
 :
:
 .
.Вероятность того, что случайная величина примет значение из полуинтервала
 ,
равна разности
,
равна разности
 :
:
 .
.Функция распределения – неубывающая функция, т.е.
 при
при
 .
.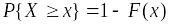 .
.Если
 ,
то
,
то
 .
.Если
 ,
то
,
то
 .
.
25) Плотность распределения непрерывных случайных двумерных величин и их свойства.
26)
27) Условные законы распределения.
28)
29) Числовые характеристики двумерных случайных величин.
1) Математическое ожидание. Пусть (x , h) - двумерная случайная величина, тогда M(x , h )=(M(x ), M(h )), т.е. математическое ожидание
2) Дисперсия. Если (x , h ) - двумерная случайная величина, то Dx = M(x - Mx )2 = Mx 2 - M(x )2, Dh = M(h - Mh )2 = Mh 2 - M(h )2.
30) Корреляционный момент. Коэффициент корреляции.
Х![]() арактеристикой
зависимости между случайными величинами
X
и Y
служит математическое ожидание
произведения отклонений X
и Y
от их центров распределений, которое
называется корреляционным
моментом
или ковариацией:
арактеристикой
зависимости между случайными величинами
X
и Y
служит математическое ожидание
произведения отклонений X
и Y
от их центров распределений, которое
называется корреляционным
моментом
или ковариацией:
К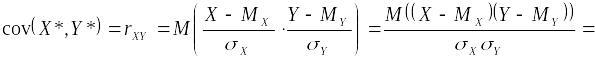
 овариация
овариация
![]() и
и
![]() называется коэффициентом
корреляции
случайных величин
и
называется коэффициентом
корреляции
случайных величин
и
![]() (обозначается
(обозначается
![]() ).
).
![]()
