10) Предельный переход для фб (локальная и интегральная теоремы Лапласа).
Локальная теорема Лапласа. Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то вероятность Pn (k) того, что событие A произойдет k раз в n независимых испытаниях, удовлетворяет предельному равенству:
Интегральная теорема Лапласа. Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то вероятность Pn (k1,k2) того, что событие A произойдет не менее k1 и не более k2 раз в n независимых испытаниях, удовлетворяет предельному равенству:
11) Теорема Пуассона. Простейший поток событий.
Т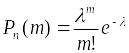
еорема
Пуассона.
Если
вероятность p
наступления события A
в каждом испытании постоянна и мала, а
число независимых испытаний n
достаточно велико, то вероятность того,
что событие A
наступит
m
раз,
приближенно равна:
где
.
Простейшим (пуассоновским) называют поток событий, который обладает свойствами стационарности, ординарности и отсутствия последействия.
Свойство стационарности означает, что вероятность появления k событий в любом промежутке времени зависит только от длительности t промежутка времени и не зависит от начала его отсчета.
Свойство ординарности означает, что появление двух или более событий за малый промежуток времени практически невозможно, т.е. события появляются не группами, а поодиночке.
Свойство отсутствия последействия означает, что вероятность появления k событий в любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка.
12) Случайные величины. Закон распределения случайной величины.
Случайной величиной называется функция X = X (ω), определенная на множестве элементарных событий Ω, ω ϵ Ω.
Случайная величина, принимающая конечное или счетное множество значений, называется дискретной (ДСВ).
Если же множество возможных значений случайной величины несчетно (заполняет некоторый интервал), то такая величина называется непрерывной (НСВ).
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения может иметь разные формы.
13) Дискретные случайные величины и их законы распределения.
Случайная величина, принимающая конечное или счетное множество значений, называется дискретной (ДСВ).
Дискретная случайная величина принимает конечное число возможных значений xi (где i = 1… n или i = 1 … ∞) с определенными вероятностями.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и вероятностями их появления.
Дискретная случайная величина считается заданной, если известен ее закон распределения, который может иметь разные формы:
Рядом распределения ДСВ X называется таблица, в которой перечислены возможные значения x1, x2, …, xn случайной величины и соответствующие им вероятности p1, p2, …, pn .
Графическое изображение ряда распределения называется многоугольником распределения.
Функцией распределения случайной величины X называется функция F(x), задающая вероятность того, что случайная величина X принимает значение, меньшее x , т.е.:
F(x) = P(X < x) .