
- •Оглавление
- •Введение
- •1. Матрицы рассеяния элементов цепей свч
- •2. Мостовые устройства свч
- •2.1. Синфазный делитель мощности (мост Уилкинсона)
- •2.2. Квадратурный (шлейфный) мост
- •2.3. Синфазно-противофазный (кольцевой) мост
- •3. Линии передачи, используемые в устройствах свч
- •3.1. Симметричная полосковая лп
- •3.2. Несимметричная полосковая линия (микрополосковая)
- •3.3 Копланарная линия (копланарный волновод)
- •3.5. Связанные линии передачи
- •4. Направленный ответвитель на основе связанных лп
- •5. Мостовые устройства на основе сосредоточенных реактивных элементов
- •6. Резонаторы свч
- •6. 1. Поле коаксиального резонатора
- •6.2. Поле прямоугольного резонатора
- •6.3. Возбуждение резонаторов
- •6. 4. Эквивалентные параметры отрезков лп, используемых в качестве резонаторов
- •7. Фильтры свч
- •8. Линейные усилители свч
- •9. Параметрические устройства свч
- •9.1. Теоретические сведения
- •9.1.1. Идеальный ключевой преобразователь частоты
- •9.1.2. Диодные преобразователи частоты
- •9.2. Диодные свч-преобразователи частоты
- •9.3. Коммутаторы на основе pin диодов
- •9. 4. Применение диодных ключей
- •10. Аттенюаторы свч
- •11. Об использовании коаксиальных линий для свч устройств различных частотных диапазонов
- •12. Невзаимные устройства свч
- •12. 1 Свободные колебания вектора намагниченности электрона
- •12. 2. Вынужденные колебания вектора намагниченности электрона, тензор магнитной проницаемости ферромагнетика.
- •12. 3. Распространение плоской электромагнитной волны в неограниченной ферритовой среде, намагниченной вдоль направления движения волны
- •12. 4. Ферритовые устройства на основе круглого волновода
- •12.5. Ферритовые устройства на основе прямоугольного волновода
- •12. 6. Ферритовые устройства на основе линий передачи с т-волнами
- •12. 7. Ферритовые резонаторы
- •13. Свч автогенераторы
- •13.1 Теоретические сведения
- •13.1.1 Линейная теория автогенератора
- •13.1.2. Об использовании отрезков линий передачи
- •13. 1. 3. О фазовых шумах аг
- •13. 2. Конструкции автогенераторов свч
- •13. 3. Мощные аг свч
- •14. Усилители мощности свч
- •14.1. Простейшие согласующие цепи
- •14. 1. Расчет стационарного режима автогенератора
- •15. Пассивные нелинейные устройства свч
- •16. О программных средствах для компьютерного моделирования устройств свч
- •Список литературы
14.1. Простейшие согласующие цепи
Рис. 14. 1
 Д
Д![]() цепей
можно использовать резонансные цепи в
цепей
можно использовать резонансные цепи в
разных комбинациях. Рассмотрим некоторые из них.
В схеме 14. 1 согласуемая цепь есть последовательной соединение . Формулы для расчета элементов цепи приведены ниже:
 .
Так как постоянная
не
может быть отрицательна, нагруженная
добротность цепи должна удовлетворять
условию
.
Так как постоянная
не
может быть отрицательна, нагруженная
добротность цепи должна удовлетворять
условию
 .
Очевидно, что это условие может быть
выполнено только, если
.
Очевидно, что это условие может быть
выполнено только, если
![]() .
Значение
.
Значение
![]() определяет
полосу частот согласования:
определяет
полосу частот согласования:
 (
(![]() центральная
частота полосы согласования). Для
параллельного включения
и
центральная
частота полосы согласования). Для
параллельного включения
и
![]() можно использовать согласующие цепи
рис. 14. 2 и 14. 3.
можно использовать согласующие цепи
рис. 14. 2 и 14. 3.
Рис. 14. 2
Рис. 14. 3


Для цепи рис. 14. 2:
 .
Условие реализуемости:
.
Условие реализуемости:

Для цепи рис. 14. 3:
 .
Условия реализуемости:
.
Если по какой либо причине желательно,
чтобы согласующая цепь имела индуктивный
вход, то можно воспользоваться цепью
рис.14. 4. Если согласуется параллельная
цепь, то ее надо пересчитать в
последовательную.
.
Условия реализуемости:
.
Если по какой либо причине желательно,
чтобы согласующая цепь имела индуктивный
вход, то можно воспользоваться цепью
рис.14. 4. Если согласуется параллельная
цепь, то ее надо пересчитать в
последовательную.
Рис. 14. 4

 .
Условие реализации:
.
Условие реализации:
 .
Так
как расчетные формулы для согласующих
цепей даны без вывода, необходимо сказать
несколько слов об алгоритме их вывода.
Исходными данными является частота, на
которой достигается согласование, и
полоса частот, в которой рассогласование
не превосходит заданные пределы. Полоса
определяет нагруженную добротность
.
Так
как расчетные формулы для согласующих
цепей даны без вывода, необходимо сказать
несколько слов об алгоритме их вывода.
Исходными данными является частота, на
которой достигается согласование, и
полоса частот, в которой рассогласование
не превосходит заданные пределы. Полоса
определяет нагруженную добротность
 .
Здесь
полоса
частот,
частота,
на которой достигается полное согласование.
Значения R1
и Сout
предполагаются известными. Рассматривая
рис. 14. 1, 14. 2, 14. 3, 14. 4, очевидно, что
неизвестными являются три реактивности.
Следовательно, для их определения
необходимо иметь три уравнения. Эти
уравнения получаются из общего уравнения
для входного сопротивления согласующей
цепи (вместе с согласуемой цепью) со
стороны сопротивления RL,
при наложении следующих условий: входное
сопротивление должно быть чисто активным
и равным RL
и добротность цепи имеет заданное
значение
.
Приравнивая мнимую часть сопротивления
нулю (она состоит из емкостной и
индуктивной частей), мы получаем
возможность задать характеристическое
сопротивление цепи
.
Здесь
полоса
частот,
частота,
на которой достигается полное согласование.
Значения R1
и Сout
предполагаются известными. Рассматривая
рис. 14. 1, 14. 2, 14. 3, 14. 4, очевидно, что
неизвестными являются три реактивности.
Следовательно, для их определения
необходимо иметь три уравнения. Эти
уравнения получаются из общего уравнения
для входного сопротивления согласующей
цепи (вместе с согласуемой цепью) со
стороны сопротивления RL,
при наложении следующих условий: входное
сопротивление должно быть чисто активным
и равным RL
и добротность цепи имеет заданное
значение
.
Приравнивая мнимую часть сопротивления
нулю (она состоит из емкостной и
индуктивной частей), мы получаем
возможность задать характеристическое
сопротивление цепи
![]() на
частоте согласования, значение которого
определяется добротностью:
на
частоте согласования, значение которого
определяется добротностью:
![]() .
Пусть входное сопротивление равно
.
Пусть входное сопротивление равно![]() ,
где
,
где
 .
Первое слагаемое соответствует
положительной части входной реактивности,
второе отрицательной. На частоте
.
Первое слагаемое соответствует
положительной части входной реактивности,
второе отрицательной. На частоте
![]() они должны быть равны. Очевидно, что
они должны быть равны. Очевидно, что
![]() и должны выполняться условия
и должны выполняться условия
![]() и
и
 .
Таким образом получаем три уравнения
из которых определяются сопротивления
всех трех реактивностей согласующей
цепи.
.
Таким образом получаем три уравнения
из которых определяются сопротивления
всех трех реактивностей согласующей
цепи.
14. 1. Расчет стационарного режима автогенератора
Крутизна
характеристики АЭ по первой гармонике
 ,
где
,
где
 ,
,
![]() амплитуда
напряжения на входе АГ (между базой
(затвором) и эмиттером (истоком)),
амплитуда
напряжения на входе АГ (между базой
(затвором) и эмиттером (истоком)),
![]() ,
,
![]() крутизна
спрямленной входной характеристики
АЭ. Тогда
крутизна
спрямленной входной характеристики
АЭ. Тогда
![]() .
Из условия «баланса амплитуд»
.
Из условия «баланса амплитуд»
![]() значение
определится как
значение
определится как
 .
Выбрав значение угла отсечки
,
от которого зависит КПД АГ, перейдем к
определению сопротивления нагрузки
,
рассчитав АГ в стационарном режиме как
усилитель с отсечкой выходного тока.
Мощность колебаний первой гармоники
определится как
.
Выбрав значение угла отсечки
,
от которого зависит КПД АГ, перейдем к
определению сопротивления нагрузки
,
рассчитав АГ в стационарном режиме как
усилитель с отсечкой выходного тока.
Мощность колебаний первой гармоники
определится как
 .
Здесь
амплитуда
тока первой гармоники, зависящая от
угла отсечки,
.
Здесь
амплитуда
тока первой гармоники, зависящая от
угла отсечки,
![]() амплитуда
напряжения первой гармоники на
сопротивлении
,
близкая к напряжению питания АГ.
амплитуда
напряжения первой гармоники на
сопротивлении
,
близкая к напряжению питания АГ.
![]() ,
,
![]() .
Тогда
.
Тогда
 .
Параллельное (по отношению к КК АГ)
сопротивление
.
Параллельное (по отношению к КК АГ)
сопротивление
 ,
где
,
где .
Здесь
.
Здесь
 ,
,
 .
.
![]() емкость,
включенная между базой (затвором) и
эмиттером (истоком),
емкость,
включенная между базой (затвором) и
эмиттером (истоком),
![]() емкость,
включенная между коллектором (стоком)
и общим проводом.
емкость,
включенная между коллектором (стоком)
и общим проводом.
![]() входное
сопротивление устройства, которому АГ
отдает мощность. От значения сопротивления
зависит
нагруженная добротность КК АГ. Обычно
выбирают
входное
сопротивление устройства, которому АГ
отдает мощность. От значения сопротивления
зависит
нагруженная добротность КК АГ. Обычно
выбирают
![]() и сопротивление потерь контура
и сопротивление потерь контура
![]() .
Отсюда следует соотношение
.
Отсюда следует соотношение
 и
и
 .
Для фазосдвигающей цепочки (последовательно
включенных
и
)
можно получить соотношение
.
Для фазосдвигающей цепочки (последовательно
включенных
и
)
можно получить соотношение
 ,
откуда
,
откуда
 .
Значение
.
Значение
 .
Для выбора угла отсечки определим КПД
АГ:
.
Для выбора угла отсечки определим КПД
АГ:
 .
График функции
.
График функции
 приведен на рис.14. 1. При выборе
и
приведен на рис.14. 1. При выборе
и
![]()
![]() ,
при уменьшении угла отсечки КПД
возрастает, при увеличении – падает.
,
при уменьшении угла отсечки КПД
возрастает, при увеличении – падает.
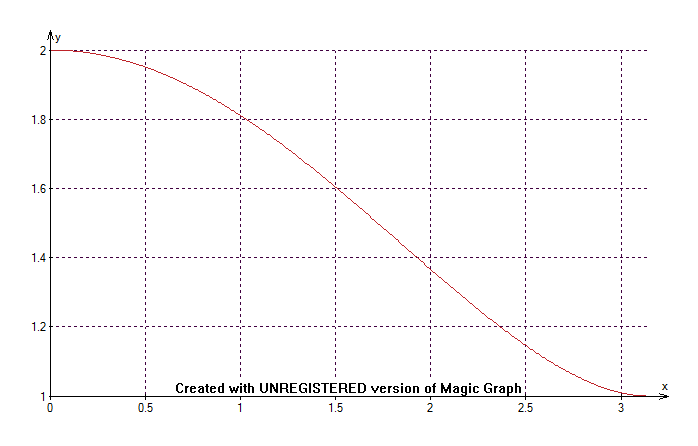
Рис. 14. 1
