13.1.2. Об использовании отрезков линий передачи

в качестве индуктивностей в ГУН.

Отрезок ЛП, закороченной на конце, длиною менее имеет входное сопротивление вида , где волновое сопротивление ЛП; ( параметры среды, заполняющей ЛП, длина волны в ЛП); геометрическая длина ЛП. Если не учитывать потери в ЛП, то является чисто мнимым и имеет индуктивный характер. При тангенс обращается в бесконечность. Следовательно, можно использовать равенство , где эквивалентная индуктивность ЛП. Тогда . В отличие от обычной сосредоточенной индуктивности зависит от частоты. Если угол меньше 30°, то тангенс можно заменить его аргументом. Тогда и для коротких отрезков ЛП можно считать, что не зависит от частоты. Однако для получения больших значений приходится увеличивать , что приводит к росту потерь и снижению добротности. При использовании отрезков ЛП с углом , большим 45˚, величина становится существенно зависимой от частоты, так как с ростом частоты функция растет быстрее, чем частота, и, следовательно, значение растет с увеличением частоты. Для АГ, работающих на фиксированной частоте, это не имеет значения, однако является существенным для ГУН. Действительно, если выбрать на нижней частоте, при максимальной емкости варикапа, то при уменьшении емкости варикапа и росте частоты, генерируемой ГУН, в свою очередь будет расти , что приведет к уменьшению частоты по сравнению с ГУН, в котором используется сосредоточенная индуктивность. Таким образом перекрытие по частоте для ГУН с отрезком ЛП (резонатором, чаще всего коаксиальным) меньше, чем для ГУН с сосредоточенной индуктивностью. Оценим приближенно изменения частоты в ГУН с сосредоточенной индуктивностью и в ГУН с резонатором. В ГУН СВЧ полная емкость КК АГ зависит от управляющего напряжения , т. е. . Резонансная частота КК с сосредоточенной индуктивностью определится как , где индуктивность КК. Преобразуем это выражение так, чтобы в него входило сопротивление индуктивности , тогда получим: , или . Следовательно, для ГУН с коаксиальным резонатором (КР) . Оценим теперь изменение резонансной частоты для обоих КК при изменении емкости . Очевидно, что для КК справедливо отношение 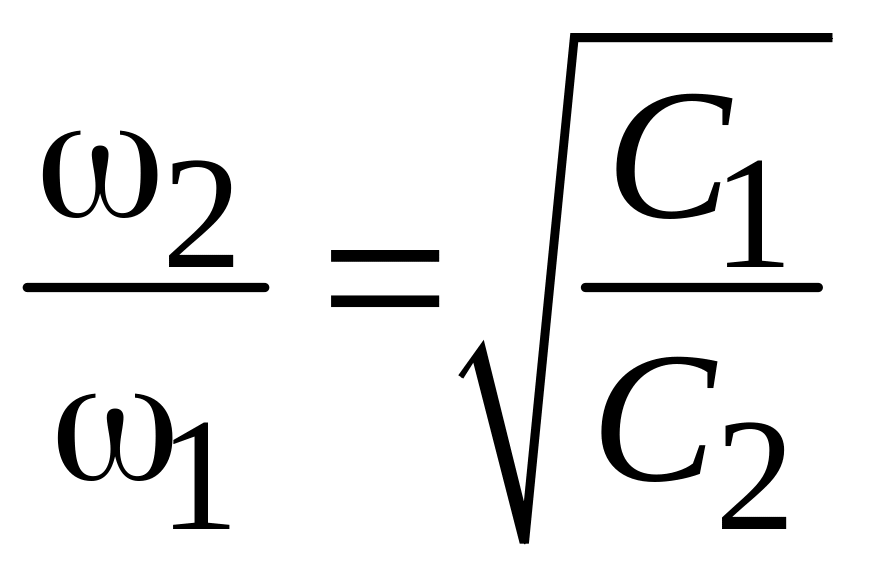. Для резонаторного КК функция зависит от частоты и для резонансных частот будут справедливы уравнения вида: . Поделив одно на другое, получаем равенство , в котором неизвестным является только длина КР . Для определения длины получаем трансцендентное уравнение , решить которое проще всего графически в любой математической программе. По найденному находится из выражения . В данном случае эквивалентная индуктивность КК представляет собой последовательное соединение емкости варикапа и сосредоточенной индуктивности L. Заменяя индуктивность резонатором, получаем на частоте уравнение: , где ‒ емкость варикапа, обеспечивающая выполнение равенства. Такое же уравнение можно записать для частоты : . Из этих уравнений получаем трансцендентное уравнение для определения длины КР : 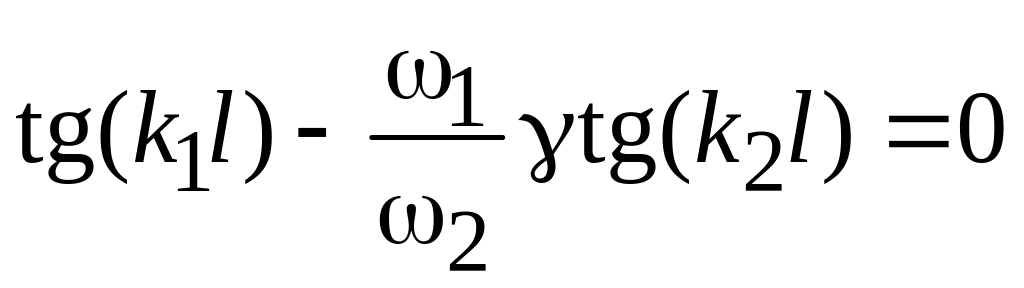, где . Решая уравнение графическим путем, находим длину . Волновое сопротивление находим из уравнения . Перейдем теперь к вопросу о фазовых шумах. Фазовые шумы (ФШ) являются одним из важнейших параметров АГ. Эти шумы образуются вследствие преобразования шумовых напряжений, создаваемых активным элементом АГ и активными сопротивлениями его схемы, в фазомодулированные колебания. Преобразование происходит на реактивных элементах, зависящих от напряжения (варикапы, емкости транзисторов и диодов). Наибольшими ФШ обладают ГУН с управляющим элементом в виде варикапа. Уровень фазовых шумов зависит от производной , где управляющее напряжение на варикапе. Найдем значение этой производной для ГУН с сосредоточенной индуктивностью :

.

Для ГУН с КР: .

Сравнивая оба эти выражения, приходим к выводу, что для ГУН с КР абсолютное значение производной в 2 раза больше, чем для ГУН с сосредоточенной индуктивностью. Это значит, что при прочих равных условиях уровень фазовых шумов для ГУН с КР на 6 дБн выше, чем для ГУН с сосредоточенной индуктивностью (дБн ‒ уровень по отношению к уровню несущей частоты).

Интервал изменения частоты в ГУН с отрезком ЛП в качестве индуктивности будет всегда меньше, нежели для ГУН с сосредоточенной индуктивностью. Чем больший угол выбран на нижней частоте, тем меньше достижимое изменение частоты при той же вариации емкости варикапа.