14. Распределение силы между витками резьбы в резьбовых соединениях.

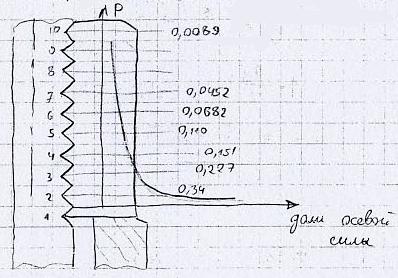
Задача о распределении нагрузки между витками резьбы является статически неопределимой и для ее решения рассматривают условие совместности деформаций тела винта и гайки.

Эта задача решена Жуковским в 1902 году в предположении что погрешность по шагу винтов резьбы равна 0.

Из рисунка видно, что первый виток со стороны опорной поверхности воспринимает 34% всей нагрузки => в крепежном соединении нет смысла применять слишком высокие гайки. По ГОСТ Н_гайки ~ 0,8d

15. Расчет резьбы на срез и смятие

При одинаковой прочности винта и гайки, расчет ведут по винту.

Для резьбы винта:

τ₁ = , где

Н_гайки – высота гайки

К = р` / p – коэффициент полноты резьбы (для метрической 0,87)

К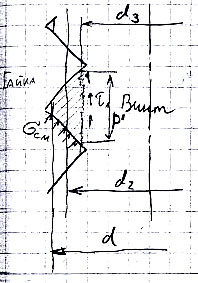 _м – коэффициент, учитывающий неравномерность распределения нагрузки по виткам резьбы

К_м = 0,7…0,75

[τ]_ср1 = (0,2…0,3)  σ_Т

σ_cм =  [σ]_см , где

Z = H_Г / P – число витков

При выполнении условия равнопрочности стержня и гайки достаточной оказывается высота гайки H_Г = 0,65d , а по ГОСТ H_Г = 0,8d , что подтверждает нецелесообразность расчетов резьбы на прочность.

16. Расчёт резьбового соединения при действии силы затяжки.

На винт действует осевая сила F_зат и момент в резьбе Т_р. Этот случай для всех затянутых соединений. В стержнях возникает нормальное напряжение σ_р от силы Fзат и касательных нагрузок τ_р от Т_р .

В этом случае расчет ведется по эквивалентным напряжениям

σЕ =

σ_р = 4 F_зат / (π  d₃²)

τ = T_p / W_p =

σ_Е = σ_р

Геометрическое подобие резьб позволяет принять

d₂ / d₃ ≈ 1,1

ψ = 2,5 град

f₁ = 0,15

γ₁ = 8,5 град

σ_Е = σ_р  1,3

Условие прочности винта можно записать в виде

σ_Е = 1,3  4 F_зат / (π  d₃²)  [σ]_р

Иными словами, действие момента Т_р учитывается увеличением напряжений от F_зат в 1,3 раза.

При проектном расчете определяют

d₃  => из ГОСТ определяют резьбу

17. Расчет групп резьбовых соединений при действии нагрузки в плоскости стыка

Под групповыми соединениями понимают такие соединения в которых число болтов > 2.

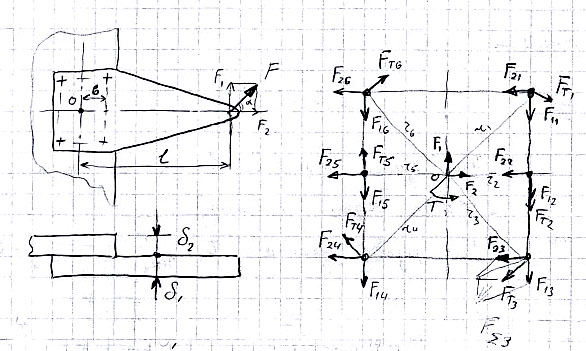
Встречаются два типа таких соединений:

1. нагрузка действует в плоскости стыка соединяемых деталей

2. нагрузка действует в плоскости перпендикулярной стыку

В расчетах принимают допущения:

• Деформации соединяемых деталей не учитываются (жетали абс. жесткие)

• Возможный взаимный поворот соединяемых деталей от момента происходит относительно центра тяжести сечений винтов (т. О)

• Внешние нагрузки передаются с одной детали на другую локально через зоны, расположенные вокруг винтов

• Силы F_Ti в винтах прямо проп-ны расстоянию до них от т. О, т.е.

F_T1 / r₁ = F_T2 / r₂ = ... = F_Ti / r_i (1)

Условия равновесия для соединения могут быть записаны в виде системы:

Z₁  F_T1 r₁ + ... + Z_i  F_Ti  r_i = T

F₁₁ + F₁₂ + ... + F_1i = F₁ (2)

F₂₁ + F₂₂ + ... + F_2i = F₂

Z_i – число болтов, находящихся на одинаковом расстоянии от т. О

Выразив силы F_T2...F_Ti через F_T1 с учетом (1), получим

F_T1  (Z₁ r₁² + … + Z_i  r_i²) = T  r₁

Отсюда сила от момента на наиболее нагруженные винты, расположенные на расстоянии r₁ от точки О, равна

F_T1 = F_T2 = F_T4 = F_T6 = T  r₁ / (Z₁  r₁² + … + Z_i  r_i²) = T  r₁ / (Z_i  r_i²)

Cоставляющие силы F, приведенные к т. О, распределены по винтам равномерно и равны:

F₁₁ = F₁₂ = ... = F_1i = F₁ / Z

F₂₁ = F₂₂ = ... = F_2i = F₂ / Z

Проведя геометрическое суммирование векторов на каждом винте, определяем

F_MAX = F_T3 + F₁₃ + F₂₃ = F_3

Для определения диаметра винта рассчитывают одиночное болтовое соединение, нагруженное силой F_MAX