42. Фазовое пр-во з-н сохран потока точек фаз про-ва.
Фаз пр-во-совок точ,положкоторопредобобщ корд и обощимп мех сист.Размер фаз пр-ва опред числом обощкоорд и имп.
Теорема о непрерывнпл-ти точекфазового пространст- совок точ ФП – сов точ этого пр-ва в опред мом врем.При дв мех сис распре точ ФП меняет.
Введём пл-ть потока точекФП:
или
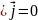– ЗС пл-ти потока точек ФП
Док-во:
ур-я
движ в канонич форме:
и
то
43.ТеоремаЛиувиля.
Если для мех.сист с R степенями свобод коорд фаз точудовл канон ур-ю движ, то объём фазов точек мех сист не мен со врем.
Док-во:рассмотр
объёмы: V0=
и
в момент врем
V1=
переход
от объема в мом врем
осущ с помощью ЯкобианаD:
V1=
D=
Можем видеть что з-н преобр объёма отражат з-н преобр якобиана- найдём его в произ мом врем.
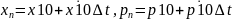
Якобиан=
Ограничперв
порядком малости по перввелич
и раск якобD=1+
=>
44. Канонические преобразования.
,
Основ суть –упрощрешур-й. Должны быть согласов с принципом наименьш действ.
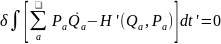учтём
гу(
)
=0
–произв ф-я
и
т.к пределыинтвыбпроизв образом, под
функ должна =0 то в новых кононкоорд
45. Ур-еГамельтона-якоби.
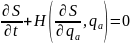
Част проbзводная по врем от ф-ии действ.
Вычпр-ю
слева: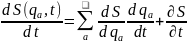
диффур-ние в частнпроизвх 1-го порядка, описдвиж голономных механич. систем под действ потенц. сил.
Чтобы сост ф Г.- Я. для данной механич. системы надо знатьфункцию Гамельтона H(qi, pi, t), гдеqiирi- - канонич. переменные: обобщённые координаты и обобщённые импульсы, at- время.
46. Движзар частиц в эл-магн поле в формалЛагран.
2-й
з-н Ньютон
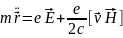
Состав
ф-ю Лагранжа:
-ур-е
Лагр-Эйлер
Обощкоордx,y,z.
,
,
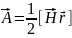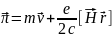E=-
47. Движзар частиц в эл-магн поле в формалГамель.
,E=-
-
=
– полнэнерг.
-ур-е Лагр-Эйлер
48.Определкинетич энергии вращтв. Тела.
Абсолют тв тело, у которого нет растяж и сжат
Число степ своб у свобвращ тела =6.
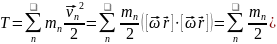
49.Момент импульса вращтв. Тела.
Абсолют тв тело, у которого нет растяж и сжат
Число степ своб у свобвращ тела =6.
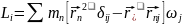
Теоремаоб
измен момента ипм:
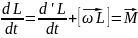
50. Определполнпроизв по врем от вектор физвелич с учёт вращ системы.
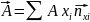-3х мерный вектор
Ориентац нормали бут мен со врем
;
=>
– 1-е слаг – обычпр-я
2-е слагсвяз с вращсист.
51. Ур-еэйлера для вращтв тела.
Берём производную в неинерцСО
пишем её для мом импL
– спроект на оси
3-и ур-я
Определим
Получур-я эйл в компон:
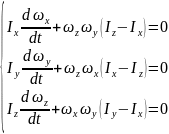
58. Кинематич перемен в релятив механике.
4-х мерные импульс, масса, скорость.
Универсалькинематич соотношение:
скорость :
52. РешУр-еэйлера для нутационвращтв тела.
Запишемр-е Эйлер для вращдв тела по компонентам:
т.к бум расматр
то
и
рассматр два уравнениявведём
продифпо
врем 1-е ур-е и преобраз 2-е:
–его решением явл
тогда
если нач фаза =0Следствия
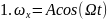3.
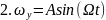
53.ФизинтерпретацРеш Ур-е эйлера для вращтв тела.
-описыв
в пл-тиxyокружность.
,
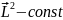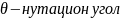
Таким образ вектора
остаются в 1-й пл-ти
Прецес
вращение в геометр интерпрет – когда
вращтвтело то конус катит по поверх
конуса образующ которого явлвектр
54. Вращение тела в поле силы тяжести.
Запишем функц Лагранжа для тверд тела в потенц поле сил: L = T- U = ½ I1 (φ’2·sin2θ + θ’2) + ½ I3 (φ’·cosθ + ψ’)2 – mgLcosθ
Обобщкоордφ и ψявлцикличкоорд, значит им соответств сохраняющиеся во врем обобщ импульсы:
Pφ= I1 φ’·sin2θ+ ½ I3 (φ’·cosθ + ψ’)·cosθ = const
Pψ= I3 (φ’·cosθ + ψ’)= const
Запишзаконсохранэнерг
E = ½ I1 (φ’2·sin2θ + θ’2) + ½ I3 (φ’·cosθ + ψ’)2 + mgLcosθ