Основные понятия теор. Меха.
Материальн.т-тело,размер которможнпренебр по сравн с растдвиж этого тела относ др тел. СостМ.топред с helpкордин и скор в определенный момент t.
Систотсч- выбир из мн-ва тел движ друг отност друга. Система отсчета состоит из тела отсчета,сист. координ. и врем.Релятвчастиц– описывается в 4-х мернпрост-время. Не релятив – простр и время отделимы.Мех движ- измен сост. тел друг относ.друга. Мех действ-действ. в следст. котор. измен сост тела друг относит друга. Сила-векторная величина, которявл мерой механического действия.Инертность- способ тела сохран состояние покоя или равномерногопрямолиндвиж.Масса-мера инертности тела.
Принцип относит Галил.Преобр Галилея
Принцип относит Галилея – все физ з-ны(З-ны Ньютона) незавсят от выб ИСО т.е протек вовсех ИСО одинаково.
ПреобразовГалил:
,y
= y’,
z
= z’,
t
= t’,
,
запишвекторно
:
ускор не мен при перех из одной ИСО в
др. Эти преобразовсправедл только для
нерелятив скоростей. В случае релятив
скоростей пользуемся преобразов
Лоренца.
З-ны Ньютона.Метод решения задач в механике Ньютон.
1)если на тело не действ др тела, то тело покоится или равномернпрямолиндвиж.
2)ускорv.т прямопропорц силе действующ со стороны др. тел или полей и обратнопроп массе этого тела.a = F/m
3)если рассматр систему состоящ из двух м.т, то действ первой м.т на вторую равно противоде. 2-й м.т на 1-ю.
Методика.реш.задач:
выбрать скорость, установ обобщён координаты, если несколько М.тперейти в систему центра масс, записать для обобщённых кордин 2-й закон Ньютна в диф. форме, получить диф. ура-е, решить его, найти константы использначуслов, получить закон движения.
ТеоремаобизменP(имп)и l(момент имп)м.Т.
Tеорема
об измен P(имп):
измен
импМ.т в ед врем = силе.
Если сила, действ
на М.т=0, то
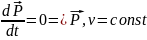
ТеоремаобизменL(момент
имп):
Измен момен имп М.т в ед. Врем= момент силы действ на эту М.т
Следствие:
Cвойства потенциальных полей.
Силов поле назпотенц
если
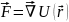=grad
Сил тяж,упруг, сила Кулона - пример потенцсилов поля.
Cвойства:
1)потенц поле отсут вихри
2)циркуляция по
любому замкн контуру =0
3)циркуляциянезавис от вида кривой.
т.к
-пол
диференцпотенци
определяется
заданием нач и конечнточ инезавис от
вида кривой.
4) векторные линии потенц поля не могут быть замкнут
5) сумма потенцильнвекторн полей естьпотенц поле, и потенциал суммы полей = сумме потенциалов.
Теоремаоб измен кинетичэнергМ.т.
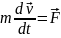т.к
=>
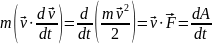Измен кинэнергМ.т в ед врем = работе соверш над М.т в ед времен=мощности.
Теоремаоб измен P(имп) мех.сист.
+
+
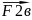
где внутренние силы (по 3 закНьют) сокращают.
– измен сум-го имп
мех. сист = сумвнеш сил,дейст на эту
сист.
Следств: 1) если
2) мех.систназзамкн, если действ внеш сил = 0
Выддвиж центра масс и относит движмехансист.
Введ нов СО(центра
масс):
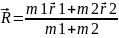радиус
вектор центра масс
– рад вект,характеризующ
относит движМ.тмех.сист
разр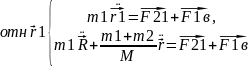
Относит
сложим скобки:
движ
мех сист как ед целое эквивалдвиж ЦМ
этой сист.
Если в кач СО выбсист ЦМ, то сумма импульсов=0
т.к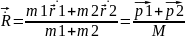
=>
и
R=0
путём перехода от произв СО к СО ЦМ количуравн уменьшается и решеннекотфиз задач упрощается.
Теоремаоб измен L момента импмехансист.
слева
векторно
на r1
и r2
+
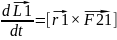Сложим эти ур-я
+
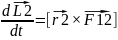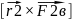
первыесоаг
лев части ур-й =0 только когда внут силы
мех систявл центральными, т.е действ
вдоль векторов соед 2-е М.т
Измен импмех.сист в ед. врем = действ суммы моментовсил, действ на каждМ.тсис.
Следств: если
систзамкнута, то мом импсохран:
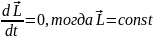
Теорема об измен кинет энерг Тмехансист.
умнож
скалярно на соотвv
Сложим ур-я
+(
)+
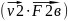
Изменение кинетич энергии мех сист в ед времени = сумме измен внеш и внутр работы за ед времени соверш над мех сист.
Описан Мат Маятн на осн 2-го з-н Ньют и ЗСЭ.
Есть пруж маятникподвеш горизонтально
Применим 2-й з-н Ньютона:
,
,
,
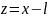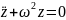Решив ур-е методом
Эйлера находим:
.
Получ такой же результ применив ЗСЭ
ЗСЭ
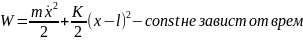
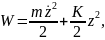выразим
производную: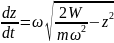
Разделим перемен
и проинтегр:
=>
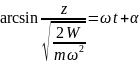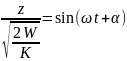
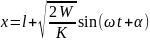
Описан упрколебМ.т на осн 2-го з-н Ньют и ЗСЭ.
Есть 2-е М.тсвяз пружиной. Теоремаоб измен кинэнерг:
и 3-й з-н Ньютона представл:
=
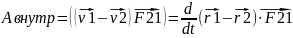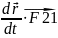т.к поле, действ на внутрМ.т потенциально,
можем запис:
=полндиффунцU=
по аналогии для
внешнего поля:
+
=
,
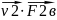где
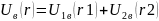
Получаем:
,
ЗСЭ:
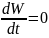тогда
,
где
1)т.к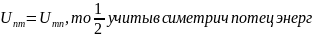
2)
-
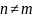исключаявзаимодМ.т с самой собой.
Связи.Ур-я связей.Типы перемещ.
Связь-совокуп тел ограничивающ движение зад тела.
Голономнаясвязь
-которописаналитическим
уравненf(
)=0
– общ ур-е связи. Неголономн – не опис.
Уравнен (св)мб несколько.Каждур-е
связиотнимает у М.тодну степ свободы.Если
связи нет, то у М.ттри степени свободы.
Если функцясвязи явно завис от врем –
нестацсв,
если явно не зав, то стацион.
Геометрсв-которобладгеом
формой. В случсистсост из NМ.т.
Число степ свободы S=3N-P,P
– колич св.
При движ вводят силы:
Активные силы-силы, которускордвМ.т или мех.сист. Пассивн силы-силы реакцсвязи.
3 вида перемещ:
- возможное – перемещ, кото подчинтолькоуравнсв.
-действительн-перемещм.т или мех. сис под дейстактивн и пассив сил.
-виртуальные -воображперемещ мат точ, подчинуравнен связи в фикс мом врем.