Задание 04 (тв Вероятность работы эл. Цепи)
48. Задание {{48}} ТЗ № 2
0.832
0.976
0.744
0.493
49. Задание {{49}} ТЗ № 7
0,8
0,6
0,92
0,48
50. Задание {{50}} ТЗ № 12
0.893
0.588
0.644
0.485
51. Задание {{51}} ТЗ № 17
0.742
0.821
0.426
0.844
52. Задание {{52}} ТЗ № 22
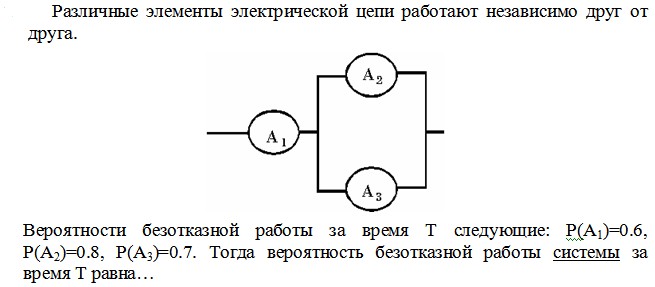
0,264
0,336
0,564
0,376
53. Задание {{53}} ТЗ № 10
В=А1+А2+А3+А4
В=А1·А4+А2+А3
В=А1+А2·А3+А4
В=А1·А2·А3·А4
Задание 05 (тв Условная вероятность. Полная вероятность. Формула Байеса и Бернулли)
54. Задание {{54}} ТЗ № 71
В цеху три типа автоматических станков производят одни и те же детали. Производительность их одинакова, но качество работы различно. Известно, что станки 1 -го типа производят 0,94 деталей отличного качества; 2-го - 0,9; 3-го - 0,85. Все изготовленные за смену детали сложены на складе в нерассортированном виде. Определить вероятность того, что взятая наудачу деталь окажется отличного качества, если станков 1-го типа - 5 штук, 2-го - 3 штуки, 3-го - 2 штуки.
0,91
0,89
0,87
0,84
55. Задание {{55}} тз № 72
В трех ящиках находятся однотипные изделия:
в 1-м - 10 изделий, из них 3 -нестандартных,
во 2-м - 15 иделий, из них 5 -нестандартных,
в 3-м - 20 изделий, из них 6 - нестандартных.
Наудачу выбирается 1 изделие и оно оказалось нестандартное.
Определить вероятность того, что взятое изделие принадлежало 2-му ящику.
5/14
2/11
3/8
5/7
56. Задание {{56}} тз № 73
Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность 1-го автомата вдвое больше производительности 2-го. Первый производит в среднем 60 % деталей отличного качества; 2-й - 84%.
Наудачу взятая из конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена 1-м автоматом.
10/17
9/16
8/15
11/18
57. Задание {{57}} ТЗ № 75
Вероятность изготовления на автоматическом станке стандартной детали равна 0.9. Определить вероятность того, что из 6 наудачу взятых деталей, 4- окажутся стандартными.
0,0984
0,0972
0,0968
0,0942
58. Задание {{58}} ТЗ № 32
Монету подбрасывают 8 раз.
Вероятность того, что 6 раз выпадет герб, равна ...
1/8
1/4
7/64
8/64
59. Задание {{59}} ТЗ № 303
Монету подбрасывают 10 раз. Вероятность того, что герб выпадет хотя бы один раз, равна ...
1023/1024
9/10
980/1000
99/100
60. Задание {{60}} ТЗ № 304
Игральную кость подбрасывают 4 раза. Вероятность того, что шестерка выпадет 2 раза, равна ...
25/216
1/2
1/6
18/144
61. Задание {{61}} ТЗ № 305
Игральную кость подбрасывают 4 раза. Вероятность того, что шестерка выпадет хотя бы 1 раз, равна ...
0,51
0,25
0,75
0,49
62. Задание {{62}} ТЗ № 306
Игральную кость подбрасывают 4 раза. Вероятность того, что шестерка выпадет не более одного раза, равна ...
0,64
0,87
0,48
0,39
63. Задание {{63}} ТЗ № 23
Вероятность рождения мальчика равна 0,51. Тогда вероятность того, что среди 100 новорожденных окажется 50 мальчиков, вычисляется по формуле
64. Задание {{64}} ТЗ № 24
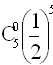
65. Задание {{65}} ТЗ № 26
Монету подбрасывают 8 раз. Вероятность того, что она 6 раз упадет "гербом" вверх, равна
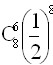
66. Задание {{66}} ТЗ № 27
Вероятность выигрыша по одному лотерейному билету равна 1/7. Тогда вероятность того, что лицо, имеющее шесть билетов, выиграет по двум билетам, равна
67. Задание {{67}} ТЗ № 76
Два равносильных шахматиста играют в шахматы. Чему равна вероятность выиграть 2 партии из 4-х? Ничьи во внимание не принимаются.
3/8
1/2
5/8
5/16
68. Задание {{68}} ТЗ № 77
Два равносильных шахматиста играют в шахматы.
Чему равна вероятность выиграть 3 партии из 6-х?
Ничьи во внимание не принимаются.
5/16
3/8
1/2
5/8
69. Задание {{69}} ТЗ № 78
В семье 5 детей. Найти вероятность того, что среди них 2 мальчика.
(Вероятность рождения мальчика принять равной 0,51)
0,31
0,33
0,36
0,4