Задание 19 (Свойства плотности вероятности и ф-ии распределения. Равномерн. Рас-ние)
205. Задание {{205}} Свойства плотности
Пусть р(х) - плотность вероятности. Тогда функция р(х)
не убывает
не возрастает
неотрицательна
не превосходит единицы
возрастает
убывает
206. Задание {{206}} Свойства функции распр
Пусть F(x) - функция распределения. Тогда F(x)
возрастает
убывает
не превосходит единицы
не возрастает
не убывает
неотрицательна
207. Задание {{207}} Смысл мат ожидания
Математическое ожидание случайной величины - это
ее среднее значение
мера ее рассеяния
ее наибольшее значение
ее наименьшее значение
мера ее отклонения от среднего значения
208. Задание {{208}} Смысл дисперсии
Дисперсия случайной величины - это
ее среднее значение
мера ее рассеяния
ее наибольшее значение
ее наименьшее значение
209. Задание {{209}} Малая дисперсия
Дисперсия некоторой случайной величины мала. Тогда
ее значения группируются вблизи среднего значения
ее значения сильно разбросаны относительно среднего значения
ее среднее значение велико
ее среднее значение мало
210. Задание {{210}} Равномерн. распр.1
Тогда значение ее плотности вероятности p(x) на этом отрезке равно
Эталон(ы) ответа: 1
211. Задание {{211}} Равномерн. распр.2
Тогда значение ее плотности вероятности p(x) на этом отрезке равно
Эталон(ы) ответа: 2
212. Задание {{212}} Равномерн. распр.3
Тогда значение ее плотности вероятности p(x) на этом отрезке равно
Эталон(ы) ответа: 3
213. Задание {{213}} Равномерн. распр.4
Случайная величина равномерно распределена на отрезке [0;1/4]. Тогда значение ее плотности вероятности p(x) на этом отрезке равно
Эталон(ы) ответа: 4
214. Задание {{214}} Равномерн. распр.5
Тогда значение ее плотности вероятности p(x) на этом отрезке равно
Эталон(ы) ответа: 1
Задание 20 (Нормальное распределение)
215. Задание {{215}} Норм. распр.1
Некоторая случайная величина имеет плотность вероятности вида
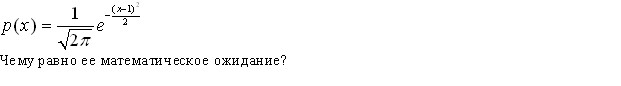
Эталон(ы) ответа: 1
216. Задание {{216}} Норм. распр.2
Некоторая случайная величина имеет плотность вероятности вида
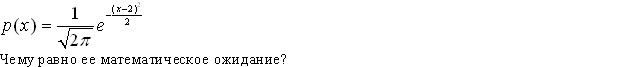
Эталон(ы) ответа: 2
217. Задание {{217}} Норм. распр.3
Некоторая случайная величина имеет плотность вероятности вида
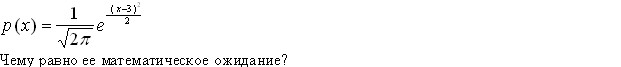
Эталон(ы) ответа: 3
218. Задание {{218}} Норм. распр.4
Некоторая случайная величина имеет плотность вероятности вида
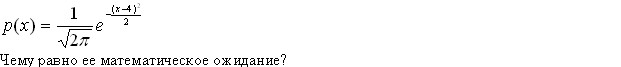
Эталон(ы) ответа: 4
219. Задание {{219}} Норм. распр.5
Некоторая случайная величина имеет плотность вероятности вида
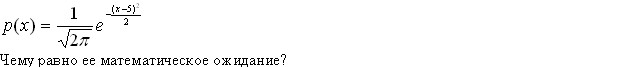
Эталон(ы) ответа: 5
220. Задание {{220}} Норм. распр. дисп.1
Некоторая случайная величина имеет плотность вероятности вида
Эталон(ы) ответа: 2
221. Задание {{221}} Норм. распр. дисп.2
Некоторая случайная величина имеет плотность вероятности вида
Эталон(ы) ответа: 2
222. Задание {{222}} Норм. распр. дисп.3
Некоторая случайная величина имеет плотность вероятности вида
Эталон(ы) ответа: 2
223. Задание {{223}} Норм. распр. дисп.4
Некоторая случайная величина имеет плотность вероятности вида
Эталон(ы) ответа: 2
224. Задание {{224}} Норм. распр. дисп. 5
Некоторая случайная величина имеет плотность вероятности вида
Эталон(ы) ответа: 2