Домашнее задание.

1. Является ли высказывание (X Y) (Y X) тавтологией.

2. Установить эквивалентны ли высказывания.

3. С помощью таблиц истинности доказать законы поглощения и склеивания.

Законы де моргана. Тождественность высказываний. Упрощение формул. План урока.

1. Изучение нового материала.

2. Практическая работа на ЭВМ.

Ход урока.

I. Подача нового материала.

1. Упрощение формул.

Пример 1. Упростить формулу (А+В)· (А+С)

Решение.

1. Раскроем скобки ( A + B ) * ( A + C ) A * A + A * C + B * A + B * C

2. По закону идемпотентности A*A A , следовательно, A*A + A*C + B*A + B*C A + A*C + B*A + B*C

3. В высказываниях А и А*C вынесем за скобки А и используя свойство А+1 1, получим А+А*С+ B*A + B*C A*( 1 + С) + B*A + B*С A + B*A + B*С

4. Аналогично пункту 3. вынесем за скобки высказывание А. A + B*A + B*С A ( 1 + B ) + B С A + B*С Таким образом, мы доказали закон дистрибутивности.

2. Преобразования “поглощение” и “склеивание”

Пример 2. Упростить выражение А+ A*B

Решение. A+A*B A ( 1 + B ) A - поглощение

Пример 3. Упростить выражение A*B+A*

Решение. A*B + A* A ( B + ) A - склеивание

3. Всякую формулу можно преобразовать так, что в ней не будет отрицаний сложных высказываний - все отрицания будут применяться только к простым высказываниям.

Пример 4. Преобразовать формулу так, чтобы не было отрицаний сложных высказываний.

Решение.

1. Воспользуемся формулой де Моргана, получим:

2. Для выражения 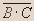применим еще раз формулу де Моргана, получим:

4. Любую формулу можно тождественно преобразовать так, что в ней не будут использованы:

• знаки логического сложения;

• знаки логического умножения,

• будут использованы:

• знаки отрицания и логического умножения

• знаки отрицания и логического сложения.

Пример 5. Преобразовать формулу так, чтобы в ней не использовались знаки логического сложения.

Решение. Воспользуемся законом двойного отрицания, а затем формулой де Моргана.

Пример 6. Преобразовать формулу так, чтобы в ней не использовались знаки логического умножения.

Решение. Используя формулы де Моргана и закон двойного отрицания получим:

5. Замена эквиваленции и импликации на конъюнкцию, дизъюнкцию и отрицание.

До сих пор мы занимались равносильными преобразованиями формул, не содержащих знаков импликации и эквиваленции “ “ и “ “. Сейчас покажем, что всякую формулу, содержащую или , можно заменить равносильной ей формулой, не содержащей этих знаков.

Имеют место следующие равносильности:

X Y Y (1) X Y (2)

Докажем равносильность (1) с помощью таблицы истинности:

X	Y	X Y		Y
0	0	1	1	1
0	1	1	1	1
1	0	0	0	0
1	1	1	0	1

Эквиваленция выражается через конъюнкцию и импликацию

X Y (X Y)*(X Y) (3) Из (3) и (1) получаем X Y ( Y)*( X) * Y* *X X*Y= * X*Y (4)

Эта равносильность выражает эквиваленцию через конъюнкцию, дизъюнкцию и отрицание. Из равносильностей (3) и (2) получаем равносильность

X Y= U , (5) выражающую эквиваленцию через конъюнкцию и отрицание.

Вывод: В алгебре логики всякую логическую функцию можно выразить через другие логические функции, но их должно быть по меньшей мере 2 операции, при этом одной из них обязательно должно быть отрицание.

Все операции можно выразить через конъюнкцию и отрицание, дизъюнкцию и отрицание, импликацию и отрицание. Через эквиваленцию и отрицание остальные операции выразить нельзя.