1.Определение линейного векторного пространства

Из курса аналитической геометрии известно, что любая точка плоскости (при заданной системе координат) определяется двумя координатами, т.е. упорядоченной парой двух вещественных чисел, аналогично и любой вектор на плоскости. Любая точка трёхмерного пространства определяется тремя координатами, а вектор, в пространстве, тремя компонентами. Однако в геометрии, механике и физике приходится изучать такие объекты, для задания которых недостаточно трёх вещественных чисел.

Рассмотрим совокупность шаров в трёхмерном пространстве. Для того, чтобы шар был полностью определён нужно задать координаты его центра и радиус, т.е. задать упорядоченный набор четырёх вещественных чисел, из которых последнее – R – может принимать только положительные значения.

Рассмотрим различные положения твёрдого тела в пространстве. Для его определения нужны: - координаты центра тяжести (3 числа); - направление некоторой фиксирующей оси, проходящей через центр тяжести (2 числа – 2 из 3-х направляющих косинусов) и угол поворота вокруг этой оси. Т.е. система из 6 вещественных чисел.

Эти примеры указывают на целесообразность рассмотрения совокупности всевозможных упорядоченных систем из n совокупностей вещественных чисел.

Введём некоторые понятия.

Упорядоченный набор n чисел , называется n-мерным вектором; где , ( ) – координаты вектора . Целесообразно дать «бескоординатное» определение векторного пространства, не требующее задания векторов упорядоченными наборами чисел. Такое определение – аксиоматическое, в нем ничего не будет сказано о свойствах отдельного вектора, но будут перечислены свойства, которыми должны обладать операции над векторами.

Пусть Р – некоторое числовое поле (оно, в частности, может быть полем вещественных или полем комплексных чисел) и V – некоторое множество, природа элементов которого не важна. Условимся элементы множества V обозначать малыми латинскими буквами а, b, c,..., а числа из Р – малыми греческими буквами .

Пусть во множестве определены:

1) операция сложения, ставящая каждой паре элементов а, b из V в соответствие единственный элемент a+b того же множества V, называемый их суммой;

2) операция умножения на вещественное число, ставящая в однозначное соответствие числу из Р и элементу а из V элемент того же множества V.

Определение: Элементы множества V будут называться векторами, а само V – вещественным линейным (или векторным) пространством, если для указанных операций (1, 2) выполняются следующие свойства, называемые аксиомами линейного пространства:

I. Свойства сложения:

1. коммутативность: а + b = b + а, где а, b произвольные элементы множества V;

2. ассоциативность 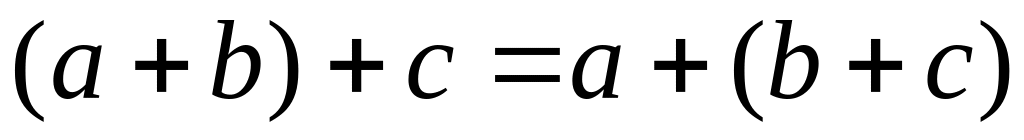для любых элементов a, b, c рассматриваемого множества V;

3. в множестве V существует по меньшей мере один такой элемент 0, называемый нулевым, что для любого а из V;

4. для всякого данного множества существует по меньшей мере один такой элемент , называемый противоположным элементом к а, что .

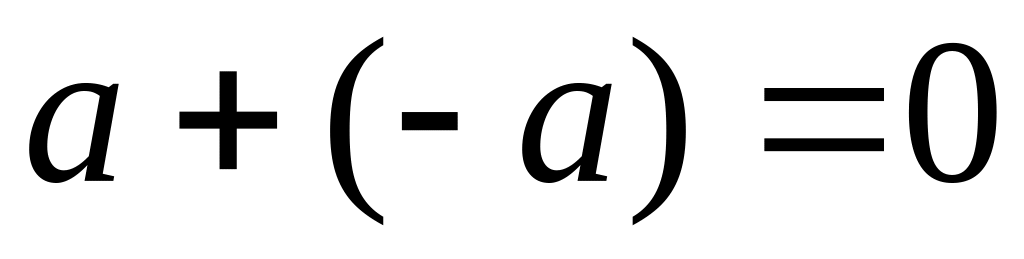II. Свойства умножения:

5. дистрибутивность относительно сложения чисел: если 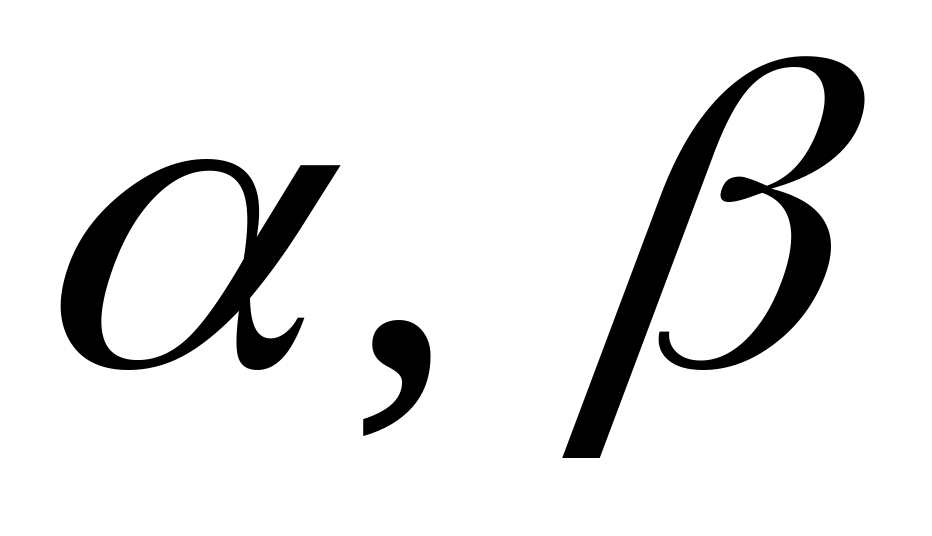– числа из P и а, b произвольные элементы V, то ,

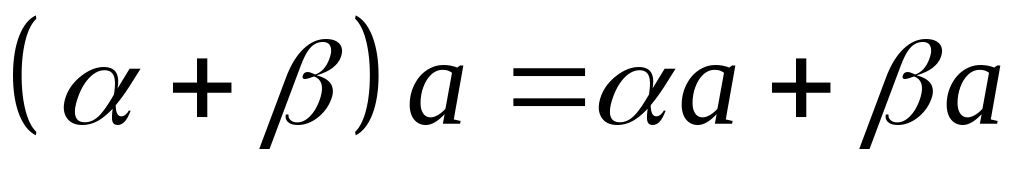6. дистрибутивность относительно сложения векторов: .

7. ассоциативность относительно умножения чисел: если – числа из числового поля P и а – произвольный элемент рассматриваемого множества V, то

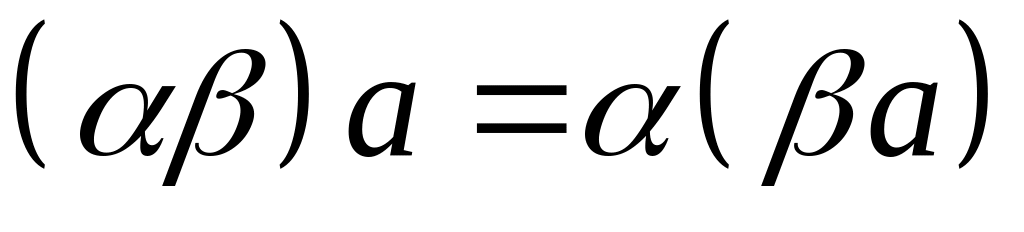
8. для любого элемента и для числа 1 из P справедливо равенство .
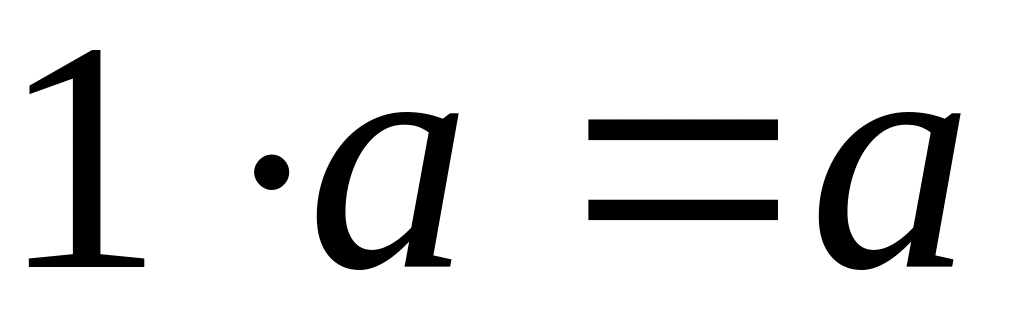