Вопрос 22
Множество - это совокупность, набор элементов, объединенных общими свойствами.
Множества
обозначаются заглавными латинскими
буквами 
,
а элементы множества строчными латинскими
буквами 
.
Запись 
означает,
что есть множество 
с
элементами
,
которые связаны между собой какой-то
функцией 
.
Замечание. Элементы в множество входят по одному разу, т.е. без повторений.
Основные операции:
Принадлежность элемента множеству:
где 
--
элемент и
--
множество (элемент
принадлежит
множеству
).
Непринадлежность элемента множеству:
где -- элемент и -- множество (элемент не принадлежит множеству ).
Объединение множеств:
.
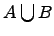Объединением
двух множеств
и 
называется
множество 
,
которое состоит из элементов
множеств
и
,
т.е.
или
Пересечение множеств:
.
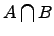Пересечением двух множеств и называется множество , которое состоит из общих элементов множеств и , т.е.
и
Разность множеств:
.
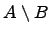Разностью двух множеств и , например, множество минус множество , называется множество , которое состоит из элементов множества , которых нет в множестве , т.е.
и
Симметрическая разность множеств:
.
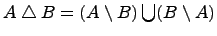Симметрической разностью двух множеств и называется множество , которое состоит из не общих элементов множеств и , т.е.
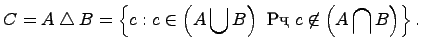
Дополнение множества:
.
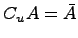Если
предположим, что множество
является
подмножеством некоторого универсального
множества 
,
тогда определяется операция дополнения:
и
Вхождение одного множества в другое множество:
.
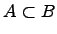Если любой элемент множества является элементом множества , то говорят, что множество есть подмножество множества (множество входит в множество ).
Не вхождение одного множества в другое множество:
.
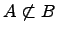Если существует элемент множества , который не является элементом множества , то говорят, что множество не подмножество множества (множество не входит в множество ).
Булевой алгеброй[1][2][3] называется
непустое множество A с
двумя бинарными
операциями 
(аналог конъюнкции), 
(аналог дизъюнкции), унарной
операцией 
(аналог отрицания)
и двумя выделенными элементами: 0 (или
Ложь) и 1 (или Истина) такими, что для
всех a, b и c из
множества A верны
следующие аксиомы:
Сводная таблица свойств и аксиом, описанных выше:
|
|
1 коммутативность переместительность |
|
|
2 ассоциативность сочетательность |
3.1 конъюнкция
относительно дизъюнкции |
3.2 дизъюнкция
относительно конъюнкции |
3 дистрибутивность распределительность |
|
|
4 комплементность дополнительность (свойства отрицаний) |
|
|
5 законы де Моргана |
|
|
6 законы поглощения |
|
|
7 Блейка-Порецкого |
|
|
8 Идемпотентность |
|
|
9 инволютивность отрицания |
|
|
10 свойства констант |
|
|
|
дополнение 0 есть
1 |
дополнение 1 есть
0 |
|
|
|
11 Склеивание |
;
.
;
.
;
.
;
.
;
.
;
.
;
.
.
;
.
;
.
;
.
;
.