
- •2) Основное уравнение молекулярно-кинетической теории идеального газа.
- •3) Уравнение состояния идеального газа
- •4) Закон распространения молекул по скоростям
- •6) Явление переноса в газах. Средняя длина свободного пробега.
- •7)Внутреннее трение газов. Крэффициент внутреннего трения.
- •8) Теплопроводность газов. Распределение энергии по степеням свободы.
- •9) Коэффициент теплопроводности газов
- •10) Стационарная диффузия
- •11) Нестационарное диффузия. Термодинамический метод описания явлений.
- •12) Термодинамические параметры
- •13) Внутренняя энергия и температура термодинамической системы
- •14) Внутренняя энергия. Работа. Теплота
- •15) Первый закон термодинамики
10) Стационарная диффузия
Стационарное уравнение
В случае, когда ставится задача по нахождению установившегося распределения плотности или температуры (например, в случае, когда распределение источников не зависит от времени), из нестационарного уравнения выбрасывают члены уравнения, связанные со временем. Тогда получается стационарное уравнение теплопроводности, относящееся к классу эллиптических уравнений. Его общий вид:
![]()
При
 ,
не зависящем от
,
не зависящем от 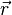 ,
стационарное уравнение диффузии
становится уравнением
Пуассона (неоднородное), или уравнением
Лапласа (однородное, то есть при
,
стационарное уравнение диффузии
становится уравнением
Пуассона (неоднородное), или уравнением
Лапласа (однородное, то есть при  ):
):
![]()
![]()
11) Нестационарное диффузия. Термодинамический метод описания явлений.
Термодинамическая система
Нестационарное уравнение диффузии классифицируется как параболическое дифференциальное уравнение. Оно описывает распространение растворяемого вещества вследствиедиффузии или перераспределение температуры тела в результате теплопроводности.
Одномерный случай
В случае одномерного диффузионного процесса с коэффициентом диффузии (теплопроводности) уравнение имеет вид:
![]()
При постоянном приобретает вид:
![]()
где ![]() —
концентрация диффундирующего вещества,
a
—
концентрация диффундирующего вещества,
a ![]() —
функция, описывающая источники вещества
(тепла).
—
функция, описывающая источники вещества
(тепла).
Трёхмерный случай
В трёхмерном случае уравнение приобретает вид:
![]()
где ![]() — оператор
набла, а
— оператор
набла, а ![]() —
скалярное произведение. Оно также может
быть записано как
—
скалярное произведение. Оно также может
быть записано как
![]()
а при постоянном приобретает вид:
![]()
где ![]() — оператор
Лапласа.
— оператор
Лапласа.
n-мерный случай
![]() -мерный
случай — прямое обобщение приведенного
выше, только под оператором набла,
градиентом и дивергенцией, а также под
оператором Лапласа надо понимать
-мерные
версии соответствующих операторов:
-мерный
случай — прямое обобщение приведенного
выше, только под оператором набла,
градиентом и дивергенцией, а также под
оператором Лапласа надо понимать
-мерные
версии соответствующих операторов:
![]()
![]()
Это касается
и двумерного случая ![]() .
.
Мотивировка
A.
Обычно уравнение диффузии возникает из эмпирического (или как-то теоретически полученного) уравнения, утверждающего пропорциональность потока вещества (или тепловой энергии) разности концентраций (температур) областей, разделённых тонким слоем вещества заданной проницаемости, характеризуемой коэффициентом диффузии (или теплопроводности):
![]() (одномерный
случай),
(одномерный
случай),
![]() (для
любой размерности),
(для
любой размерности),
в сочетании с уравнением непрерывности, выражающим сохранение вещества (или энергии):
![]() (одномерный
случай),
(одномерный
случай),
![]() (для
любой размерности),
(для
любой размерности),
с учетом в случае уравнения теплопроводности ещё теплоёмкости (температура = плотность энергия / удельная теплоемкость).
Здесь источник вещества (энергии) в правой части опущен, но он, конечно же, может быть легко туда помещён, если в задаче есть приток (отток) вещества (энергии).
B.
Кроме того,
оно естественно возникает как непрерывный
предел аналогичного разностного
уравнения, возникающего в свою очередь
при рассмотрении задачи о случайном
блуждании на дискретной решётке
(одномерной или
-мерной).
(Это простейшая модель; в более сложных
моделях случайных блужданий уравнение
диффузии также возникает в непрерывном
пределе). Простейшей интерпретацией
функции ![]() в
этом случае служит количество (или
концентрация) частиц в данной точке
(или вблизи неё), причём каждая частица
движется независимо от остальных без
памяти (инерции) своего прошлого (в
несколько более сложном случае — с
ограниченной по времени памятью).
в
этом случае служит количество (или
концентрация) частиц в данной точке
(или вблизи неё), причём каждая частица
движется независимо от остальных без
памяти (инерции) своего прошлого (в
несколько более сложном случае — с
ограниченной по времени памятью).
Решение
В одномерном
случае фундаментальное решение однородного
уравнения с постоянным — не зависящем
от ![]() и
и ![]() —
(при
начальном условии, выражаемом дельта-функцией
—
(при
начальном условии, выражаемом дельта-функцией ![]() и
граничном условии
и
граничном условии ![]() )
есть
)
есть
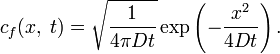
В этом
случае ![]() можно
интерпретировать как плотность
вероятности того, что одна частица,
находившаяся в начальный момент времени
в исходном пункте, через время
перейдёт
в пункт с координатой
.
То же самое — с точностью до множителя,
равного количеству диффундирующих
частиц — относится к их концентрации,
при условии отсутствия или пренебрежимости
взаимодействия диффундирующих частиц
между собой. Тогда (при таких начальных
условиях) средний квадрат удаления
диффундирующих частиц (или соответствующая
характеристика распределения температуры)
от начальной точки
можно
интерпретировать как плотность
вероятности того, что одна частица,
находившаяся в начальный момент времени
в исходном пункте, через время
перейдёт
в пункт с координатой
.
То же самое — с точностью до множителя,
равного количеству диффундирующих
частиц — относится к их концентрации,
при условии отсутствия или пренебрежимости
взаимодействия диффундирующих частиц
между собой. Тогда (при таких начальных
условиях) средний квадрат удаления
диффундирующих частиц (или соответствующая
характеристика распределения температуры)
от начальной точки

В случае
произвольного начального распределения ![]() общее
решение уравнения диффузии представляется
в интегральном виде как свёртка:
общее
решение уравнения диффузии представляется
в интегральном виде как свёртка:
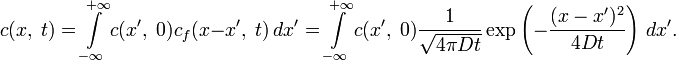 Физические
замечания
Физические
замечания
Так как приближение, реализуемое уравнениями диффузии и теплопроводности, принципиально ограничивается областью низких скоростей и макроскопических масштабов (см. выше), то неудивительно, что их фундаментальное решение на больших расстояниях ведёт себя не слишком реалистично, формально допуская бесконечное распространение воздействия в пространстве за конечное время; надо при этом заметить, что величина этого воздействия так быстро убывает с расстоянием, что этот эффект как правило в принципе ненаблюдаем (например, речь идёт о концентрациях много меньше единицы).
Впрочем, если речь идёт о ситуациях, когда могут быть экспериментально измерены столь маленькие концентрации, и это для нас существенно, нужно пользоваться по меньшей мере не дифференциальным, а разностным уравнением диффузии, а лучше — и более подробными микроскопической физической и статистической моделями, чтобы получить более адекватное представление о реальности в этих случаях.
Термодинамический метод описания явлений.
Для изучения тепловых процессов в естествознании сформировался Термодинамический метод исследования. Он заключается в том, что состояние термодинамической системы задается Термодинамическими параметрами(параметрами системы), характеризующими ее свойства. В качестве таковых обычно выбирают АбсолютнуюТемпературу (температуру по шкале Кельвина – Т), Давление (Р), Молярный объем (объем одного моля вещества –VМ). Параметры связаны друг с другом, поэтому состояние системы можно представить в виде уравнения. Например, для идеального газа массой в один моль эту связь выражает уравнение Менделеева-Клапейрона:
PVМ = RT
Где R = 8,314 Дж/моль * К – универсальная газовая постоянная.
Термодинамика содержит два раздела: равновесная и неравновесная термодинамика. Равновесная термодинамикаизучает процессы в системах, находящихся в равновесном состоянии, а также Процессы, протекающие при нарушении и восстановлении равновесия (например, такие явления, как теплопроводность или диффузия). Равновесное состояниесистемы – состояние, в котором ее параметры при неизменных внешних условиях остаются постоянными сколь угодно долго и одинаковы во всех ее частях. Неравновесная термодинамика описывает явления в закрытых и открытых системах.
Термодинамический метод устанавливает связи между макроскопическими свойствами тел, рассматривая эти свойства как бы снаружи, не вникая в структуру вещества. Он изучает общие закономерности передачи и превращения энергии. Основу термодинамики составляют два фундаментальных закона: первое и второе начала термодинамики, которые являются итогом обобщения практического опыта человечества, поэтому он успешно применяется во всех отраслях естествознания (химии, биологии и др.). Однако, с другой стороны, термодинамический метод ограничен, так как не дает информации о механизме явлений.
Термодинамическая система
Термодинамическая система - совокупность физических тел, которые могут: - энергетически взаимодействовать между собой и с другими телами; а также - обмениваться с ними веществом.
Термодинамическая система: - состоит из большого количества частиц; и - подчиняется в своем поведении статистическим закономерностям, проявляющимся на всей совокупности частиц.
Для термодинамических систем выполняются законы термодинамики
