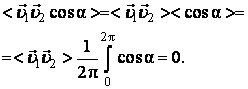6) Явление переноса в газах. Средняя длина свободного пробега.

Явления переноса в газах

• Распространение молекул примеси в газе от источника называется диффузией.

       В состоянии равновесия температура Т и концентрация n во всех точках системы одинакова. При отклонении плотности от равновесного значения в некоторой части системы возникает движение компонент вещества в направлениях, приводящих к выравниванию концентрации по всему объему системы. Связанный с этим движением перенос вещества обусловлен диффузией. Диффузионный поток будет пропорционален градиенту концентрации:

• Если какое-либо тело движется в газе, то оно сталкивается с молекулами газа и сообщает им импульс. С другой стороны, тело тоже будет испытывать соударения со стороны молекул, и получать собственный импульс, но направленный в противоположную сторону. Газ ускоряется, тело тормозится, то есть на тело действуют силы трения. Такая же сила трения будет действовать и между двумя соседними слоями газа, движущимися с разными скоростями. Это явление носит название внутреннее трение или вязкость газа, причём сила трения пропорциональна градиенту скорости:

  .

  (3.1.1)

• Если в соседних слоях газа создана и поддерживается разность температур, то между ними будет происходить обмен тепла. Благодаря хаотическому движению, молекулы в соседних слоях будут перемешиваться и их средние энергии будут выравниваться. Происходит перенос энергии от более нагретых слоев к более холодным телам. Этот процесс называетсятеплопроводностью. Поток тепла пропорционален градиенту температуры:

  .

  (3.1.2)

• В состоянии равновесия в среде, содержащей заряженные частицы, потенциал электрического поля в каждой точке соответствует минимуму энергии системы. При наложении внешнего электрического поля возникает неравновесное движение электрических зарядов в таком направлении, чтобы минимизировать энергию системы в новых условиях. Связанный с этим движением перенос электрического заряда называется электропроводностью, а само направленное движение зарядов - электрическим током.

В процессе диффузии при теплопроводности и электропроводности происходит перенос вещества, а при внутреннем трении – перенос энергии. В основе этих явлений лежит один и тот же механизм – хаотическое движение молекул. Общность механизма, обуславливающего все эти явления переноса, приводит к тому, что их закономерности должны быть похожи друг на друга.

Под средней длиной свободного пробега понимают среднее расстояние, которое проходит молекула между двумя последовательными соударениями.

За секунду молекула в среднем проходит расстояние, численно равное ее средней скорости  . Если за это же время она испытает в среднем   столкновений с другими молекулами, то ее средняя длина свободного пробега   , очевидно, будет равна

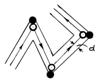
Предположим, что все молекулы, кроме рассматриваемой, неподвижны. Молекулы будем считать шарами с диаметром d. Столкновения будут происходить всякий раз, когда центр неподвижной молекулы окажется на расстоянии меньшем или равном d от прямой, вдоль которой двигается центр рассматриваемой молекулы. При столкновениях молекула изменяет направление своего движения и затем движется прямолинейно до следующего столкновения. Поэтому центр движущейся молекулы ввиду столкновений движется по ломаной линии (рис. 1).

Молекула столкнется со всеми неподвижными молекулами, центры которых находятся в пределах ломаного цилиндра диаметром 2d. За секунду молекула проходит путь, равный   . Поэтому число происходящих за это время столкновений равно числу молекул, центры которых попадают внутрь ломаного цилиндра, имеющего суммарную длину   и радиус d. Его объем примем равным объему соответствующего спрямленного цилиндра, т. е. равным   Если в единице объема газа находится n молекул, то число столкновений рассматриваемой молекулы за одну секунду будет равно

В действительности движутся все молекулы. Поэтому число столкновений за одну секунду будет несколько большим полученной величины, так как вследствие движения окружающих молекул рассматриваемая молекула испытала бы некоторое число соударений даже в том случае, если бы она сама оставалась неподвижной.

Предположение о неподвижности всех молекул, с которыми сталкивается рассматриваемая молекула, будет снято, если в формулу (3.1.2) вместо средней скорости  представить среднюю скорость относительного движения   рассматриваемой молекулы. В самом деле, если налетающая молекула движется со средней относительной скоростью   , то молекула, с которой она сталкивается, оказывается покоящейся, что и предполагалось при получении формулы (3.1.2). Поэтому формулу (3.1.2) следует написать в виде:

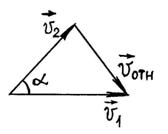
Предположим, что скорости молекул до столкновения были   и   Тогда   Из треугольника скоростей имеем (рис. 2)

Так как углы   и скорости   и   , с которыми сталкиваются молекулы, очевидно, являются независимыми случайными величинами, то среднее

от произведения этих величин равно произведению их средних. Поэтому

С учетом последнего равенства формулу (3.1.4) можно переписать в виде:

так как   Cредняя квадратичная скорость пропорциональна средней скорости,

т. е.   .

Поэтому соотношение (3.1.6) можно представить так:

С учетом последнего выражения формула для средней длины свободного пробега приобретает вид:

Для идеального газа   . Поэтому

Отсюда видно, что при изотермическом расширении (сжатии) средняя длина свободного пробега растет (убывает).

Как было отмечено во введении, эффективный диаметр молекул убывает с ростом температуры. Поэтому при заданной концентрации молекул средняя длина свободного пробега увеличивается с ростом температуры.

Вычисление средней длины свободного пробега для азота (d = 3•10^-10 м), находящегося при нормальных условиях (р = 1,01•10⁵ Па, Т = 273,15 К) дает:  , а для числа столкновений за одну секунду:   . Таким образом, средняя длина свободного пробега молекул при нормальных условиях составляет доли микрон, а число столкновений – несколько миллиардов в секунду. Поэтому процессы выравнивания температур (теплопроводность), скоростей движения слоев газа (вязкое трение) и концентраций (диффузия) являются достаточно медленными, что подтверждается опытом.