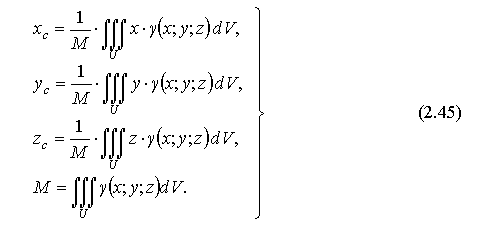Вычисление тройных интегралов в прямоугольных декартовых координатах.
Вычисление тройного интеграла сводится к вычислению трехкратного интеграла.
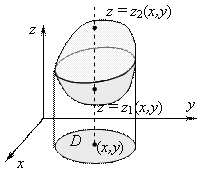
В декартовых координатах область V, правильная в направлении оси OZ, записывается системой неравенств
,
где D –
это проекция области V на
плоскость XOY, а поверхности 
и 
ограничивают
область V соответственно
снизу и сверху (Рис.
6).
Если
двумерную область D также
записать системой неравенств 
,
то трехмерная область V запишется
системой трех неравенств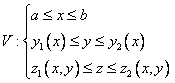 
Тогда тройной интеграл сводится сначала к двойному, а затем к трёхкратному с учётом того, что в декартовых координатах dV = dxdydz;
формула сведения тройного интеграла к трехкратному интегралу имеет следующий вид:
|
|
Вычисление тройных интегралов в цилиндрических координатах.
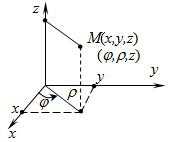
Цилиндрические
координаты точки в пространстве XOYZ—
это ее полярные координаты 
в
плоскости XOY и
координата z.
Связь между декартовыми и цилиндрическими координатами:
Границы изменения цилиндрических координат для всех точек пространства:
|
|
или
Перевод тройного интеграла к цилиндрическим координатам и сведение его к повторному трехкратному интегралу осуществляется следующими действиями:
объем V,
правильный в направлении оси OZ,
проектируется в область 
и
записывается системой неравенств:
;
далее
область 
записывается
неравенствами в полярной системе
координат (Рис.
7) и
составляется бесконечно малый элемент
плоской области в полярных координатах:
,
;
в
подынтегральной функции и в пределах
интегрирования по z делается
переход к переменным 
и 
:
Если выполнить все указанные подстановки, то получится формула вычисления тройного интеграла в цилиндрических координатах:
|
(2) |
Таким
образом, бесконечно
Вычисление тройных интегралов в сферических координатах.
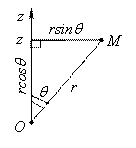
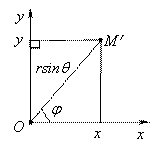
Сферические координаты точки М пространства XOYZ определяются следующим образом (Рис. 8):
r — расстояние точки M от начала координат (длина радиус-вектора точки); r называют сферическим радиусом точки; — угол
между радиус-вектором |
|
и
положительным направлением оси OZ;
— угол между положительным направлением оси OX и проекцией радиус-вектора на плоскость XOY, отсчитываемый против часовой стрелки (полярный угол).
Границы изменения сферических координат для всех точек пространства:
или 
, 
Связь сферических и декартовых координат (выводится геометрически):
|
|
|
Замена переменных в тройном интеграле осуществляется в общем случае по формуле, аналогичной формуле замены переменных в двойном интеграле. В частности, при переходе к сферическим координатам эта формула имеет вид:
,
I — это функциональный определитель Якоби третьего порядка:
,
так как 
поэтому 
.
Таким
образом, 
.
Бесконечно
малый элемент объема в сферических
координатах имеет вид: 
;
формула перевода тройного интеграла к сферическим координатам имеет вид:
|
(3) |
Далее тройной интеграл сводится к трехкратному в соответствии с неравенствами для области V в сферических координатах.
Эффективно переводить в сферические координаты тройной интеграл по областям, в границах которых есть сфера.
Приложения тройных интегралов.
1. Вычисление объёма тела:
2. Вычисление массы тела переменной плотности γ (x; y; z):
3. Координаты центра тяжести тела с постоянной плотностью:
4. Координаты центра тяжести тела с переменной плотностью γ (x; y; z):
7*. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ I и II РОДА.(ЖЕКА)
Сформулировать определения:
1) Криволинейный интеграл I рода.
Криволинейным
интегралом первого рода от скалярной
функции F
вдоль кривой С называется
интеграл вида
.
Где s
- длина дуги.
2) Криволинейный интеграл II рода.
Криволинейным
интегралом второго рода от векторной
функции F
вдоль кривой С называется интеграл вида
- скалярная форма.
- векторная форма.
Сформулировать теоремы и свойства:
1) Условие существования криволинейного интеграла I рода.
Криволинейный интеграл существует, если функция F непрерывна на прямой С.
2) Физический смысл криволинейного интеграла I рода.
3) Геометрический смысл криволинейного интеграла I рода.
Если
функция f(x)
непрерывна и положительна на [a,
b],
то интеграл
представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x)
4) Свойства криволинейных интегралов I рода.
1) Линейность:
2.
Аддитивность: если
в одной точке, то
3.
Монотонность: если
на
,
то
4. Криволинейный интеграл первого рода не зависит от параметризации кривой.
5) Вычисление криволинейного интеграла I рода.
Вычисление криволинейного интеграла 1-го рода сводится к вычислению обычного определенного интеграла от функции переменной t в заданных пределах. С помощью дифференцирования функции.
6) Механический смысл криволинейного интеграла II рода.
Смысл криволинейного интеграла 2 рода – работа по перемещению тела вдоль кривой в поле переменных сил.
7) Свойства криволинейных интегралов II рода.
1. Линейность:
2. Аддитивность:
3.
Монотонность: если
на
,
то
4. Оценка модуля:
8) Вычисление криволинейных интегралов II рода.
9) Связь между криволинейными интегралами I и II рода.
между
криволинейными интегралами первого и
второго рода существует связь:
10) Формула Грина.
11) Условия независимости криволинейного интеграла II рода от пути интегрирования.
Криволинейный
интеграл второго рода от векторной
функции
не
зависит от пути интегрирования,
если P,
Q
и
R
являются
непрерывными функциями в области
интегрирования D
и
в этой области существует скалярная
функция
,
такая, что
12) Приложения криволинейных интегралов I и II рода.
1. Длина дуги АВ плоской или пространственной линии вычисляется по формуле
2. Вычисление площади.
Площадь
S
фигуры,
ограниченной простым замкнутым С,
находится
по формуле
Контур интегрирования проходится так, что ограниченная им область остается слева (положительное направление обхода).
3. Вычисление массы кривой.
Масса
m
материальной
кривой L,
имеющей переменную линейную плоскость
(х,
у),
вычисляется по формуле
4. Координаты центра тяжести
,
,
5.
Работа, совершаемая силой
,
действующей на точку при перемещении
ее по кривой L,
вычисляется по формуле
