4) Разложение функций в ряд Фурье в произвольном интервале.
Для разложения в ряд Фурье непериодической функции, заданной на конечном произвольном промежутке [a,b], надо : доопределить на [b,a+2L] и периодически продолжить, либо доопределить на [b-2L,a] и периодически продолжить.
Разложение периодической функции с периодом L.
Периодическая функция f(x) повторяется при увеличении х на L, т.е. f(x+L)=f(x). Переход от рассмотренных ранее функций с периодом 2π к функциям с периодом L довольно прост, поскольку его можно осуществить с помощью замены переменной.
Чтобы найти ряд Фурье функции f(x) в диапазоне -L/2≤x≤L/2, введем новую переменную u таким образом, чтобы функция f(x) имела период 2π относительно u. Если u=2πх/L, то х=-L/2 при u=-π и х=L/2 при u=π. Также пусть f(x)=f(Lu/2π)=F(u). Ряд Фурье F(u) имеет вид:
Где
коэффициенты ряда Фурье:
Однако чаще приведенную выше формулу приводят к зависимости от х. Поскольку u=2πх/L, значит, du=(2π/L)dx, а пределы интегрирования - от -L/2 до L/2 вместо - π до π. Следовательно, ряд Фурье для зависимости от х имеет вид
где
в диапазоне от -L/2 до L/2 коэффициенты
ряда Фурье,
Пределы
интегрирования могут быть заменены на
любой интервал длиной L, например, от 0
до L)
6. Двойной интеграл: определение, свойства, вычисление, приложение.(артем)
Сформулировать определения:
Определение:
Двойным
интегралом от функции 
по
ограниченной замкнутой области D называется
предел интегральной суммы, построенной
для функции
при
неограниченном увеличении числа
разбиений области D на
ячейки (
) и
при стягивание каждой ячейки в точку (
),
если такой предел существует и не зависит
от способа разбиения области
D
на ячейки, ни от
выбора 
в
каждой из них.
Теорема существования:
Для
всякой непрерывной функции
в
ограниченной замкнутой области 
существует
двойной интеграл: 
Геометрический смысл двойного интеграла:
Пусть тело P в пространстве ограниченно сверху графиком непрерывной и неотрицательной функции z = f(x, y), определенной в области D, цилиндрической поверхностью, направляющей которой служит граница области D, а образующие параллельны оси Oz, и областью D, лежащей в плоскости Oxy. Тело такого вида называют криволинейным цилиндром (цилиндроидом). Двойной интеграл численно равен объему цилиндроида.
Физический смысл двойного интеграла:
объем трехмерного тела в координатах f, x1, x2, ограниченного плоскостью f=0, пределами интегрирования по x1 и по x2 (пределы по x1, x2 также могут быть переменными) и поверхностью, задаваемой в этих координатах функцией f(x1,x2).
Свойства двойных интегралов
Линейное свойство
.
Если функции f (x, y) и g(x, y) интегрируемы в области D, то их алгебраическая сумма также интегрируема в этой области и
Аддитивное свойство по области интегрирования
.
Теорема о среднем. Если функция f (x, y) непрерывна в области D, то в этой области найдется такая точка ( ξ; μ), что
,
где s — площадь фигуры D.
Вычисление двойного интеграла в декартовых координатах
Область D называется правильной относительно оси Ох, если прямая, параллельная этой оси, проходящая через внутреннюю точку области D, пересекает границу области в двух точках. Аналогично определяется правильная область относительно оси Оу.
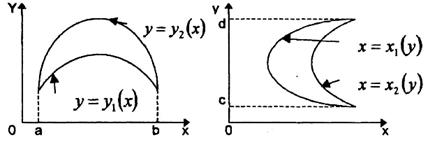
Рисунок 2. Рисунок 3.
Рисунок 2 - Область, правильная, относительно оси Оу Рисунок 3 - Область, правильная, относительно оси Ох
Область D, правильную относительно как Ох, так и Оу, называют просто правильной областью.
Если область D - правильная относительно Оу (рисунок 2), двойной интеграл вычисляется по формуле:
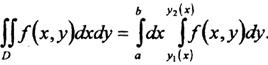
Правую часть формулы (8) называют повторным (двукратным) интегралом. Вычисление повторного интеграла начинаем с вычисления внутреннего интеграла.
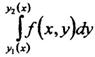
в котором переменную х надо принять при интегрировании за постоянную величину. После подстановки пределов интегрирования в первообразную получаем некоторую функцию, зависящую от х, которую затем интегрируем на отрезке [a,b].
Если область D является правильной относительно оси Ох (рисунок 3), двойной интеграл вычисляется по формуле:
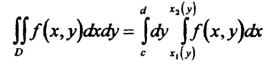
Если область D - просто правильная, можно применять как формулу (8), так и формулу (9). При этом переход от одной формулы к другой называют изменением порядка интегрирования.
Сам процесс перехода от двойного интеграла к повторному и расстановка пределов интегрирования для внешнего и внутреннего интегралов называют приведением двойного интеграла к повторному.
Правило расстановки пределов.
В пределах внутреннего интеграла (интеграла по первой переменной) в общем случае стоят функции второй переменной.
В пределах внешнего интеграла (по второй переменной) стоят постоянные числа. В результате вычисления двойного интеграла получается некоторое постоянное число.
Если
область не является правильной ни
относительно оси Ох, ни относительно
оси Оу, её разбивают на конечное число
областей 
,
правильных относительно одной из осей
и при вычислении применяют свойство 2.
Пример 1.
Вычислить двойной интеграл
двумя способами, если граница области D задана уравнениями:
Решение 1, а
Построив
кривые, получим область D (рисунок
4). Область правильная. Применим
формулу (8). При этом уравнение верхней
границы области х=у2 преобразуем к
виду 
:
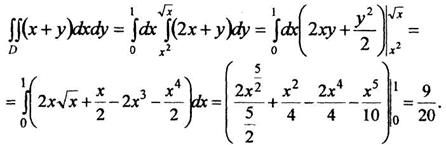
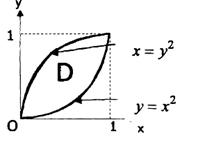
Рисунок 4.- область интегрирования к примеру 1,а
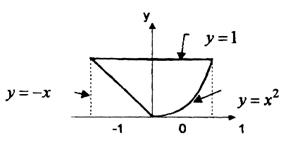
Рисунок 5.- область интегрирования к примеру 1,b
Изменим порядок интегрирования и применим формулу (9):
Решение 1, b
Область D построена на рисунке 5. Область D правильная. Выбираем для интегрирования формулу (9):
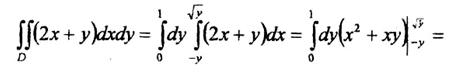
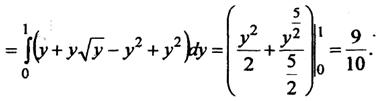
Изменим
порядок интегрирования. При этом нижняя
граница области D задана двумя
аналитическими выражениями 
.
В этом случае область D нужно разбить
на две области Dl, D2 с помощью прямой,
проходящей по оси Оу. На основании
свойства 2 двойного интеграла получаем:
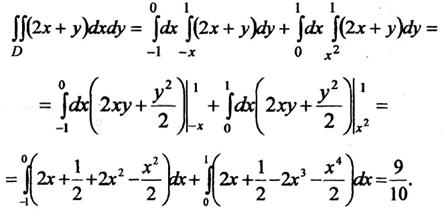
Вычисление двойного интеграла в полярных координатах:
Для вычисления двойного интеграла в полярных координатах применяют тоже правило сведения его к двукратному интегралу.
Если
область 
ограничена
лучами 
и 
,
где 
и
кривыми 
и 
,
где 
,
т.е. область
правильная,
то:
Пример:
Вычислить 
,
где область
–
круг 
Перейдем из декартовой системы координат в полярную:
Область
в
полярной системе координат определяется
неравенствами 
.
Область – круг, преобразовывается в область - прямоугольник. Поэтому:
Приложения двойного интеграла:
1)Объем тела:
,
где 
–
уравнение поверхности, ограничивающей
тело сверху.
2)Площадь плоской фигуры:
– в
декартовой системе координат
– в
полярной системе координат
3)Масса плоской фигуры:
4)Статические моменты:
– относительно
оси 
– относительно
оси 
5)Момент инерции плоской фигуры
– относительно
оси
– относительно
оси
7. ТРОЙНОЙ ИНТЕГРАЛ: ОПРЕДЕЛЕНИЕ, СВОЙСТВА, (НИНА) ВЫЧИСЛЕНИЕ.
Сформулировать определения:
Тройной интеграл.
Тройным интегралом от функции f(x, y, z) по области V называется конечный предел трехмерной интегральной суммы при стремлении к нулю ранга разбиения, порождающего эту сумму (если этот предел существует и не зависит ни от способа разбиения области V на элементарные части, ни от выбора точек на каждой из этих элементарных частей):
Сформулировать теоремы и свойства:
Теорема о существовании тройного интеграла.
Если
функция f (x,y,z)
непрерывная в замкнутой области V,
то 
существует.
Физический смысл тройного интеграла.
Если f (x, y, z)
> 0 в области G,
то тройной интеграл 
представляет
массу тела, занимающего область G и
имеющего переменную плотность 
.
Объем тела, занимающего пространственную
область G находится
по формуле
Свойства тройных интегралов.
1.
Тройной интеграл 
от
обозначения переменных интегрирования
не зависит, т.е.
и т.д.
2. Постоянный множитель можно выносить за знак тройного интеграла:
где k – число. Замена переменных для интегралов Найти уравнение гиперболы Электромагнетизм Радиорелейные системы
3. Тройной интеграл от суммы двух функций равен сумме соответствующих интегралов от слагаемых:
4. Если область V разбита на две области V1 и V2, то
Примечание. Свойства 3 и 4 верны для любого фиксированного числа слагаемых.
5. Если в области V
6. Если в области V
то
7.
8. Теорема
о среднем. Если
функция 
непрерывна
в замкнутой области V, то в этой области
существует точка 
,
такая, что
где V – объем данной области.