3) Теорема Абеля

Если степенной ряд   сходится при x = x1 , то он сходится и притом абсолютно для всех  .

Таким образом, для каждого степенного ряда существует такое положительное число R, что при всех х таких, что   ряд абсолютно сходится, а при всех  ряд расходится. При этом число R называется радиусом сходимости. Интервал (-R, R) называется интервалом сходимости.

4) Способы отыскания интервала и радиуса сходимости степенного ряда.

Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости.  Если интервал сходимости представляется в виде  , где R > 0, то величина R называется радиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно. 

Радиус сходимости может быть найден по формулам:

- Даламбера - Коши

5) Свойства степенных рядов.

1. Сумма степенного ряда есть функция непрерывная в интервале сходимости ряда, т.е.   - непрерывна при a - R< x < a + R.

2. Степенной ряд можно почленно интегрировать в интервале сходимости a - R< x < a + R:

 

3. Степенной ряд можно почленно дифференцировать в интервале сходимости a - R< x < a + R:

.

Более того, степенной ряд в интервале его сходимости можно почленно дифференцировать и интегрировать любое число раз. Отметим, что ряды, полученные почленным интегрированием и дифференцированием степенного ряда, имеют тот же интервал сходимости, что и исходный ряд.

6) Условие разложимости функции в ряд Тейлора.

Для того чтобы бесконечно дифференцируемая в т. функция являлась суммой составленного для нее ряда Тейлора, необходимо и достаточно, чтобы

Используя определение сходящегося ряда и выражение , имеем следующую цепочку:   — сумма

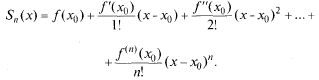
Приведем запись остаточного члена в форме Лагранжа:

  где находится между и х.

7) Разложение основных элементарных функций в ряд Маклорена: ƒ(x) = e^x, ƒ(x) = sin x, ƒ(x) = cos x, ƒ(x) = (1+x)², ƒ(x) = ln(1+x), ƒ(x) = arctg x

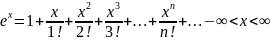
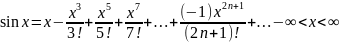
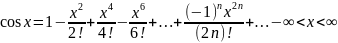
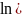
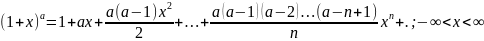
arctgx=x  . 

5. Ряды фурье.

1)Сформулировать определения:

.Тригонометрический ряд.

В математике, тригонометрический ряд — это любой ряд вида:

Тригонометрический ряд называется рядом Фурье функции  , если коэффициенты   и   определяются следующим образом:

где   — это интегрируемая функция.^[1]

Не каждый тригонометрический ряд является рядом Фурье.

.Ряд Фурье.

Ряд Фурье — представление произвольной функции с периодом в виде ряда.

Сформулировать теоремы и свойства:

2) Разложение функций в ряд Фурье на промежутке [-π, π].

Теорема Дирихле: Если функция f(x) непрерывна или имеет конечное число точек разрыва на отрезке [-π, π] и при этом монотонна или имеет конечное число экстремумов на [-π, π] , то ряд Фурье функции f(x) сходится для любых x из [-π, π] и его сумма равна:

1)f(x) для всех точек непрерывности х из интервала [-π, π]

2) для всех точек разрыва

3) при х= и х=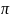

3) Разложение четных и нечетных функций в ряд Фурье на промежутке [-π, π].

Пусть f(x) - четная функция с периодом 2L, удовлетворяющая условию f(-x) = f(x) .

Тогда для коэффициентов ее ряда Фурье находим формулы:

=

=

b_n= 0, где n=1,2, ...

Таким образом, в ряде Фурье для четной функции отсутствуют члены с синусами, и ряд Фурье для четной функции с периодом 2Lвыглядит так:

Пусть теперь f(x) - нечетная функция с периодом 2L, удовлетворяющая условию f(-x) = - f(x).

Тогда для коэффициентов ее ряда Фурье находим формулы:

, где n=1,2, ...

Таким образом, в ряде Фурье для нечетной функции отсутствует свободный член и члены с косинусами, и ряд Фурье для нечетной функции с периодом 2L выглядит так: