20. Множественная корреляция

Множественный коэффициент корреляции ( )

Коэффициент множественной корреляции может быть определен по формулам:

1) =

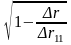
|1 _… |

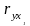
| 1 _… |

∆r= | 1 … |

|………………………|

| _{………………...}1|

Данный определитель-определитель матрицы парных коэффициентов корреляции.

|1 _… |

| 1 _… |

∆r₁₁= |…………………|

| _{… …...}1|

∆r_{11 –} определитель межфакторной связи

Коэффициент множественной корреляции, который вычисляется через определители, называется совокупным коэффициентом корреляции.

2)Также коэффициент множественной корреляции может быть определен через стандартизованные коэффициенты:

= =

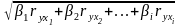
3)Коэффициент множественной корреляции может быть определен:

=

Свойства коэффициента множественной корреляции

1. R находится в интервале от 0 до +1 включительно.

2. R не определяет направление связи.

3. Характеризуется по шкале Чеддока.

4. Величина коэффициента множественной корреляции должна быть больше максимального значения коэффициента парной корреляции:

> (max)

Если коэффициент множественной корреляции практически совпадает с коэффициентом парной корреляции, то дополнительно включенные в уравнение регрессии факторы не имеют значения, поэтому, сравнивая коэффициенты парной и множественной корреляции, можно сделать вывод о целесообразности включения того или иного фактора.

21. Частные уравнения регрессии

Уравнение линейной множественной регрессии (3.2) позволяет построить, так называемые, частные уравнения регрессии, показывающие зависимость результативного признака от отдельного фактора, при исключении влияния остальных факторов, входящих в уравнение множественной регрессии.

Частные уравнения регрессии получаются из уравнения множественной регрессии (3.2) с помощью замены всех факторов, кроме одного на их средние значения:

(3.5)

Уравнения (3.5) можно представить в виде:

= A1+b1*x1

=A2+b2*x2

……

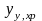=Ap+bp*xp ,

где

В отличие от парной регрессии, частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии.

Частные уравнения регрессии позволяют определить частные коэффициенты эластичности 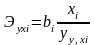, где bi – коэффициенты регрессии для фактора хi в уравнении множественной регрессии; – значение результативного фактора, полученное из частного уравнения регрессии при данном значении фактора хi.

Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.

Средние коэффициенты эластичности для линейной множественной регрессии рассчитываются по формуле и показывают, на сколько процентов в среднем по совокупности изменится результат у от своей величины при изменении фактора х на 1% от своего значения при неизменных значениях других факторов.