17. Проблема мультиколленеарности.

Корреляционные связи есть всегда. Проблема мультиколлинеарности – проблема силы проявления корреляционных связей.

Однозначных критериев мультиколлинеарности не существует.

Строгая мультиколлинеарность нарушает одно из основных правил Гаусса-Маркова и делает построение регрессии полностью невозможным.

Нестрогая мультиколлинеарность затрудняет работу, но не препятствует получению правильных выводов.

Вывод:

1. Последствием мультиколлинеарности является потеря устойчивости вычисления оценок параметров модели

2. Наличие мультиколлинеарности приводит к завышенным значениям СКО оценок

3. Отсутствуют строгие критерии тестирования наличия мультиколлинеарности

4. Подозрением наличия мультиколлинеарности служит большое количество незначимых факторов в модели

5. Для устранения мультиколлинеарности необходимо удалить из спецификации модели факторы, ее вызывающие

6. Для получения спецификации модели, не имеющей мультиколлинеарности можно воспользоваться методом присоединения регрессоров или методом исключения регрессоров

Методы устранения мультикол-ти:

Иногда мультикол-тьне явл-ся серьезной проблемой, чтобы ее выявлять и устраннятть.

Если основная задача модели это прогноз будущ. значения……..признака, то при r наличие мультикол-ти не сказывается на прогнозных кач-вах м-ли.

Единого метода утсранения мультикол-ти не сущ-ет. Сущ-ет несколько методов устранения мультикол-ти:

1. необходимо получить выборку, в кот-ой независимые переменные м/у собой не………..

2. можно увеличить число наблюдений.

проблема решается путем спецификации модели и наложение на эту модель теоритич-их ограничений

18. Отбор факторов при построении множественной регрессии

Включение в уравнение множественной регрессии того или иного набора факторов связано, прежде всего, с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями.

Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1. Факторы не должны быть взаимно коррелированы и, тем более, находиться в точной функциональной связи. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель, и параметры уравнения регрессии оказываются неинтерпретируемыми.

2. Включаемые во множественную регрессию факторы должны существенно влиять на вариацию независимой переменной. Т. е. включаемые в модель факторы должны быть статистически значимыми и существенно улучшать показатель качества модели (например, коэффициент детерминации R2).

Отбор факторов производится на основе качественного теоретико-экономического анализа и обычно осуществляется в две стадии:

– на первой стадии факторы подбираются исходя из сущности проблемы;

– на второй стадии применяются формальные статистические критерии, например, значения t-статистики для соответствующих коэффициентов регрессии.

Наличие высокой корреляции выявляется по значению линейного коэффициента корреляции . Если выполняется условие 0,8 ,то факторные переменные xi , x j находятся в линейной зависимости между собой, а сами переменные xi,x j называются явно коллинеарными.

Значения линейных коэффициентов корреляции rxix j для всевозможных комбинаций переменные xi , x j составляют корреляционную матрицу { rxi x j }.

Для трех факторов матрица { rxix j } принимает вид:

В уравнение регрессии включается только один из коллинеарных факторов, при этом предпочтение отдается тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.

Для преодоления сильной межфакторной корреляции используется ряд подходов:

– исключение из модели одного или нескольких факторов;

– преобразование факторов, при котором уменьшается корреляция между ними;

– переход к совмещенным уравнениям регрессии, т. е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие, например y=a+b1*x1+b2*x2+b3*x3+b12*x1*x2+b13*x1*x3+E, где члены b12*x1*x2 , b13*x1*x3 выражают взаимодействие факторов.

После исключения коллинеарных факторов осуществляется процедура отбора факторов, наиболее влияющих на изменение результативного признака (факторов, включаемых в регрессию). Наиболее широкое применение получили:

●метод исключения;

●метод включения.

В уравнении регрессии включаются только значимые факторы, что проверяется с помощью критерия Стьюдента.

При отборе факторов рекомендуется, кроме всего прочего, пользоваться следующим правилом: число включаемых факторов должно быть в 6–7 раз меньше объема совокупности, по которой строится регрессия.

19. Оценка параметров уравнения множественной регрессии.

Оценка параметров уравнения

1. Выдвигаем нулевую гипотезу:

Н₀=a=0, Н₀= b₁= b₂= b₃=…= b_n=0

2. или

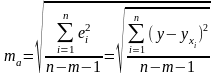
3. Находим t_табл (α,k₂)

4.Сравниваем t_набл и t_табл. Если |t_a, t_b|> t_табл, то нулевая гипотеза отклоняется , коэффициенты уравнения регрессии не равны 0, следовательно статистически значимы. Если наоборот, то равны 0 и незначимы.

5.Доверительные интервалы:

a (b)-m_a(mb)* t_табл ≤a(b)≤ a (b)+m_a(mb)* t_табл

Оценка уравнения регрессии в целом может проводиться на основе множественного коэффициента детерминации:

1. Н₀= =0

2. F_набл=

3. F_табл (α, k_1, k₂)

4. Если F_набл> F_табл , тогда нулевая гипотеза (Н₀) отклоняется и делается вывод о том, что коэффициент детерминации не равен 0, следовательно уравнение регрессии статистически значимо. Если F_набл< F_табл , тогда нулевую гипотезу (Н₀) принимаем и делаем вывод о том, что коэффициент детерминации равен 0, следовательно уравнение регрессии статистически незначимо