6. Линейная модель парной регрессии. Смысл и оценка параметров.
Линейная регрессия сводится к нахождению ур-ия вида ух=а+b*х+е.
у-результативный признак, отклик (зависимая пер-ая)
х-факторный признак, регрессор (независимая переменная)
е – случайное возмущение
а – сводный член
b – коэф-нт регрессии (b>0 связь прямая, b<0 cвязь обратная)
Регрессия – это зависимость сред.значения какой-либо случ.величины от некоторой др.величины или от нескольких величин.
Построение линейной регрессии сводится к оценке её пар-ов - а и b.
Классический подход к нахождению коэф-ов регрессии закл. в методе наименьших квадратов (МНК).
Суть метода закл.в том, что коэф-ты а и b нужно рассчитывать так, чтобы сумма квадратов отклонений фактич.значений у от его теоретич.значений была минимальной.
∑(у-ух)2 min
В ходе мат.преобразований была получена система нормальных ур-ий (СНУ).
Для ур-ия прямой СНУ будет иметь вид:
а
=
;
Для нахождения коэффициентов a и b в уравнении модели парной регрессии можно использовать формулы:
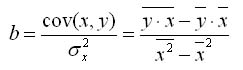
7. Оценка существенности пар-ов регрессии. Смысл и оценка пар-ов.
1. Выдвигаем нулевую гипотезу о статистической незначимости коэф-та регрессии и ур-я регрессии в целомН0: в=0
2. Находим наблюдаемое значение F-критерия Фишера: F набл=Д факт/ Дост.
3.Теорема о разложении дисперсии: общая сумма квадратов отклонений (СКО) признака У от его среднего значения будет раскладываться на 2 части: объясненная и не объясненная
СКО общая=СКО факт.+СКО ост.
4.Число степеней свободы – число независимого признака (варьируемых значений). Обозначается df:
df для СКО (факторная) = k1=m=1, df для СКО (общая) = n-1, df для СКО (остаточная) = k2=n-m-1=n-2
Если разделить сумму квадратов отклонений (СКО) на число степеней свободы (ЧСС), то получим дисперсию на одну степень свободы:
Добщ=
=,
Дфакт=
,
Добщ=
Далее рассчитываем Fнабл и определяем табличное значение этого критерия.
Табличное значение F-критерий Фишера – это максимально возможное значение этого критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости α
Fтабл (α,1, k2)
α=1-Y – уровень значимости (это вероятность отвергнуть принятую гипотезу при условии, что она верна)
Y-доверительная вероятность попадания оцениваемого параметра в интервал. Обычно Y берется близкой к 1 (0,95 или 0,99).
α =0,05 или α =0,01
Далее сравниваем наблюдаемое и табличное значения F-критерия Фишера:
Если Fнабл> Fтабл , тогда нулевая гипотеза (Н0) отклоняется и делается вывод о том, что коэффициент регрессии не равен 0, следовательно уравнение регрессии статистически значимо.
Если Fнабл< Fтабл , тогда нулевую гипотезу (Н0) принимаем и делаем вывод о том, что коэффициент регрессии равен 0, следовательно уравнение регрессии статистически незначимо.
Схема дисперсионного анализа
Компоненты дисперсии |
ЧСС, df |
СКО |
СКО/ЧСС |
F-критерий Фишера |
|
Fнабл |
Fтабл |
||||
Общая |
n-1 |
|
|
|
|
Факторная |
k1=m=1 |
|
|
|
|
Остаточная |
k2=n-m-1 |
|
|
|
|