Медианный шаг
Это время, в теч. кот-го с момента t будет реализована половина общего воздействия фактора на результат.
41.Харак-ка модели с распределенным лагом.
Модели с распределенными лагами- это модели, содержащие в качестве лаговых переменных, лишь независимые переменные.
Модель имеет следующий вид:
,где
● p- конечное число.
Модель говорит о том, что если в некоторый момент времени t происходит изменение х, то это изменение будет влиять на значения у в течение р последующих моментах времени
● Коэффициент - краткосрочный мультипликатор при переменной , т.к. характеризуют изменение ср. значения при изменении факторов на 1 ед-цу в некоторый фиксированный момент времени t.
В момент времени t+1 совокупное воздействие фактора х на рез-т у составим …т.о. любую сумму коэф-тов называют промежуточным мультипликатором.
Сумма всех коэффициентов называется долгосрочным мультипликатором:
Долгосрочный мультипликатор харак-ет изменение у под воздействием единичного изменения х в каждом из моментов времени.
Относительные коэф-ты модели с распределенным лагом определяется по формуле:
Если все коэф-ты β имеют одинаковые знаки, то для любого j-того значения:
0<β <1
=1
Значение β является весами для соответствующих коэф-тов .
Каждый из них измеряет долю общего изменения у, приходящегося на моменты t+j.
Зная величину β можно определить:
ср. лаг, кот-ый рассчитывается по формуле сред.арифметическое:
Он означает период в теч. которого происходит изменение рез-та, от изменения х в момент t. Чем меньше х→ тем быстрее воздействие.
Медианный шаг
Это время, в теч. кот-го с момента t будет реализована половина общего воздействия фактора на результат.
42. Метод Койка и Лаги Алмон
Предположим, что для описания некоторого процесса используется модель с бесконечным лагом вида:
Предполагается геометрическая структура лага, при которой воздействие лаговых значений фактора на результат уменьшается при увеличении лага в геометрической прогрессии.
Койк предположил,
что существует некоторый постоянный
темп λ (от 0 до 1) уменьшения во времени
лаговых воздействий фактора на результат.
Если, например, в период t результат
изменился под воздействием фактора в
этот же период времени на b0 ед., то под
воздействием изменения фактора, имевшего
место в период (t-1), результат изменится
на 
ед.;
в период (t-2) – на 
ед.,
и т.д. для некоторого периода 
это
изменение результата составит 
.
В более общем
виде можно записать: 
Выразим с помощью
этих соотношений в модели 
все
коэффициенты 
через 
и 
В
результате некоторых преобразований
(заменим (1), возьмем период (t-1) (2), умножим
обе части на 
(3),
из (1) вычтем (3)) получаем модель Койка:
где 
Полученная модель есть модель двухфакторной линейной регрессии (точнее - авторегрессии). Определив ее параметры, мы найдем λ и оценки параметров a и b0 исходной модели. Далее с помощью соотношений несложно определить параметры b1,b2,…модели. Отметим, что применении обычного МНК к оценке параметров модели приведет к получению смещенных оценок ее параметров ввиду наличия в этой модели в качестве фактора лаговой результативной переменной yt-1.
Описанный выше алгоритм получил название преобразования койка. Это преобразование позволяет перейти от модели с бесконечными распределенными лагами к модели авторегрессии, содержащей две независимые переменные xt и yt-1.
Несмотря на бесконечное число лаговых переменных в модели, геометрическая структура лага позволяет определить величины среднего и медианного лагов в модели Койка.
Средний лаг: 
Нетрудно заметить,
что при 
средний
лаг 
а
при 
средний
лаг 
т.е.
воздействие фактора на результат в
среднем занимает менее одного периода
времени. Величину 
интерпретируют
обычно как скорость, с которой происходит
адаптация результат во времени к
изменению факторного признака.
Медианный лаг в
модели Койка равен: 
Метод Алмона
Рассмотрим общую
модель с распределенным лагом, имеющую
конечную максимальную величину лага 
,
которая описывается соотношением: 
В методе Алмона
предполагается, что в исследуемой
модели имеет место полиномиальная
структура лага, т.к. зависимость
коэффициентов регрессии 
от
величины лага описывается полиномом
k-й степени. Таким образом, лаги
Алмон –
лаги, структуру которых можно описать
с помощью полиномов.
Формально модель
зависимости коэффициентов
от
величины лага j в
форме полинома можно записать в следующем
виде: 
Тогда
каждый из коэф-ов
модели
можно выразить след. обр.:
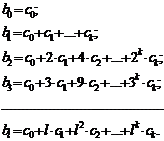
Тогда модель с
распределенным лагом примет вид 
где 
Процедура применения метода Алмон для расчета параметров модели с распределенным лагом проводится по следующей схеме:
1.Устанавливается
макс. величина лага 
2.Определяется степень полинома k, описывающего структуру лага.
3. Рассчитывается значение переменных с z0 до zk.
4. Определяются
параметры уравнения линейной регрессии
5.Рассчитываются параметры b исходной модели с распределенным лагом с помощью ранее найденных соотношений.
Проблемы применения метода Алмон:
- величина лага должна быть известна заранее; при определении лучше исходить из максимально возможного лага;
- необходимо установить степень полинома (должна быть на 1 больше числа экстремумов в структуре лага);
- переменные z, определяемые как линейные комбинации исходных переменных х, коллелируют между собой, если существует высокая связь между исходными переменными х.
Преимущества метода Алмон:
- он достаточно универсален и может быть применен для моделирования процессов, которые характеризуются разнообразными структурами лагов;
- при относительно небольшом количестве переменных можно построить модели со степенью полинома 2 или 3, которые не приводят к потере значительного числа степеней свободы.
- можно построить модели с распределенным лагом любой длины.