
- •1. История развития. Этапы становления.
- •2.Определение (предмет) эконометрики.
- •3. Эконометрический метод и этапы эк-го исследования.
- •4. Измерения в эк-ке.
- •5. Парная регрессия и корреляция. Способы задания уравнения парной регрессии.
- •6. Линейная модель парной регрессии. Смысл и оценка параметров.
- •7. Оценка существенности пар-ов регрессии. Смысл и оценка пар-ов.
- •8. Корреляция и детерминация для линейной регрессии.
- •9. Прогноз по линейному ур-ию регрессии.
- •10. Средняя ошибка аппроксимации
- •11. Нелин.Регрессиия. Классы нелин.Регрессий. Нелин.Регрессия отн-но вкл-ых в анализ объясняющих пер-ых и по оцениваемым пар-ам.
- •2) Нелин.Рег-ия по оцениваемому коэф-ту.
- •12. Корреляция и детерминация для нелинейной регрессии (дисперс-й ан-з)
- •13. Коэффициенты эластичности для разных видов регрессионных моделей.
- •1. Выдвигаем нулевую гипотезу:
- •2. Наблюдаемое значение f-критерия Фишера (Fнабл) определяется по формуле:
- •3. Fтабл (α, k1, k2)
- •4. Сравниваем наблюдаемое и табличное значения. Делаем вывод:
- •15. Оценка адекватности модели
- •16. Множественная регрессия (спецификация модели).
- •17. Проблема мультиколленеарности.
- •18. Отбор факторов при построении множественной регрессии
- •20. Множественная корреляция
- •21. Частные уравнения регрессии
- •22. Частные коэффициенты корреляции
- •23. Оценка надежности результатов множественной регрессии и корреляции.
- •24. Частный f-критерий Фишера ( ) для уравнения множественной регрессии
- •26. Фиктивные переменные во множественной регрессии.
- •27, 28. Предпосылки мнк: гомоскедастичность, гетероскедастичность, автокорреляция остатков.
- •29. Метод наименьших квадратов. Обобщенный мнк.
- •I. Модель в натуральном и стандартизованном масштабе:
- •Множественная модель в натуральном масштабе (общий вид) запишется так:
- •Модель множественной регрессии в стандартизованном масштабе.
- •Мнк для модели в общем виде:
- •Мнк для модели в стандартизованном масштабе:
- •30. Общие понятия и необходимость использования систем эконометр-их уравнений. Формы и составляющие систем эконометрич-х уравнений.
- •31. Формы и составляющие систем эконометрич-х уравнений
- •32. Проблема идентификации. Необходимое и достаточное условие идентифицируемости
- •33. Методы оценки параметров систем уравнений: косвенный, двушаговый и трехшаговый методы.
- •34. Основные элементы временного ряда.
- •35. Автокорреляция уровней временного ряда и выявление его струк-ры.
- •36. Моделирование тенденции временного ряда
- •37. Моделирование сезонных и циклич колебаний
- •38.Автокорреляция в остатках. Критерий Дарбина-Уотсона
- •39. Методы исключения тенденции.
- •2 Основных метода:
- •1)Метод отклонения от тренда.
- •2)Метод последовательных разностей.
- •40. Динамические эконометрические модели
- •1.Харак-ка и интерпретация параметров модели с распределенным лагом.
- •Медианный шаг
- •41.Харак-ка модели с распределенным лагом.
- •Медианный шаг
- •42. Метод Койка и Лаги Алмон
2 Основных метода:
1)Метод отклонения от тренда.
*Предположим, имеются 2 компонента (2 ряда динамики) yt и xt, кот содержат трендовую и случайную компоненты. Проведя аналитич. выравнивание по каждому из этих рядов мы найдем параметры соответствующих уровней трендов и найдем их расчетные ур-ни yt; xt.
Устранить влияние тенденции можно путем вычитания этих расчетных моделей (значений) из фактических значений этого уровня ряда. Такую процедуру осуществляют для каждого временного ряда в модели.
2)Метод последовательных разностей.
*При исключении автокорреляции данным методом, подвергаются обработке методы наименьших квадратов не сами уровни исхдных рядов yt,yt+1,yt+2….yt+n; хt,хt+1,хt+2….хt+n, а последовательные разницы между ними.
⌂y1= yt- yt-1
⌂y2= yt-1-yt-2
⌂y3=yt-k-yt-k-1
⌂x1=xt-xt-1
⌂x2=xt-1-xt-2
⌂x3=xt-k-xt-k-1
2.группа. – это методы, основанные на изучении взаимосвязи исходных уровней рядов динамики, при воздействии фактора времени на зависимую и независимые переменные модели.
Метод включения в ур-ие регрессии фактора времени.
*Этот прием широко используется в анализе временных рядов, когда тенденции фиксируются через включение факторов времени в качестве независимой переменной и наз-ся введение факторов времени в ур-е регрессии.
yt=a+b1x1+b2t+Et
Преимущества данного метода перед предыдущем в том, что он позволяет учесть всю информацию, содержащуюся в исходных данных. Кроме того, модель строится по всей совокупности данных за рассматриваемый период, в отличие от метода последовательных разностей, кот приводят к поте числа наблюдений.
Параметры а и b в модели с включением факторов времени опред-ся методом наименьших квадратов.
40. Динамические эконометрические модели
Динамические модели- это модели, построенные по временным рядам, кот-е характеризуются каждым моментом времени t в отдельности, а не всем периодом, для кот-го строится модель.
Эконометрическая модель считается динамической, если в данный момент времени t она учитывает значение входящих в нее переменных, относящихся как к текущему, так и к предыдущим моментам времени, т.е модель учитывает и отражает динамику, исследуемых переменных за каждый момент времени.
Величина l наз-ся лагом, характеризующая запаздывание воздействия фактора на результат.
Переменные, влияние кот-х характеризуется определенным запаздыванием, называются лаговые переменные.
Динамические модели классифицируются на:
модели с распределенными лагами
авторегрессионные модели
1.Харак-ка и интерпретация параметров модели с распределенным лагом.
Модели с распределенными лагами- это модели, содержащие в качестве лаговых переменных, лишь независимые переменные.
Модель имеет следующий вид:
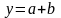
 ,где
,где
● p- конечное число.
Модель говорит о том, что если в некоторый момент времени t происходит изменение х, то это изменение будет влиять на значения у в течение р последующих моментах времени
● Коэффициент
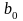 -
краткосрочный мультипликатор при
переменной
-
краткосрочный мультипликатор при
переменной
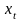 ,
т.к. характеризуют изменение ср. значения
,
т.к. характеризуют изменение ср. значения
 при изменении факторов
на
1 ед-цу в некоторый фиксированный момент
времени t.
при изменении факторов
на
1 ед-цу в некоторый фиксированный момент
времени t.
В
момент времени t+1
совокупное воздействие фактора х
на рез-т у
составим
 …т.о.
любую сумму коэф-тов называют промежуточным
мультипликатором.
…т.о.
любую сумму коэф-тов называют промежуточным
мультипликатором.
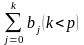
Сумма всех коэффициентов называется долгосрочным мультипликатором:
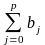
Долгосрочный мультипликатор харак-ет изменение у под воздействием единичного изменения х в каждом из моментов времени.
Относительные
коэф-ты модели с распределенным лагом
определяется по формуле:
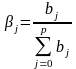
Если все коэф-ты β имеют одинаковые знаки, то для любого j-того значения:
0<β <1
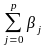 =1
=1
Значение
β
является весами для соответствующих
коэф-тов
 .
.
Каждый из них измеряет долю общего изменения у, приходящегося на моменты t+j.
Зная величину β можно определить:
ср. лаг, кот-ый рассчитывается по формуле сред.арифметическое:

Он означает период в теч. которого происходит изменение рез-та, от изменения х в момент t. Чем меньше х→ тем быстрее воздействие.
