38.Автокорреляция в остатках. Критерий Дарбина-Уотсона
Автокорреляция остатков- это автокор-ция остатков, рассматриваемых в виде временного ряда, содержащих тенденцию или периодические колебания.
Причины автокор-ции остатков:
ошибки измерения в значениях результ-го признака
неправильная спецификация м-ли. Т.е модель может не включать фактор, кот-й оказывает существенное воздействие на рез-т и влияние кот-го отражается в остатках, вследствие чего последние могут оказаться автокореляц-ми. Очень часто таким фактором выступает фактор времени.
Существует 2 наиболее распространенных метода определения автокор-ции остатков:
Построение графика в зависимости остатка от времени и визуальное определение наличия либо отсутствия автокорел-ции.
Критерий Дарбина-Уотсона- это отношение суммы квадрата разностей последовательных значений остатка к остаточной сумме квадрата по модели регрессии:
Формула определения коэф-та автокор-ции 1-го порядка:
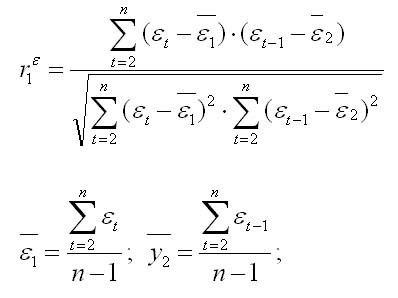
При больших значениях объема выборки сущ-ют следующие соотношения м/у критерием Д.-Уотсона и коэф-том автокор-ции остатка 1-го порядка:
d=
2*(1-r
)
Т.О если в остатках сущ-ет:
|
Полная автокор-ция остатков 1го порядка |
Критрий д.-уотсона |
Полная положит-ая автокорр-ция |
r =1 |
4(0) |
Полная отриц-я автокор-ция |
r =-1 |
4 |
Автокор-ция остатков отсутствует |
r =0 |
2 |
Алгоритм выявления автокор-ции остатков:
1.Выдвигаются гипотезы о том, что:
Н
-
Автокор-ция остатков отсутствует
Н - положит-ая автокорр-ция остатков
Н
-
отрицат-я автокор-ция остатков
2.По
спец-ым таблицам определяются фактические
значения критерия d
и d
для заданного числа наблюдений n,
кол-ва независимых переменных m
и заданного уровня значимости.
3. По этим значениям числовой промежуток от 0 до 4 разбивают на пять отрезков.
4. Расчетные значения критерия Д.-Уотсона сравниваются с табличными и принятие или отклонение каждой из гипотез осущ-ся след-щим образом:
Если фактич-ое значение критерия Д.Уотсона попадает в зону неопределенности, то на практике предполагают существование автокор-ции остатков не ясного харак-ра и отклоняет нулевую гипотезу Н .
Ограничение на применение критерия Д.-Уотсона :
1. Данный критерий не применим, включающим в кач-ве независимых переменных плановые знач-я результативного признака.
2. Методика расчета и использования критерия Д.-Уотсона направлена только на выявление автокор-ции остатков 1го порялка.
3. Критерий Д.-Уотсона дает достоверные рез-ты только для больших выборов.
39. Методы исключения тенденции.
Сущность всех методов заключается в устранении воздействия фактора времени на рез-т, т.е. на формирование уровней ряда.
Такие методы делятся на 2 группы:
1.группа. Это методы, основанные на преобразование уровней исходного ряда в новые переменные, не содержащие тенденции, кот используются в дальнейшем для анализа взаимосвязи, изучаемых рядов динамики.