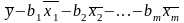- •1. История развития. Этапы становления.
- •2.Определение (предмет) эконометрики.
- •3. Эконометрический метод и этапы эк-го исследования.
- •4. Измерения в эк-ке.
- •5. Парная регрессия и корреляция. Способы задания уравнения парной регрессии.
- •6. Линейная модель парной регрессии. Смысл и оценка параметров.
- •7. Оценка существенности пар-ов регрессии. Смысл и оценка пар-ов.
- •8. Корреляция и детерминация для линейной регрессии.
- •9. Прогноз по линейному ур-ию регрессии.
- •10. Средняя ошибка аппроксимации
- •11. Нелин.Регрессиия. Классы нелин.Регрессий. Нелин.Регрессия отн-но вкл-ых в анализ объясняющих пер-ых и по оцениваемым пар-ам.
- •2) Нелин.Рег-ия по оцениваемому коэф-ту.
- •12. Корреляция и детерминация для нелинейной регрессии (дисперс-й ан-з)
- •13. Коэффициенты эластичности для разных видов регрессионных моделей.
- •1. Выдвигаем нулевую гипотезу:
- •2. Наблюдаемое значение f-критерия Фишера (Fнабл) определяется по формуле:
- •3. Fтабл (α, k1, k2)
- •4. Сравниваем наблюдаемое и табличное значения. Делаем вывод:
- •15. Оценка адекватности модели
- •16. Множественная регрессия (спецификация модели).
- •17. Проблема мультиколленеарности.
- •18. Отбор факторов при построении множественной регрессии
- •20. Множественная корреляция
- •21. Частные уравнения регрессии
- •22. Частные коэффициенты корреляции
- •23. Оценка надежности результатов множественной регрессии и корреляции.
- •24. Частный f-критерий Фишера ( ) для уравнения множественной регрессии
- •26. Фиктивные переменные во множественной регрессии.
- •27, 28. Предпосылки мнк: гомоскедастичность, гетероскедастичность, автокорреляция остатков.
- •29. Метод наименьших квадратов. Обобщенный мнк.
- •I. Модель в натуральном и стандартизованном масштабе:
- •Множественная модель в натуральном масштабе (общий вид) запишется так:
- •Модель множественной регрессии в стандартизованном масштабе.
- •Мнк для модели в общем виде:
- •Мнк для модели в стандартизованном масштабе:
- •30. Общие понятия и необходимость использования систем эконометр-их уравнений. Формы и составляющие систем эконометрич-х уравнений.
- •31. Формы и составляющие систем эконометрич-х уравнений
- •32. Проблема идентификации. Необходимое и достаточное условие идентифицируемости
- •33. Методы оценки параметров систем уравнений: косвенный, двушаговый и трехшаговый методы.
- •34. Основные элементы временного ряда.
- •35. Автокорреляция уровней временного ряда и выявление его струк-ры.
- •36. Моделирование тенденции временного ряда
- •37. Моделирование сезонных и циклич колебаний
- •38.Автокорреляция в остатках. Критерий Дарбина-Уотсона
- •39. Методы исключения тенденции.
- •2 Основных метода:
- •1)Метод отклонения от тренда.
- •2)Метод последовательных разностей.
- •40. Динамические эконометрические модели
- •1.Харак-ка и интерпретация параметров модели с распределенным лагом.
- •Медианный шаг
- •41.Харак-ка модели с распределенным лагом.
- •Медианный шаг
- •42. Метод Койка и Лаги Алмон
27, 28. Предпосылки мнк: гомоскедастичность, гетероскедастичность, автокорреляция остатков.
1. Случайные остатки
Если на графике получена горизонтальная полоса, то остатки представляют собой случайные величины и применение МНК оправдано.
Если нет, то необходимо применять др. функцию, либо вводить дополнит. информацию.
2. Нулевая ср. величина остатков:
E=
(y -
-
 )=0,
независимая от x
)=0,
независимая от x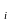
Если
остатки на графике расположены в виде
горизонтальной полосы, то они независимо
от значений x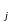 .
.
Если график показывает наличие зависимости от E и x , то модель неадекватна.
3. Гомоскедастичность, т.е. дисперсия каждого отклонения E одинаково для всех значений x .
Если условия не соблюдаются, то имеет место гетероскедастичность.
4. Отстутсвие автокорр-ции остатков:
Автокорреляция остатков означает наличие корреляции м/у остатками текущих и предыдущих наблюдений .
Отсутствие автокорр-ции остаточных величин обеспечивает состоятельность и эффективность оценок коэф-тов регрессии
5. Остатки подчиняются нормальному распределнию.
29. Метод наименьших квадратов. Обобщенный мнк.
I. Модель в натуральном и стандартизованном масштабе:
Множественная модель в натуральном масштабе (общий вид) запишется так:
yx=f (x1,x2,…,xn)
yx=a+b1x1+b2x2+…+bmxm+E
yx-расчетные значения результата (отклик);
x1,x2,…,xm – независимые переменные (регрессор)
b1,b2,…,bm – коэффициенты уравнения.
Для любой регрессионной модели должны выполняться условия Гаусса-Маркова, причем:
M (Ei)=0 – математическое ожидание случайных ошибок должно быть равно 0.
D (Ei)=const. Дисперсия случайных ошибок должны быть постоянной.
Случайные ошибки не ковариируют между собой:
сov (Ei-1;Ei)=0, причем i-1 не равно i.
Случайная величина подчиняется нормальному закону распределения.
Модель множественной регрессии в стандартизованном масштабе.
Построение модели регрессии в стандартизованном (нормированном) масштабе означает, что все переменные, входящие в модель должны стандартизоваться по специальным формулам: данный процесс устанавливаетя для каждой переменной её среднее значение по выборке.
Единицей измерения стандартизованной переменной является её среднеквадратическое отклонение:
ty=β1tx1+ β2tx2+…+ βmtxm+E
ty, tx1, tx2, …, txm – стандартизованные переменные;
β1, β2, …, βm – стандартизованные коэффициенты уравнения регрессии. Данные коэффициенты показывают, насколько единиц в среднем изменится результат, если соответствующий фактор х изменится на 1 единицу при неизменном среднем уровне других факторов.
Результативная переменная у переводится в стандартизованный вид по формуле:
ty=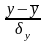
Факторная переменная переводится по той же формуле, только вместо у – xi
Классический подход к оценке коэффициентов уравнения основан также на методе наименьших квадратов (МНК):
Мнк для модели в общем виде:
СНУ для моделей множественной регрессии имеют вид:
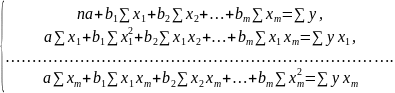
b1=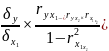
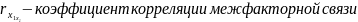
b2=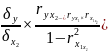
bm=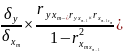
a=