8.Уравнение Клапейрона-Клаузиуса. Фазовые диаграммы. Тройная точка

Клапейрона-Клаузиуса термодинамическое уравнение относится к процессам перехода вещества из одной фазы в другую (испарение, плавление, сублимация, полиморфное превращение и др.). Согласно К.-К. у., теплота фазового перехода (например, теплота испарения, теплота плавления) при равновесно протекающем процессе определяется выражением , (1) где Т-темп-ра перехода (процесс изотермический), dp/dT-значение производной от давления по температуре при данной температуре перехода, (V2-V1)-измен-е объёма вещества при переходе его из первой фазы во вторую. Первоначально уравнение было получено из анализа Карно цикла для конденсирующегося пара, находящегося в тепловом равновесии с жидкостью. Клаузиус усовершенствовал уравнение и распространил его на др. фазовые переходы. К.- К. у. применимо к любым фазовым переходам, сопровождающимся поглощением или выделением теплоты (т. н. фазовым переходом 1 рода), и является прямым следствием условий фазового равновесия.В частности, с его помощью рассчитывают теплоты испарения, экспериментальное опред-е которых сопряжено со значительными трудностями.К.-К. у. является дифференциальным уравнением кривой фазового равновесия в переменных р,Т.Фазовая диаграмма, графическое изображение соотношений между параметрами состояния темп-ры(давлением и др.) и её составом. В простейшем случае, когда сис-ма состоит только из одного компонента, ф. д. представляет собой трёхмерную пространственную фигуру, построенную в трёх прямоугольных координатных осях, по которым откладывают температуру (Т), давление (p) и мольный объём (v). Пользование объёмной ф.д. неудобно вследствие её громоздкости; поэтому на практике применяют проекцию ф.д. на одну из координатных плоскостей, обычно на плоскость p-Т. Тройная точка в термодинамике, точка на диаграмме состояния, соответствующая равновесному сосуществованию трёх фаз вещества.

9. Понятие о физической кинетике. Время релаксации. Эффективное сечение рассеяния. Средняя длина свободного пробега

Физическая кинетика - микроскопическая теория процессов в неравновесных средах. В кинетике методами квантовой или классической статистической физики изучают процессы переноса энергии, импульса, заряда и вещества в разл-х физических сис-мах (газах, плазме, жидкостях, твёрдых телах) и влияние на них внешних полей. Процесс самопроизвольного перехода сис-мы в равновесное состояние называется релаксацией, а время этого процесса - временем релаксации. До истечения времени релаксации состояние сис-мы остается неравновесным, а сам процесс релаксации является неравновесным. Молекулы газа, находясь в состоянии хаотического движ-я, непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы проходят некоторый путь l, который называется длиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна, но так как мы имеем дело с огромным числом молекул и они находятся в беспорядочном движ-и, то можно говорить о средней длине свободного пробега молекул Эффективное сечение- величина, характеризующая вероятность перехода сис-мы 2 сталкивающихся частиц в результате их рассеяния (упругого или неупругого) в определённое конечное состояние. Э.с. равно отношению числа dN таких переходов в единицу времени к плотности nv потока рассеиваемых частиц, падающих на мишень.Э.с. имеет размерность площади; обычно оно измеряется в см2.В часто встречающемся случае упругого рассеяния пучка частиц, движущихся с одинаковой скоростью, на некотором центре, используется дифференциальное эффективное поперечное сечение (dσ/dΩ)(определённый телесный угол dΩ).Интегрирование по полному телесному углу даёт полное поперечное сечение, для рассеяния на любые углы: При наличии неупругих взаимодействий полное сечение складывается из сечения для упругих и неупругих рассеяний. Для каждого типа неупругих взаимодействий может быть введено отдельное эффективное сечение.

Общий механизм явлений переносов. Диффузия и теплопроводность в газах, жидкостях и твердых телах. Интегральные уравнения диффузии, теплопроводности и вязкости

В газе, находящемся в неравновесном состоянии, возникают необратимые процессы, называемые явлениями переноса.В ходе этих процессов происходит пространственный перенос вещества (диффузия), энергии (теплопроводность), импульса направленного движ-я (вязкое трение). Если течение процесса не изменяется со временем, то такой процесс называется стационарным.Диффузия, теплопроводность, вязкость являются необратимыми процессами, возникающими самопроизвольно вследствие теплового движ-я при отклонении вещества (газа) от равновесного состояния.Диффузия-взаимопроникновение вещества в разл-х смесях, сопровождающееся направленным переносом массы вещества из мест с высокой плотностью в места с меньшей плотностью. Перенос массы вещества подчиняется закону Фика: где D – коэф-т диффузии. Масса М вещества, перенесенная в результате стационарной диффузии через площадь S за время t: .Согласно кинетической теории газов, Наиболее быстро процесс протекает в газе, если он неоднороден по составу. Значительно медленнее протекают подобные процессы в жидкостях. Взаимопроникновение двух разнородных жидкостей друг в друга, растворение твердых веществ в жидкостях (например, сахара в воде) – примеры диффузионных процессов в жидкостях. Наиболее медленно процесс диффузии протекает в твердых телах. Однако, опыты показывают, что при контакте хорошо очищенных поверхностей двух металлов через длительное время в каждом из них обнаруживается атомы другого металла.Теплопроводность.Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул темп-ра выравнивается. Процесс передачи энергии в форме тепла подчиняется закону Фурье. 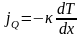,где  - коэф-т теплопроводности.Количество тепла, переносимое в стационарном процессе теплопроводности через площадь S за время t .Для идеального газа где c_v – удельная теплоемкость газа при постоянном объеме,  - плотность газа. Выразим от сюда коэ-т вязкости .