6.Изотермы Эндрюса и Ван-Дер-Ваальса. Метастабильные сотояния. Физический смысл критического сотояния

Д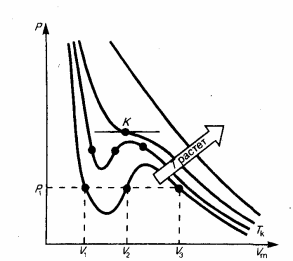 ля исследования поведения реального газа рас-м изотермы Ван-дер-Ваальса — кривые зависимости р от V_m при заданных Т, определяемые уравнением Ван-дер-Ваальса для моля газа.При высоких темп-рах (T > T_к) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кри­вой. При некоторой температуре T_к на изотерме имеется лишь одна точка перегиба К.Эта изотерма называется критической(T_к ); точка перегиба К называется критической точкой.Соответствующие этой точке объем V_к, и давление р_к называются также критическими. Состояние с критическими парамет­рами (p_к, V_к, T_к) называется критическим состоянием. При низких темп-рах (Т < T_к ) изотермы имеют волнообразный участок.Для пояснения характера изотерм преобразуем уравнение Ван-дер-Ваальса к виду Уравнение при заданных р и Т является уравнением третьей степени от­носительно V_m.Первому случаю соответствуют изотермы при низких темп-рах (три значения объема газа V₁, V₂ и V₃ отвечают одному значению давления р₁), второму случаю -изотермы при высоких темп-рах.Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным. Данные выводы, следующие из анализа уравнения Ван-дер-Ваальса, были под­тверждены опытами ирландского ученого Т. Эндрюса.Отличие экспериментальных (Эндрюс) и те­оретических (Ван-дер-Ваальс) изотерм заключается в том, что превращению газа в жидкость в первом случае соответствуют горизонтальные участки, а во вто­ром — волнообразные. Для нахождения критических параметров подставим их значения в уравнение и запишем . Поскольку в критической точке все три корня совпадают и равны V_к уравнение приводится к виду Tax как эти уравнения тождественны, то в них должны быть равны и коэф-ты при неизвестных соответствующих степеней. Поэтому можно записать

Решая полученные уравнения, найдем С равнивая изотерму Ван-дер-Ваальса с изотермой Эндрюса (верхняя кривая на рис2), видим, что последняя имеет прямолинейный участок 2—6, соответствующий двухфазным состояниям вещества. Правда, при некоторых условиях могут быть ре­ализованы состояния, изображаемые участками ван-дер-ваальсовой изотермы 5—6 и 2—3. Эти неустойчивые состояния называются метастабильными

7.Фазы и компоненты. Условие равновесия фаз. Фазовые переходы первого и второго уровня

Очевидно, что для равновесия фаз, как и для равновесия любых частей сис-мы, должны быть равными их темп-ры: T1 = T2 .Кроме того, условие непожвижности границы между фазами требует равенства их давлений: P1 = P2 .Однако этого недостаточно для равновесия фаз.Равновесие 2 фаз достигается при = их химических потенциалов.В веществе, состоящем из k компонент, одновременно могут сущ-ть не более чем k + 2 равновесные фазы. Переход между жидким и газообразным состояниями был назван фазовым переходом первого рода. Переход жидкость-твердое тело также является фазовым переходом первого рода.При рассмотрении гелия нам встретился другой тип фазового перехода - λ-переход(фазовый переход второго рода).Особенностью фазовых переходов первого рода является скачкообразное измен-е удельной внутренней энергии и связанных с ней величин в точке перехода и наличие скрытой теплоты перехода.Темп-ра, при которой осуществляется фазовый переход, называется точкой Кюри. Поскольку переход реализуется сразу во всем объеме, не существует пространственного разделения фаз и их нахождения в равновесии друг с другом.Фазовый переход второго рода не сопровождается выделением или поглощением теплоты фазового превращения.Объем при переходе не меняется, но теплоемкость в связи с измен-ем симметрии сис-мы меняется. Это означает, что производная dСv/dТ меняется скачком, как и температурный коэф-т объемного расширения, хотя сам объем постоянен.