Единицы энтропии

Полученная Шенноном формула позволила вывести единицы измерения количества информации. Для этого приравняем выражение для энтропии системы к единице:

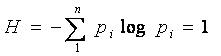
Какие переменные входят в это выражение:

1. Число возможных состояний системы n

2. Основание логарифма a

3. Распределение вероятностей pi

Для решения уравнения необходимо задаться из каких-либо соображений двумя переменными и вычислить третью.

БИТ

Рассмотрим физическую систему с двумя равновероятными состояниями. Количество информации равное единице может быть получено, если в формуле Шеннона и взять логарифм по основанию 2. Пусть n=2 и , тогда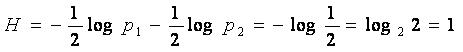 

Следовательно, в данном случае единицей энтропии служит энтропия системы с двумя равновероятными состояниями, вычисленная с помощью логарифма с основанием два. Полученная единица количества информации, представляющая собой выбор из двух равновероятных событий, получила название двоичной единицы, или бита. Название bit образовано из двух начальных и последней букв английского выражения binary unit, что значит двоичная единица

Другими словами, если мы приняли, что информация – это устраненная неопределенность, тогда в случае неопределенности физической системы с двумя равновероятными состояниями выбор будет производиться между двумя взаимоисключающими друг друга равновероятными сообщениями, например, между двумя качественными признаками: положительным и отрицательным импульсами, импульсом и паузой и т.п. Количество информации, переданное в этом простейшем случае, принято за единицу количества информации - бит. Бит является единицей количества информации и представляет собой информацию, содержащуюся в одном дискретном сообщении источника равновероятных сообщений с объемом алфавита равного двум.

ДИТ

Возьмем основание логарифма равным 10-ти и рассмотрим физическую систему с числом n равновероятных состояний. Определим, чему должна быть равна переменная n, чтобы количество информации в формуле Шеннона было равно единице, когда взят логарифм по основанию 10:

Пусть а=10 и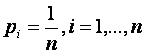 

Тогда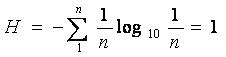 

Поскольку отсюда следует, что , тогда число состояний n=10. Итак, дит – это энтропия системы с десятью равновероятными состояниями, вычисленная с помощью логарифма с основанием десять.

Можно заметить, что основание логарифма равно числу состояний. Это – важное замечание! Перейдем теперь к рассмотрению виртуальной системы с количеством состояний, равным натуральной единице е. Дит - единица количества информации, содержащейся в одном дискретном сообщении источника равновероятных сообщений с объемом алфавита, равного десяти.

НИТ

Если взять физическую систему с е состояниями, получим натуральную единицу количества информации, называемую нитом, при этом основание логарифма в формуле Шеннона равно е=2,7.

Взаимосвязь между единицами количества информации:

 

Свойства энтропии

Свойство 1

Неопределенность физической системы равна нулю: H = H(p1, p2, …, pn) = 0, если одно из чисел p1, p2, …, pn равно 1, а остальные равны нулю.

Доказательсто:

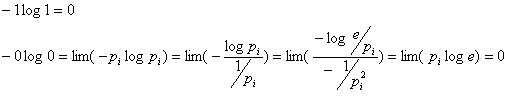
Свойство 2

Энтропия максимальна, когда все состояния источника равновероятны.

Доказательство:

Введем ограничение на :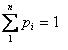 

Ищем локальный экстремум. Для этого рассмотрим функционал  ,где  по Лагранжу,

а   - из условия ограничения.

Берем первые частные производные по  ::

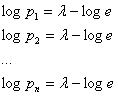
Поскольку правые части всех выражений одинаковые, можно сделать вывод о равновероятных состояниях физической системы, то есть: ,

Тогда:

Получили выражение для максимальной энтропии, соответствующее формуле Хартли.

Свойство 3

Всякое изменение вероятностей p1, p2, …, pn в сторону их выравнивания увеличивает энтропию H(p1, p2, …, pn).

Доказательство:

,

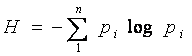 и 

Пусть  > , тогда  ,

+ +…+  

Нам нужно доказать, что 

 

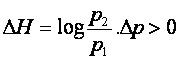 и    , так как  , что и требовалось доказать.

 

Свойство 4

Математическое ожидание вероятности есть энтропия (Без доказательства)

Код Хаффмана

Оптимальное кодирование информации. Важной задачей современной информатики является кодирование информации наиболее коротким способом. На сегодняшний день разработаны универсальные способы кодирования информации, например, алгоритм Хаффмана (1952 год), который является простым, быстрым и оптимальным. В основу алгоритма Хаффмана положена идея: кодировать более коротко те символы, которые встречаются чаще, а те, которые встречаются реже кодировать длиннее. При этом возникает проблема: как понять, где кончился код одного символа и начался код другого? Эту проблему можно решать двумя способами:

1. Закодированная последовательность имеет вид {длина кода, код} {длина кода, код} … {длина кода, код}

2. Строится так называемый префиксный код: в нем не требуется указывать длину кода, но коды получаются несколько длиннее. Код Хаффмана является префиксным.

• Определение: Префиксный код – это код, в котором код одного символа не может быть началом кода другого символа.

Задание: Построить код Хаффмана для алфавита, состоящего из 5-ти символов a, b, c, d, e с частотами (вероятностями появления в тексте) 0,37 (a); 0,22 (b); 0,16 (c); 0,14 (d); 0,11 (e)

Решение: Объединим символы d, e (символы с наименьшими частотами), тогда частота символа de равна 0,14 (d) + 0,11 (e) = 0,25 (de) , получаем новые частоты 0,37 (a); 0,22 (b); 0,16 (c); 0,25 (de) Объединим символы a, de (символы с наибольшими частотами), тогда частота символа ade равна 0,37 (a) + 0,25 (de) = 0,62 (ade), получаем новые частоты 0,62 (ade); 0,22 (b); 0,16 (c) Объединим символы b, c (символы с наименьшими частотами) , тогда частота символа bc равна 0,22 (b) + 0,16 (c) = 0,38 (bc), получаем новые частоты 0,62 (ade); 0,38 (bc) Сопоставим ade код 0 , bc - код 1 (Символу с большей частотой - более короткий код) Расщепим символ ade на символы a и de с кодами 00 и 01 Расщепим символ bc на символы b и с с кодами 10 и 11 Расщепим символ de на символы d и e с кодами 010 и 011

Ответ: Коды исходного алфавита a, b, c, d, e следующие: 00 (a); 10 (b); 11 (c); 010 (d); 011 (e) Полученный код – префиксный, код каждого символа не является началом кода другого символа. Однако, определить, что построенный код для конкретной последовательности – минимальный, нельзя.

Это не означает, что ни для какого объекта минимальную последовательность построить нельзя. А означает, что часто невозможно доказать минимальность построенной последовательности.