Понятие «информация»

Человек изучает информационные явления и процессы, происходящие в человеческом обществе. В научном плане информатика занимается изучением свойств информации и закономерностями ее движения, переработки и хранения, В практическом плане информатика изучает способы сбора, переработки, хранения и передачи информации с помощью технических устройств, важнейшим из которых является компьютер. Все эти процессы, связанные с операциями над информацией, называются информационными процессами. Что же означает слово «информация»? Человек стал употреблять это слово давно, впервые оно встречается еще у древних греков. В переводе с латинского оно означает сообщение, получение сведений и первоначально относилось к обмену сведениями между людьми.

Информация в самом общем смысле - это понятие, описывающее обмен сведениями между людьми, человеком и автоматом, между автоматами, обмен сигналами в животном и растительном мире, передачу признаков от клетки к клетке, от организма к организму. Из-за многозначности понятия «информация» дать его четкое определение очень трудно, можно лишь попытаться выразить его через другие известные понятия. Можно выделить, по крайней мере, четыре различных подхода к определению понятия «информация».

• В первом, «обыденном», слово «информация» применяется как синоним слов: сведения, знания, сообщения.

• Во втором, «кибернетическом» (кибер – рулевой, кибернетика – наука об управлении), слово «информация» используется для характеристики управляющего сигнала, передаваемого по линии связи.

• В третьем, «философском», слово «информация» связано с понятиями взаимодействие, отражение, познание.

• B четвертом, «вероятностном», слово «информация» вводится как мера уменьшения неопределенности и позволяет количественно измерять информацию.

Для измерения количества информации нужна единица измерения

За единицу количества информации приняли такое количество информации, при котором неопределенность уменьшается в 2 раза. Такая единица названа «бит».

Например, при бросании монеты существует два равновероятных исхода (события): «орел» или «решка». Монета упала, событие произошло, количество информации равно 1 бит.

В компьютере информация представляется в виде последовательности из нулей и единиц (двоичное кодирование). Цифры 0 и 1 можно рассматривать как два равновероятных события, а один двоичный разряд содержит количество информации, равное 1 биту. Два двоичных разряда несут соответственно 2 бита информации.

Информационный объем сообщения - количество двоичных символов, используемое для кодирования этого сообщения.

Каждому символу в компьютере соответствует последовательность из 8 нулей и единиц, называемая байтом:

1 байт = 8 битам

Например, слово МИР в компьютере выглядит следующим образом: {М}11101101 {И}11101001 {Р}11110010.

Последовательностью нулей и единиц можно закодировать и графическую информацию, разбив изображение на точки. Если только черные и белые точки, то каждую можно закодировать 1 битом.

Используются и более крупные единицы измерения количества информации:

• 1 Кбит (килобит) = 2¹⁰ бит = 1024 бит

• 1 Мбит (мегабит) = 2¹⁰ Кбит = 1024 Кбит

• 1 Гбит (гигабит) = 2¹⁰ Мбит = 1024 Мбит

• 1 Кбайт (килобайт) = 2¹⁰ байт = 1024 байт

• 1 Мбайт (мегабайт) = 2¹⁰ Кбайт = 1024 Кбайт

• 1 Гбайт (гигабайт) = 2¹⁰ Мбайт = 1024 Мбайт

• 1 Тбайт (терабайт) = 2¹⁰ Гбайт = 1024 Гбайт

1. Формула Хартли

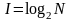
N – количество равновероятных вариантов выбора

I – количество бит информации, которое несёт каждый из вариантов

2. Ф ормула Шеннона

J_i – количество информации, которое несёт i-й вариант из N неравновероятных вариантов выбора

Р_i – вероятность i-го варианта

3. О бобщенная формула Шеннона

H – среднее количество информации, содержащейся в тексте из N символов n-буквенного алфавита

Средние частоты и количество информации букв русского алфавита

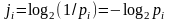
Буквы	А	Б	В	Г	Д	Е, Ё	Ж	З
pi	0.062	0.014	0.038	0.013	0.025	0.072	0.007	0.016
ji	4.012	6.158	4.718	6.265	5.322	3.796	7.158	5.966

Буквы	И	Й	К	Л	М	Н	О	П
pi	0.062	0.010	0.028	0.035	0.026	0.053	0.090	0.023
ji	4.012	6.644	5.158	4.837	5.265	4.238	3.474	5.442

Буквы	Р	С	Т	У	Ф	Х	Ц	Ч
pi	0.040	0.045	0.053	0.021	0.002	0.009	0.004	0.012
ji	4.644	4.474	4.238	5.574	8.966	6.796	7.966	6.381

Буквы	Ш	Щ	Ъ, Ь	Ы	Э	Ю	Я	__
pi	0.006	0.003	0.014	0.016	0.003	0.006	0.018	0.175
ji	7.381	8.381	6.158	5.966	8.381	7.381	5.796	2.515

Средняя информационная ёмкость символа алфавита

4. Закон аддитивности информации

Количество информации H(x1 , x2), необходимое для установления пары(x1 , x2), равно сумме количеств информации H(x1) и H(x2), необходимых для независимого установления элементов x1 , x2 H(x1 , x2) = H(x1) + H(x2)

Задание 1: Используя закон аддитивности и формулу Хартли, подсчитать, какое количество информации несет достоверный прогноз погоды.

Решение: Предположим, что прогноз погоды на следующий день заключается в предсказании дневной температуры (обычно делается выбор из 16 возможных для данного сезона значений) и одного из 4-x значений облачности (солнечно, переменная облачность, пасмурно, дождь). Тогда, H(x1 , x2) = H(x1) + H(x2) = log₂ 16 + log₂ 4 = = 4 + 2 = 6 бит Закон аддитивности информации справедлив и при алфавитном подходе к измерению информации. Для хранения двух произвольных символов одного и того же алфавита мощности N потребуется не менее

log ₂ N + log ₂ N = 2 log ₂ N

То есть количество информации, содержащееся в сообщении, состоящем из m символов одного и того же алфавита, равно m log 2 N

Задание 2: Вычислить какой объем памяти компьютера потребуется для хранения одной страницы текста на английском языке, содержащей 2400 символов.

Решение: Мощность английского алфавита, включая разделительные знаки, N = 32. Тогда для хранения такой страницы текста в компьютере понадобится 2400 log₂ 32 бит = 2400 • 5 =12000 бит = 1500 байт

Задание 3: В течение 5 секунд было передано сообщение, объем которого составил 375 байт. Каков размер алфавита, с помощью которого записано сообщение, если скорость передачи составила 200 символов в секунду?

Решение: Скорость передачи равна 375 байт. 5 = 75 байт / с 75 байт / с соответствуют 200 символам / с. В одном символе содержится 75 байт ? 200 = 0,375 байт = 3 бита, то есть log 2 N = 3 бита , тогда N = 23 = 8 символов