Шпоры по матану 2011-2012 / матан шпоры 6

Непрерывность функции на отрезке.

ОПР. Функция непрерывна на отрезке, если она непрерывна в каждой точке этого отрезка.

ОПР. Функция 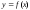ограничена на отрезке [a;b], если .

1- я теорема Вейерштрасса

Всякая непрерывная функция на отрезке ограничена на этом отрезке.

ДОК. Предположим противное: функция на отрезке [a;b] неограниченна  . Последовательность ограничена по построению, поэтому по теореме у нее есть предельная точка . Поскольку функция непрерывна в точке c , она ограничена в окрестности этой точки ( теорема об ограниченности функции, имеющей предел),

т.е. . Тогда в окрестности может находиться не более конечного числа членов последовательности , что противоречит тому, что c – предельная точка последовательности .

Доказано, что множество значений функции ограничено. Тогда по теореме о точной верхней и нижней грани существует и.

ОПР. Если , то А называется наименьшим значением функции на отрезке [a;b].

Обозначение .

ОПР. Если , то В называется наибольшим значением функции на отрезке [a;b].

Обозначение .

2 – я теорема Вейерштрасса

Непрерывная функция на отрезке принимает наименьшее и наибольшее значения.

ДОК. (1) Пусть . Тогда, по определению точной нижней грани, . Последовательность ограничена, поэтому у нее есть предельная точка c₁. Тогда у нее есть подпоследовательность , для которой и по теореме о промежуточной последовательности .

Поскольку функция непрерывна в точке , , т.е..

(2) Пусть . Тогда, по определению точной верхней грани, . Последовательность ограничена, поэтому у нее есть предельная точка c₂. Тогда у нее есть подпоследовательность , для которой , и по теореме о промежуточной последовательности . Поскольку функция непрерывна в точке , , т.е..

Теорема о нуле непрерывной функции

Пусть - непрерывная функция на отрезке , причем . Тогда существует точка .

ДОК. Разобьем отрезок пополам. Если 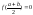, то теорема доказана. Если , то выберем тот из отрезков разбиения, для которого значения функции на концах отрезка имеют разные знаки. Обозначим этот отрезок через . Повторим процесс деления : выберем тот из отрезков разбиения отрезка , для которого значения функции на концах отрезка имеют разные знаки. Обозначим этот отрезок и т.д. Построенная последовательность вложенных отрезков – стягивающаяся. По теореме о системе стягивающихся отрезков существует точка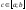, принадлежащая каждому из отрезков . Если , то из непрерывности функции следует, что сохраняет знак в некоторой окрестности , что противоречит способу построения последовательности отрезков , т.е. .