Шпоры по матану 2011-2012 / матан шпоры 4

Предел функции.

Рассмотрим функцию и точку такую, что . В частности, точка может быть внутренней точкой для E : .

ОПР.(КОШИ) Число А называется пределом функции в точке , обозначение , если .

ОПР.(ГЕЙНЕ) Число А называется пределом функции в точке , обозначение , если

Множество V на числовой оси называется открытым, если . Любое открытое множество V(a), содержащее точку a , называют окрестностью точки a .

ОПР.(ТОПОЛОГИЧЕСКОЕ) Число А называется пределом функции в точке , обозначение , если

Если А – предел по Коши => А – предел по Гейне

ДОК. (1) Пусть по Коши : .

Пусть произвольная последовательность, для которой .Тогда , т.е..

(2) Пусть по Гейне.

Предположим, что число А не является пределом функции по Коши. Тогда .

Построенная последовательность сходящаяся и . Тогда . Полученное противоречие доказывает, что число А является пределом функции по Коши.

ОПР. Функция называется ограниченной в окрестности , если существует число М, для которого

.

Ограниченность функции в окрестности точки ДОК. Из определения предела, следует для существует такая, что

.

Теорема о единственности предела функции Если функция имеет предел в точке , то он только один.

ДОК. Предположим противное: Числа А и В являются пределами функции, причем . Выберем , тогда существует окрестность , для которой

.

Тогда , что противоречит выбору числа .

Теорема о переходе к пределу в неравенстве

Пусть функции и имеют пределы

А и В в точке и , для всех .

Тогда .

ДОК. Предположим противное: . Выберем . Тогда существует окрестность , для которой

,

что противоречит условию теоремы.

ОПР. Функция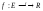 называется бесконечно малой функцией в точке a , если .

ОПР. Функция называется бесконечно большой функцией в точке a , если