Шпоры по матану 2011-2012 / матан шпоры 1

Множества.

Объединение множеств.

Пересечение множеств

Разность множеств.

Симметрическая разность.

Отрицание множеств. .

ПРИМЕР 1. А – множество студентов, сдавших физику и математику на оценку 4 или 5.

В – множество студентов с рыжими волосами.

С – множество студентов, занимающихся спортом.

Какие студенты входят в множество ?

Ответ : это либо не рыжие хорошисты, не занимающиеся спортом,

либо рыжие троечники не занимающиеся спортом.

Алгебра множеств (примеры).

1) .

2)

3)

Аксиомы вещественных чисел.

1. Аксиомы сложения. В множестве вещественных чисел определена

операция сложения, т.е.определено вещественное число ,

причем эта операция удовлетворяет условиям:

1.1 существует нуль, т. элемент , для которого .

1.2 существует «противоположный» элемент :.

1.3 «правило расстановки скобок»: .

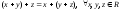1.4 коммутативность : .

2. Акс. Умнож.. Во множестве вещественных чисел определена операция умножения,

определено вещественное число , эта операция удовлетворяет условиям :

2.1 существует единица, т. элемент , для которого .

2.2 для каждого существует «обратный» элемент ,

для которого .

2.3 «правило расстановки скобок» : .

2.4 коммутативность :

3. Аксиомы сложения и умножения.

3.1 правило раскрытия скобок :

4. Аксиомы порядка.

Во множестве действительных чисел определено отношение порядка ,

т.е. для каждой пары справедливо одно из высказываний : или ,

при этом это отношение удовлетворяет условиям :

4.1

4.2 Если и , то .

4.3 Если и , то .

4.4 Если , то .

4.5 Если и , то

5. Аксиома полноты.

5.1 Пусть X,Y и Z подмножества R такие, что и , причем

и справедливо высказывание . Тогда ,

для которого для любых

Множество , содержащее более двух элементов, с введенными операциями сложения

и умножения, удовлетворяющими аксиомам 1-5 ,называется множеством вещественных

чисел, а его элементы – вещественными (или действительными) числами.

СЛЕДСТВИЯ из аксиом.

Сл1. Единственность нуля.

Док. Если нуля два, , то .

Сл2. .

Док. .

Сл3.

Док. , т.е..

Сл4.

Док.

, т.е. .

Понятия и

ОПР. Числовое множество Х называют ограниченным

сверху, если найдется число М, для которого

.

ОПР. Числовое множество Х называют ограниченным

снизу, если найдется число m, для которого

.

ОПР. Числовое множество Х называют ограниченным ,

если найдутся числа m и М, для которых

.

Наименьшее из чисел М, ограничивающих сверху

множество Х, называют точной верхней гранью этого

множества. Аналогично, наибольшее из чисел m ,

ограничивающих множество Х снизу, называют точной

нижней гранью множества Х. Точнее об этом в

ОПР. Число называют точной верхней гранью

множества Х,, если выполнены два условия :

1) , 2) .

ОПР. Число называют точной нижней гранью множества Х,

, если выполнены два условия

1) ,2) .

Точные верхняя и нижняя грани множества Х могут не принадлежать множествуХ.

ПРИМЕР 1. Множество Х является множеством значений последовательности . Найти и .

РЕШЕНИЕ. Докажем, что . Действительно, . Для любого . Решаем последнее неравенство относительно n : . Заметим, что . Поскольку

последовательность возрастающая, то

, т.е.и .

ТЕОРЕМА 1. Любое непустое, ограниченное сверху множество , имеет .

ДОК. Пусть У – множество верхних граней множества Х: . По аксиоме о полноте множества вещественных чисел (аксиома 5), найдется число , для которого

.

Таким образом, и является в нем наименьшим элементом, т.е. .

Замечание. Множество Х имеет только одну точную верхнюю грань.

ДОК. Пусть и - две такие грани и . Тогда по определению для найдется , что противоречит условию .Аналогично доказывается

ТЕОРЕМА 2. Любое непустое, ограниченное снизу множество , имеет и единственное .

Система вложенных отрезков.

ОПР. Система отрезков называется системой вложенных отрезков, если .

ТЕОРЕМА 5. Любая система вложенных отрезков имеет общую точку.

ДОК. Рассмотрим множества и . Множества А и В ограничены и . Тогда по аксиоме полноты существует , для которого

., т.е .

ОПР. Система вложенных отрезков называется стягивающейся, если .

ТЕОРЕМА 6. Система стягивающихся отрезков имеет единственную общую точку.

ДОК. Пусть с₁ и с₂ две такие точки и

.

Тогда ,т.е..

Последнее противоречит условию стягивания.

ТЕОРЕМА 7 . Множество всех точек отрезка несчетно.

ДОК. Предположим обратное : . Разобьем отрезок и выберем тот из отрезков, который не содержит х₁. Далее полученный отрезок разобьем на три части и выберем тот, который не содержит х₂ и т.д. Полученная совокупность вложенных отрезков стягивающаяся. По теореме 1 существует число , не совпадающее ни с одним из x_n . Полученное противоречие доказывает , что множество [0;1] несчетно. Множества равномощные с [0;1] называются множествами мощности континуума.