Шпоры по матану 2011-2012 / матан шпоры 5

Первый замечательный предел

.

ДОК. (см. рис) Для всех справедливы неравенства : ( - длина дуги АВ₁ , а - длина дуги катета АВ) и .

Функция б.м.ф. в точке и поэтому, на основании теоремы о промежуточной функции, 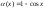также б.м.ф.Тогда из теоремы о связи .

Площадь  ОАВ , площадь сектора АОВ₁, площадь ОА₁В_1.Справедливо неравенство : площадь  ОАВ< площадь сектора ОАВ< площадь ОА₁В₁

.

По доказанному 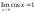, поэтому на основании теорем о промежуточной функции и арифметической теореме о пределах .

ПРИМЕР. Вычислить .

РЕШЕНИЕ. .

Второй замечательный предел

.

ДОК. (1) Пусть произвольная последовательность, ,для которой .

Тогда и для каждого n найдутся натуральные числа или . Справедливо неравенство

.

Последовательности и сходятся к числу e , поэтому на основании теоремы о промежуточной последовательности по Гейне, а значит и по Коши.

(2) Пусть - произвольная последовательность, , для которой .Обозначим . Тогда .

Обозначим .Тогда и . Из доказанного в (1) следует, что .

СЛЕДСТВИЯ (1) .

ДОК.

(2) .

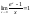ДОК. Замена .

.

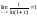Эквивалентные бесконечно малые и называются эквивалентными, если .

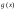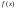
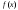
Обозначение  . Отношение эквивалентности транзитивно:  , , то и симметрично:    .

ТАБЛИЦА ЭКВИВАЛЕНТНЫХ БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ в точке x = 0 .

(1)  (2)   , (3)  , 4)  , (5)  (6)  , (7)  (8)  ,(9)  , (10) 

ДОК. Формулы (1)- (3), (6), (8) уже обсуждались, (7) и (9) получаются из них переходом к основанию e , сделав замену и , (5) – аналогично, (10)   .

Теорема о замене бесконечно малой на эквивалентную

Если бесконечно малые функции  ,   в точке , и существует , то .

ДОК. .

ТЕОРЕМА 2. (о связи эквивалентных бесконечно малых)

Если две бесконечно малые функци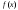и и эквивалентны в точке , то. Если бесконечно малые функции и связаны соотношением

,то они эквивалентны.

ДОК.(1)

(2).

Непрерывность функции в точке. Арифметические теоремы о непрерывных функциях. Непрерывность сложной функции.

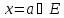ОПР. Функция непрерывна в точке , если .

ОПР. (эквивалентное).Функция непрерывна в точке 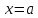, если ее приращение - БМФ в точке .

(здесь )

ДОК. Эквивалентность определений следует из теоремы о связи функции, имеющей предел, и бесконечно малой функции.

Т1. (арифметическая теорема о непрерывных функциях)

Пусть функции и 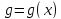непрерывны в точке . Тогда сумма , произведение , и частное , (- непрерывные функции в точке .

ДОК. Следует из арифметической теоремы о пределах.

ОПР. Пусть заданы две функции и , точка .. Тогда функция , определенная по правилу , называется композицией функций и или сложной функцией.

Т2. (о непрерывности сложной функции)

Если функция непрерывна в точке , функция непрерывна в точке , то сложная функция непрерывна в точке .

ДОК. Из условия теоремы

и

Тогда и .