Шпоры по матану 2011-2012 / матан шпоры 7

Теорема о существовании и непрерывности обратной функции

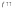Если (или ) непрерывная функция на [a;b], то существует и единственная обратная к ней функция , определенная на отрезке и непрерывная, строго возрастающая ( или убывающая ) на этом отрезке.

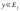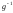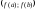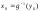
ДОК. Пусть и непрерывна на [a;b]. Тогда и для любого существует и единственное значение , для которого . Действительно, если таких значений два и , например , то . Положим . Тогда на , т.е. обратная к функция. Докажем ее непрерывность на . Пусть произвольная точка интервала и . Тогда для любого

существует такое, что выполняется неравенство . Строгое возрастание функции следует из неравенств : .

Непрерывность функции в граничных точках и следует из теоремы 1 : ,

Понятие производной функции

ОПР. . Производной функции в точке , называют число .

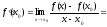
ПРИМЕР 1 Вычислить производную функции в произвольной точке x .

РЕШЕНИЕ. .

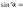
МЕХАНИЧЕСКИЙ смысл производной.

- путь, пройденный материальной точкой к моменту времени t , - расстояние, пройденное точкой за время , - средняя скорость движения,

- скорость в момент времени t .

ГЕОМЕТРИЧЕСКИЙ смысл производной.

Точки и на графике функции соединены прямой L_сек – секущей, -

угловой коэффициент прямой L_сек .

При прямая L_сек поворачивается вокруг точки А, занимая предельное положение - - касательной к графику функции в точке А.

- угловой коэффициент ( тангенс угла наклона ) касательной. Производная функции в точке x равна тангенсу угла наклона касательной, проведенной к графику функции в точке с абсциссой x .

Теорема о непрерывности функций имеющих производные

Если функция имеет производную в точке , то она непрерывна в этой точке.

ДОК. .

Тогда , где - бесконечно малая функция в точке ., т.е. .

ПРИМЕР 2 . Функция непрерывна в точке , но не имеет производной в этой точке.

РЕШЕНИЕ. - бесконечно малая функция в точке , т.е.функция непрерывна в точке .Функция 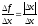не имеет предела в точке , поскольку , и пределы справа и слева не совпадают.

Арифметическая теорема о производных

Если функции и имеют производную в точке , то

(1)

(2)

(3) , при .

ДОК. (2)

,

т.к. функция непрерывна в точке (теорема 4).

(3) , поскольку при функция

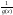непрерывна в точке (теорема 4).