Шпоры по матану 2011-2012 / матан шпоры 2

Последовательности, предел последовательности.

ОПР. Последовательностью называют числовую функцию, заданную на множестве N натуральных чисел.

.

Последовательность может задаваться явно, например,

(1) (2) (3) (4)

и рекуррентно, например, (5) (ариф. прогр.)

(6) (геом. прогр.) (7) .

ОПР.Последовательность ограничена (сверху, снизу), если этим свойством обладает множество ее значений.

ОПР. Последовательность монотонно возрастает (убывает), если () для любого n. Если неравенства строгие, говорят о строгом возрастании (убывании) последовательности.

В примерах (1) монотонно возрастающая, ограниченная последовательность. (2) ограниченная, не монотонная последовательность. (3) монотонно возрастающая, неограниченная последовательность (4) неограниченная, не монотонная последовательность.(5) неограниченная, монотонно убывающая при d<0, монотонно возрастающая при d>0.(6) ограниченная при , неограниченная при ,монотонная при , не монотонная при .

ОПР. Окрестностью точки х₀ радиуса >0 называют множество

ОПР. Множество называют выколотой окрестностью точки х₀.

ОПР. Число В называют предельной точкой (частичным пределом) последовательности , если окрестность

содержит бесконечное число членов последовательности .

В примерах (1) число В=3 является единственной предельной точкой последовательности. (2) числа являются предельными точками последовательности. (3), (4), (5) предельных точек не имеют (6) число В=0 предельная точка при , при предельных точек нет.

ОПР. Число А называется пределом , если А – предельная точка и вне любой окрестности содержится не более конечного числа членов последовательности , или

.

Если последовательность имеет предел, то она называется сходящейся.

В примерах (1) имеет предел А=3.(2), (3), (4), (5) – предела не имеют.(6) имеет предел А=0 при , не имеет предела при .

ТЕОРЕМА1. Всякая ограниченная последовательность имеет хотя бы одну предельную точку.

ДОК. Из ограниченности последовательности следует существование отрезка [c₁;b₁], для которого . Разделим отрезок пополам и выберем ту половину , которая содержит бесконечное число . Если обе половины обладают этим свойством, то выбираем любую. Делим отрезок пополам и выбираем ту половину , которая содержит бесконечное число . Продолжая процесс деления, построим систему стягивающихся , вложенных отрезков .

По теореме существует число В , принадлежащее каждому отрезку . Тогда окрестность содержит отрезок с достаточно большим номером n_ , но тогда , по построению последовательности в окрестности содержится бесконечное число членов последовательности .

ОПР. Последовательность называется подпоследовательностью , если .

Всякая предельная точка подпоследовательности является предельной точкой последовательности .

ТЕОРЕМА 2. Если последовательность имеет предельную точку В, то существует сходящаяся ее подпоследовательность, имеющая В своим пределом.

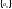ДОК. Выберем в каждом отрезке , описанном в ТЕОРЕМЕ 1, член последовательности . Тогда подпоследовательность , , имеет по построению число В своим пределом.

В примере (2) подпоследовательность , имеет предел В₁=1, подпоследовательность , имеет предел В₂=0,5, подпоследовательность , имеет предел

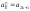В₃= - 0,5, подпоследовательность , имеет предел В₄= - 1, (4) подпоследовательность , имеет предел В₁=1, подпоследовательность , имеет предел В₂= - 1.

ТЕОРЕМА 3. Если последовательность имеет предел равный А, то любая ее подпоследовательность сходящаяся, причем А является ее пределом.

ДОК. (самостоятельно)

ТЕОРЕМА 4.Всякая сходящаяся последовательность ограничена.

ДОК. Пусть и произвольно мало. Тогда, по определению предела, множество E_a значений членов последовательности с номерами принадлежати поэтому является ограниченным. Если добавит к E_a конечное множество значений с номерами , то полученное множество также будет ограниченным.

Теорема о единственности предела последовательности

ДОК. Пусть таких пределов два : А₁ и А₂. Выберем . Тогда окрестности и не пересекаются и в каждой из них должны содержатся все члены последовательности , кроме конечного их числа, что невозможно.

Теорема о существовании предела монотонной ограниченной последовательности

ДОК. Заметим, что из ограниченности сверху и условия следует ограниченность . Тогда по теореме 1 у нее есть предельная точка А. Докажем, что А является пределом последовательности . Пусть произвольная окрестность точки А. Из того, что А предельная точка следует, что

,

т.е. вне окрестности содержится только конечное число членов последовательности.

ОПР. Пусть М_а – множество предельных точек последовательности . Предположим, что оно не пусто и ограничено. Тогда числа и называют верхним и нижним пределами последовательности .

ТЕОРЕМА 7. Если последовательность ограничена, то числа и являются предельными точками, т.е. принадлежат .ДОК. Построим подпоследовательность , предел которой равен . По определению , для существует : . Тогда подпоследовательность сходящаяся и ее предел, т.е. - предельная точка. Доказательство для аналогично.