Шпоры по матану 2011-2012 / матан шпоры 10

Производные и дифференциалы высших порядков. Вторая производная функции, заданной параметрически. .

ПРИМЕРЫ Доказать, что

(1) (2)

(3) (4)

(5)

ДОК. По индукции. (3) 1) при n = 1

2) предположение . Тогда .

ПРИМЕР. Найти вторую производную функции, заданной параметрически:, . .

ОПР. Дифференциалом второго порядка функции , называют дифференциал от первого дифференциала. В общем случае,

.

Так .

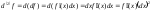В общем случае,

ПРИМЕР. Форма второго дифференциала не инвариантна.

ДОК. Если сложная функция получена композицией функций и , то и .

Если y – независимая переменная, то , т.е. форма второго дифференциала неизменна, если , в остальных случаях при переходе к сложной функции второй дифференциал изменяет свою форму.

ПРИМЕР. (Бином Ньютона)

Найдем коэффициенты многочлена .

Заметим, что -

коэффициенты бинома Ньютона. Тогда

.

Многочлен Тейлора, формула Тейлора с остаточным членом в форме Пеано.

ПРИМЕР. ( многочлен Тейлора)

Для каждой функции , имеющей n производных в точке , можно написать многочлен Тейлора: .

Заметим, что многочлен бинома Ньютона является многочленом Тейлора функции в точке . Разность называют остатком формулы Тейлора. Отметим некоторые свойства функции :

1) , поскольку .

2) , для т.к. .

3) .

ТЕОРЕМА 1 (формула Тейлора с остаточным членом в форме Пеано)

Если существует производная,то.

ДОК. Применим правило Лопиталя для вычисления предела:

.

П. 3 Формулы Тейлора для основных элементарных функций.()

(1) ,

(2) ,

(3) ,

(4) ,

(5) ,

(6) ,

(7)

ДОК. (2)

.

(3) , ,

,

(1)

(4) ,, ,.