
Шпоры по матану 2011-2012 / матан шпоры 8
.docxПроизводная обратной функции.
Пусть
 непрерывная, строго монотонная
(возрастающая или убывающая) функция
на отрезке [a;b]
и имеющая в точке
непрерывная, строго монотонная
(возрастающая или убывающая) функция
на отрезке [a;b]
и имеющая в точке
 производную
производную
 .
Тогда обратная функция
.
Тогда обратная функция
 имеет производную в точке
имеет производную в точке
 и
и
 .
.
ДОК.

=
 .
.
Производная сложной функции.
Пусть функция
 ,
определенная и непрерывная в окрестности
,
определенная и непрерывная в окрестности
 ,
имеет производную в точке
,
имеет производную в точке
 .
Функция
.
Функция
 определена и непрерывна в окрестности
определена и непрерывна в окрестности
 ,
где
,
где
 ,
и имеет производную в точке
,
и имеет производную в точке
 .
Тогда сложная функция
.
Тогда сложная функция
 имеет производную в точке
имеет производную в точке
 и
и
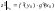 .
.
ДОК.

 ,
,
где
 и
и
 -
б.м.ф. Тогда
-
б.м.ф. Тогда

и
 ,
где
,
где
 б.м.ф. в точке
б.м.ф. в точке
 .
.
Тогда

 .
.
П.3 Таблица производных элементарных функций.
(1)
 (2)
(2)
 .
(3)
.
(3)

(4)
 (5)
(5)
 .
.
6)
 (7)
(7)

(8)
 (9)
(9)
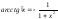
(10)
 (11)
(11)
 (12)
(12)

(13)

ДОК.
(10)



(11)
 .
.
(12)



 (13)
(13)

(1)

(2)
 =
= .
.
(3)
 .
.
(4)
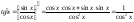 .
.
(6)
 .
.
(7)

(8)

(9)
 (5)
– самостоятельно.
(5)
– самостоятельно.
Дифференциал функции.
ОПР. Функция
 называется дифференцируемой в точке
называется дифференцируемой в точке
 ,
если ее приращение можно представить
в виде:
,
если ее приращение можно представить
в виде:
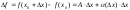 ,
где
,
где
 - б.м.ф. в точке
- б.м.ф. в точке
 .
.
ОПР. Главная
линейная часть приращения , величина
 ,
называется дифференциалом функции
,
называется дифференциалом функции
 в точке
в точке
 .
.
ТЕОРЕМА 3.
Существование
производной функции
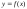 в точке
в точке
 является необходимым и достаточным
условием ее дифференцируемости.
является необходимым и достаточным
условием ее дифференцируемости.
ДОК. (1) Пусть функция
 дифференцируема. Тогда
дифференцируема. Тогда
 и
и
 .
.
(2)
Если функция
 имеет производную
имеет производную
 ,
тогда по теореме о связи
,
тогда по теореме о связи
 ,
где
,
где
 -
б.м.ф., т.е.
-
б.м.ф., т.е.
 ,
при
,
при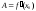 .
.
СЛЕДСТВИЕ.
Дифференциал функции
 имеет вид
имеет вид
 .
.
Функция
 имеет производную, равную 1, поэтому
имеет производную, равную 1, поэтому
 .
Тогда
.
Тогда
 .
.
ГЕОМЕТРИЧЕСКИЙ смысл дифференциала.
Уравнение
касательной, проведенной к графику
функции
 в точке
в точке
 ,
имеет вид:
,
имеет вид:
 .
.
Приращение
ординаты касательной, соответствующей
изменению аргумента на
 равно
равно
 ,
т.е. значению дифференциала
,
т.е. значению дифференциала
 .
.
ИНВАРИАНТНОСТЬ ФОРМЫ дифференциала.
Если
 - функция независимой переменной
y
, то ее
дифференциал имеет форму
- функция независимой переменной
y
, то ее
дифференциал имеет форму
 .
Если
.
Если
 -
сложная функция и
-
сложная функция и
 ,
то
,
то
 ,
,
т.е. форма записи дифференциала не зависит от того, является ли y независимой переменной или функцией другой переменной. Это свойство дифференциала называется его инвариантностью.
Теорема о связи функции, имеющей предел и бесконечно малой функции
Для того, чтобы
функция
 имела предел в точке a
равный А,
необходимо и достаточно, чтобы имело
место представление :
имела предел в точке a
равный А,
необходимо и достаточно, чтобы имело
место представление :
 ,
где
,
где
 -
бесконечно малая функция в точке a
.ДОК. (1) Если
-
бесконечно малая функция в точке a
.ДОК. (1) Если
 ,
то функция
,
то функция
 б.м.ф.
б.м.ф.
Действительно (2)
(2)

 .
.
Арифметическая теорема о пределах
Если
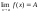 ,
,
 ,
то
,
то
(1)

(2)
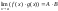 (3)
(3)
 .
.
ДОК. (2) По теореме
о связи
 ,
,
 ,
где функции
,
где функции
 и
и
 - бесконечно малые функции. Тогда
- бесконечно малые функции. Тогда
 где
где
 бесконечно малая функция
бесконечно малая функция
