33. Минимизация автомата
Каждый остаточный оператор реализуется
в некотором состоянии автомата. Отсюда
следует, что у любого автомата
,
реализующего ограниченно-детерминированный
оператор
,
число состояний
не меньше числа различных остаточных
операторов
оператора
:
.
(13)
Автомат с наименьшим числом состояний, реализующий ограниченно-детерминированный оператор , называется минимальным автоматом оператора .
Построенный при доказательстве последней
теоремы автомат
– минимальный.
Теорема. Минимальный автомат единственен с точностью до обозначения состояний.
Из теоремы следует признак минимальности
автомата: автомат будет минимальным,
если для любых двух его состояний
и
реализуемые в этих состояниях остаточные
операторы различны.
Задача минимизации автомата: для данного автомата построить минимальный автомат, реализующий ограниченно-детерминированный оператор . Рассмотрим алгоритм ее решения.
Пусть
.
В процессе работы алгоритма строятся
разбиения множества
на непересекающиеся классы:
.
На очередном шаге алгоритма происходит измельчение предыдущего разбиения до тех пор, пока это возможно. Классы разбиения после завершения алгоритма будут состояниями минимального автомата.
1-й шаг. Состояния и отнесем к одному классу, если
.
Получим разбиение
:
.
-й
шаг. Пусть на
-ом
шаге получено разбиение
:
.
Состояния и отнесем к одному классу нового разбиения, если выполнены два условия:
и входят в один класс предыдущего разбиения ;
для каждого символа состояния
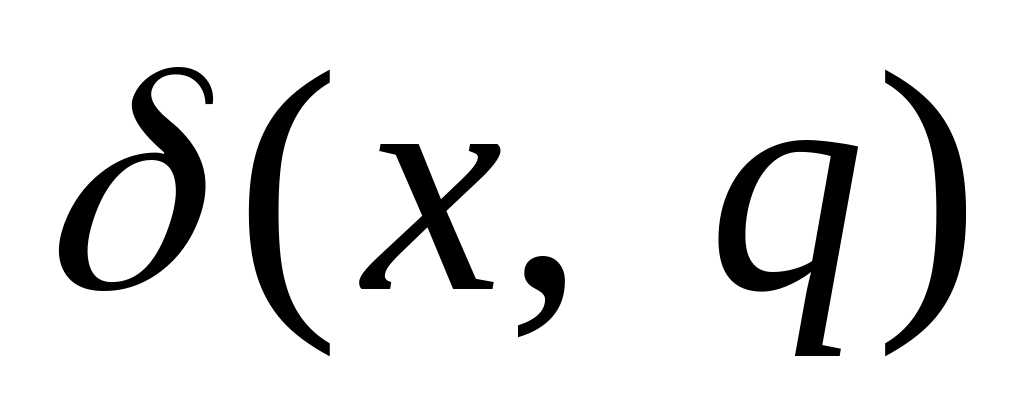и
входят в один класс предыдущего разбиения
.
Обозначим через
класс, в который входит состояние
.
Тогда условия 1) и 2):
;
.
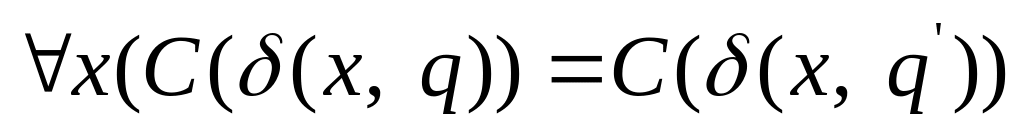Алгоритм заканчивает работу, когда на
некотором шаге
не произойдет дальнейшего измельчения
разбиения:
.
Последнее разбиение
:
.
Тот факт, что алгоритм закончил работу можно выразить следующим образом:
.
Строим автомат
:
,
,
,
,
.
Автомат реализует тот же словарный оператор, что и автомат , и является минимальным.
34. Понятие формального языка
До начала XX века наука о языках – лингвистика – сводилась в основном к изучению естественных языков (русского, английского, латинского и т. д.), их классификации, выяснению сходств и различий между ними.
Возникновение и развитие метаматематики, изучающей по существу язык математики, логико-философские исследования языка науки, предпринятые Л. Виттгенштейном, Р. Карнапом и другими в 20-30 гг. XX века, идеи структурного подхода к лингвистике привели в 30-х годах к существенно более широкому представлению о языке, при котором под языком понимается всякое средство общения, состоящее из
знаковой системы, т. е. множества допустимых последовательностей знаков;
множества смыслов этой системы;
соответствия между последовательностями знаков и смыслами, делающего осмысленными допустимые последовательности знаков.
Знаками могут быть буквы алфавита, математические обозначения, звуки и т. д. Наука об осмысленных знаковых системах называется семиотикой. Наиболее продвинутыми являются исследования знаковых систем, в которых знаками являются символы алфавитов, а последовательностями знаков – тексты. К таким знаковым системам относятся естественные языки, языки науки, а также языки программирования. Именно интерес к языкам программирования, совпавший с новыми подходами в структурной лингвистике и необходимостью решать задачу машинного перевода естественных языков, привел в 50-х гг. к возникновению новой науки – математической лингвистики, которая рассматривает языки как произвольные множества осмысленных текстов.
Правила, определяющие множества текстов, образуют синтаксис языка; описание множества смыслов и соответствия между тексами и смыслами – семантику языка. Наибольших успехов математическая лингвистика достигла в изучении синтаксиса, где за последние 30 лет сложился специальный математический аппарат – теория формальных грамматик.
С точки зрения синтаксиса язык понимается не как средство общения, а как множество формальных объектов – последовательностей символов алфавита, которые в теории алгоритмов и формальных систем называют словами. Язык, понимаемый как множество слов, будем называть формальным языком.