16Поняття поверхні
р-ня 1- р-ня поверхні, якщо в цьому р-ні задовольняє кожна точка поверхні і кожна точка, що не лежить на поверхні не задовольняє цього р-ня. Поверхня-це геометричне місце точок x, y,z, що задовольняють р-ня 1.
р-ня 1: Ax+ By+Cz+D=0
Якщо дві площини задаються загальними р-нями, то кут між площинами знаходиться як кут між їхніми векторами нормалей
Умова перпендикулярності площин: 2 площини перпендикул тоді, коли є перпендикулярними їхні вектори нормалей, тобто:
Умова паралельності площин: 2 площини паралельні тоді, коли їх вектори нормалей будуть колінеарними
Геометричний зміст лінійного р-ня з 3 невідомими: якщо в просторі з введеною системою координат кожна площина виражена лінійним р-ням Ax+ By+Cz+D=0 то навпаки: кожне лінійне р-ня виражає площину.
Доведення
У нас є деяка площина; вектор нормалі n {A,B,C}; Mo (x0,y0,z0) ;
Нехай М – довыльна точка площини з корд x,y,z ; тоді вектор МоМ лежатиме вплощині і буде перпенд вектору n
отже, вектор МоМ * n =0
вектор МоМ ={x-x0;y-y0;z-z0}
Вектор МоМ * вектор n=A(x-x0) + B(y-y0) + C(z-z0)=0 (2)
Оскільки М- довільна точка на площині, то (2) – р-ня площини.
1
7.
17.
ОР перпенд площині
Р |op|=p
М вектор S – орт вектора ор
|S|=1
вектор S= {cosα;cosβ;cosγ}
візьмемо довільну точку на площині М(z;y;z)
пр. – орвектор ОМ
(x,y,z)( cosα;cosβ;cosγ)=p
xcosα+ycosβ+zcosγ-p=0
Оскільки це р-ня виконується для довільної точки М, то воно представляє собою р-ня площини, яке назив. нормальним.
Відхиленням точки А від площини називається число δА і що= відстані від точки до площини, взятої зі знаком +, якщо точка й початок координат лежать по різні сторони площини. З означення відхилення випливає, що dA= |δА|
Знаходження відстані від точки до площини: 1) зводимо р-ня площини до нормального виду
2) підставляємо координати точки в нормальне р-ня площини й отримане число беремо по модулю
умова перп і парал – питання 16
1
8
q M
q={L;m;n}
Mo
Mo(Xo,Yo,Zo)
х-х0/L= y –yo/m = z-z0/n – канонічне рівняння прямої
кут між прямими , умова парал і перпенд. прямих:
х-х1/L1= y –y1/m1 = z-z1/n1
х-х2/L2= y –y2/m2 = z-z2/n2
q
1
= {L1;m1;n1};
q2 = {L2;m2;n2}
cosϕ
у
мова
парал: q1
|| q2 
умова перпендикулярності: q1q2 = 0: L1L2 + m1m2 + n1n2 =2
кутом між прямою і площиною називається кут між даною прямою та проекцією цієї прямої на задану площину
23.
Озн. δ-околом точки А назив. множина всіх х {х:ӏх-аӏ<δ}.
Озн. Число b назив. границею ф-ції f(x), х→а, якщо для як завгодно малих f(x) ε>0 існує таке δ, що як тільки ӏх-аӏ<δ ӏf(x)-bӏ<ε: при х →а lim f(x)=b.
Озн. Число b назив. границею ф-ції при х→∞ при довільному ε>0 ІхІ>δ Іf(x)-bІ <ε: при х→∞ lim f(x)=b.
Озн. Якщо в позначенні границі будемо вважати,що х→а, х>а,то така границя назив. правосторонньою,якщо ж при х→а х залишається <за а, то лівосторонньою.
Теорема.Для того, щоб для ф-ції y=f(x) існувала скінченна границя необхідно і достатньо,щоб існували односторонні границі і вони були рівні між собою.
Теорема1:Якщо існує скінченна границя: при х→а lim у(x)=b,то ф-ція обмежена в околі т.А.
Теорема2(про 2 міліціонерів):Нехай для ф-цій u(x), v(x),y(x) в усіх точках з обл. визначення D виконується u(x)≤y(x)≤v(x),аЄD: при х→а lim u(x)=b, lim v(x)=b, тоді для ф-ції у(х) буде існувати границя : при х→а lim у(x)=b.
Теорема3:Якщо при х→а ф-ція у(х)≥0 і має скінченну границю lim у(x)=b,то число b≥0.
Теорема4:Якщо в обл.визн.D u(x)≥v(x),аЄD при х→а lim u(x)=b1, lim v(x)=b2,тоді b1≥b2.
Теорема5:Якщо для всіх точок обл.визн.D, Іу(х)≤МІ, ф-ція у(х) зростає і обмежена, аЄD,то при х→а lim у(x)=b і b≤М.
24.
Озн.Ф-ція α(х) назив.нескінченно малою при х→а, якщо при х→а lim α(x)=0. Аналогічно при х→∞ .
Т1.Якщо ф-цію можна записати у(х)=b+α(х), де α(х)-неск.мала при х→а ,а b-скінченне число, то це означає,що при х→а lim у(x)=b і навпаки, якщо для у(х) існує границя,що=b, то у(х) можна записати у(х)=b+α(х).
Т2.Якщо α1(х),α2(х)-неск.малі при х→а, тоді іх сума α1(х)+α2(х) буде неск. малою при х→а.
Зауваж.:Теорема справедлива для скінченної суми нескінченно малих ф-цій.
Т3. Якщо при х→а α(х)-нескюмала, а z(х)-обмежена, то α(х)z(х) буде нескюмалою при х→а.
Т4.Якщо неск.мала α(х), х→а,а границя ф-ції z(х)=b, то α(х)/z(х) буде нескюмалою при х→а.
Озн.Ф-ція β(х)назив. неск.великою при х→а,якщо границя β(х)=∞,тобто для будь-яких як завгодно великих М існує δ,що як тільки Іх-аІ<δ Іβ(х)І>М.
Теорема про зв‘язок неск.мал. і неск.вел.ф-цій:
Якщо при х→а α(х)-неск мала ф-ція,то при х→а β(х)=1/α(х) буде неск.великою.
25.
Т1.Якщо при х→а границя ф-ції u(х)=b1, а границя ф-ції v(х)=b2,то при х→а границя суми цих ф-цій lim(u(x)+v(x)) буде= сумі границь lim u(x)+lim v(x).
Доведення:З існування границі дляф-ції u(х) виплив. u(х)=b1+α1(х), де α1(х)→0 при х→а, аналог. З існування границі для ф-ції v(х): v(х)=b2+α2(х), α2→0 при х→а,додамо u(x)+v(x)=(b1+b2)+(α1+α2).За теор.про неск.малі2 α1+α2 буде неск.малою при х→а, тоді за теор.про неск малі1 остан.рівність означає,що при х→а lim (u(x)+v(x))=b1+b2.Доведено.
Т2. При х→а lim u(x)=b1, lim v(x)=b2,то при х→а буде існувати lim u(x)v(x)=lim u(x)lim v(x).Довед.: u(x)=b1+α1(x), α(x)→0 при х→а, v(x)=b2+α2(x), α2→0 при х→а. u(х)*v(x)=(b1+α1(x))(b2+α2(x))=b1b2+α1(x)b2+b1α2(x)+ α1(x)α2(x).Оскільки b1,b2 –сталі, то вони обмежені, отже за теор. про неск. малі3 α1(х)b2, b1α2(x)-неск.малі. α1(х)α2(х)-неск.малі.Сума неск.малих-неск.мала.Отже Т1, при х→а lim u(x)v(x)=b1b2.
Т3. Якщо при х→а lim u(x)=b1,lim v(x)=b2≠0,то при х→а існує lim u(x)/v(x)=lim u(x)/lim v(x).
26. Перша чудова границя та її наслідки:
Наслідки:
27. Друга чудова границя та її наслідки:
1)
2)
28. Неперервні ф-ї: означення, властивості неперервних функцій.
1) f(x)
наз.
Неперервн в точці
,
якщо вона визначена в т.
та
в деякому її околі і
2) щоб
була
неперерв. В т.
,
треба, щоб була границя справа, зліва
і:
та
,
.
3) т. розриву першого
роду: існують границі
та
але
,
Пр:
Другого роду: т., де границя: =
хоча
б з одного боку, або не існує.Пр:
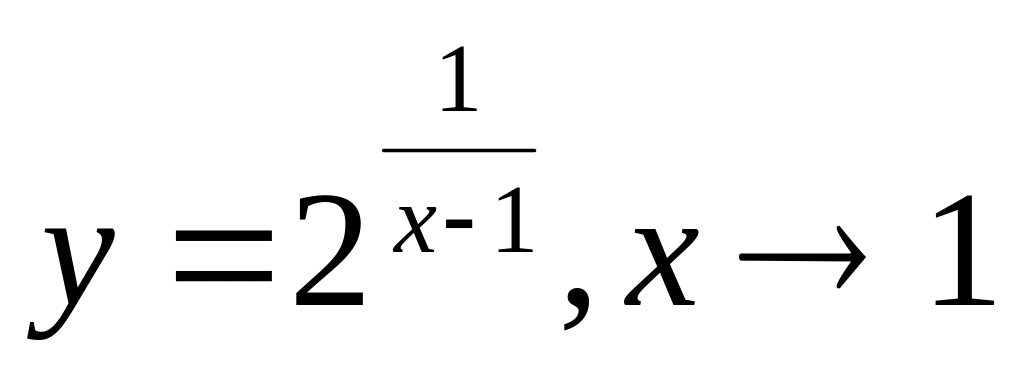
29. Порівняння нескінченно малих ф-цій. Теореми про еквівалентні функції.
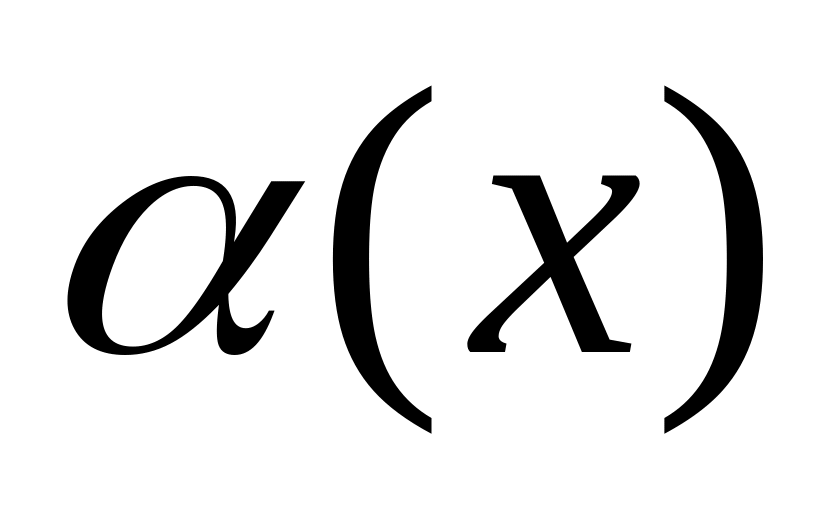є
н.м. вищого порядку
,
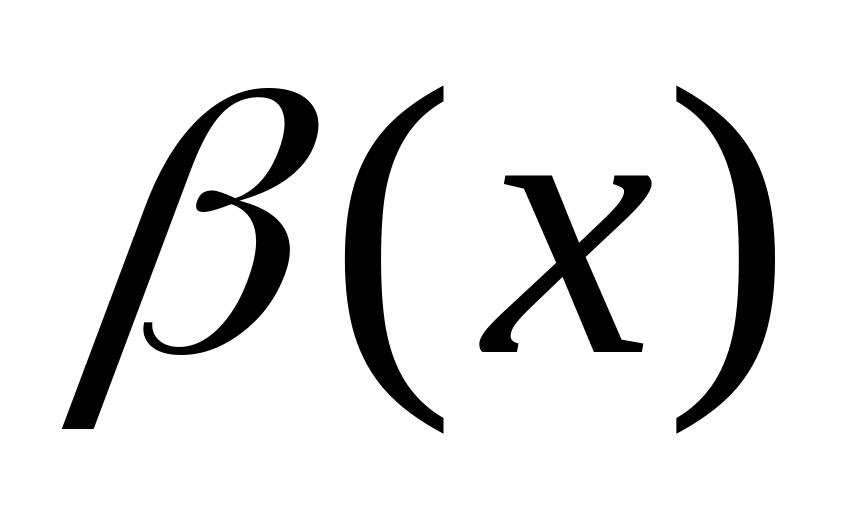якщо:
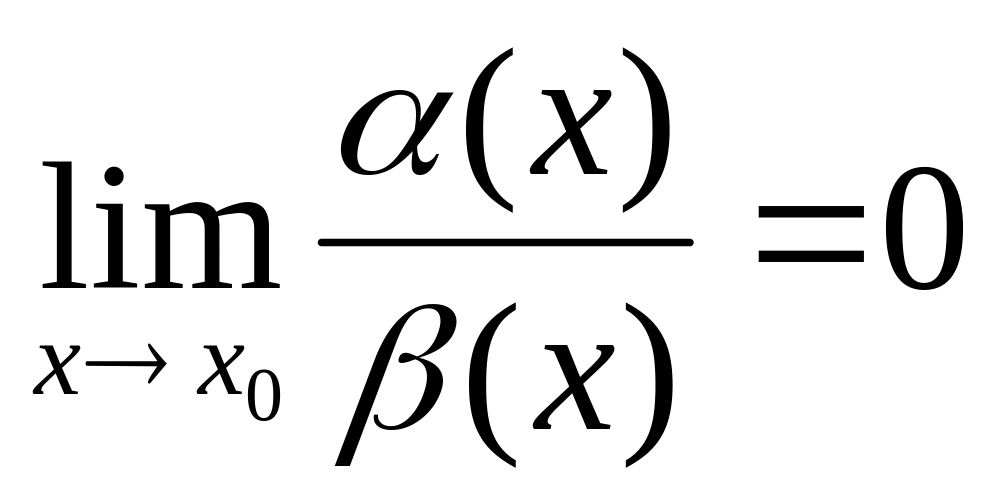тоді
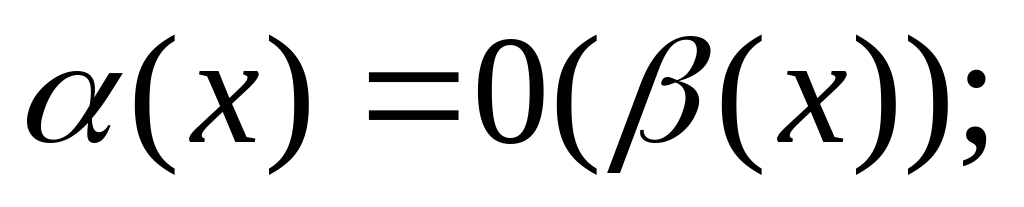0-малаОдного порядку:
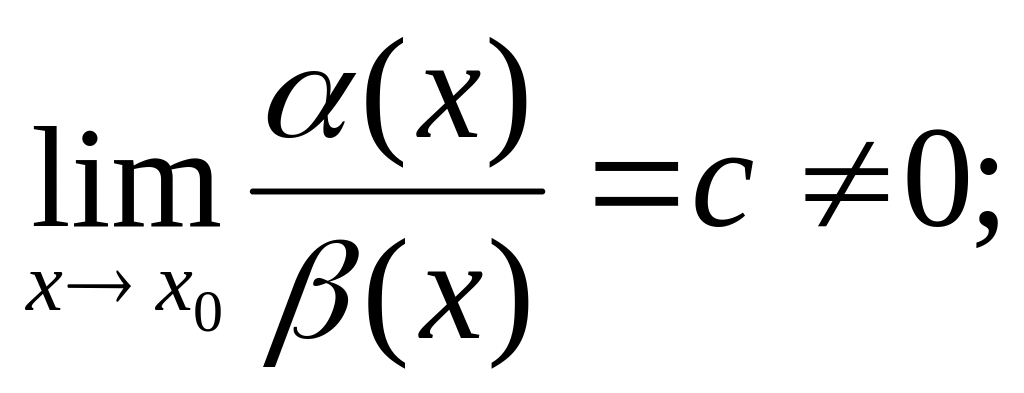
подібно
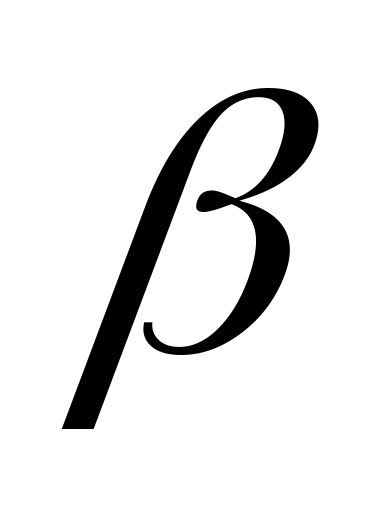
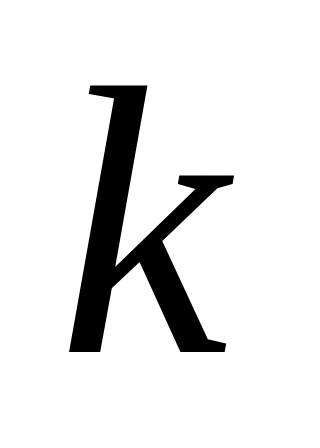порядок
від
:
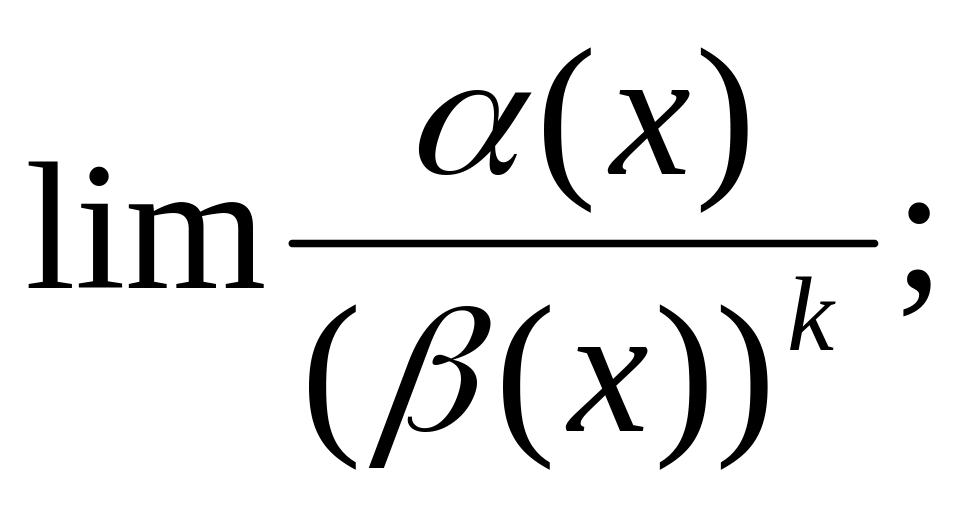
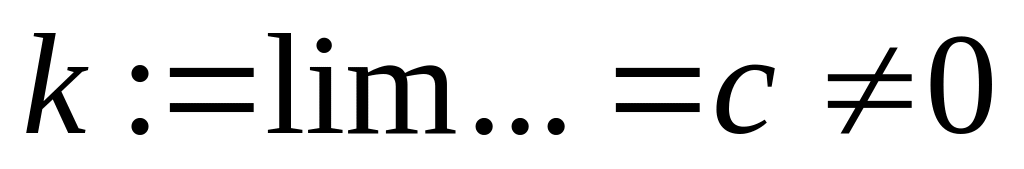
2.1) Вліст:
-
=
0(
);
подібне
2.2)
под.
;
под.
3.1)
под.
:
-неперерв
із(2) еквівалент.
3.2)
:
