
- •1.Системи рівнянь з двома невідомими. Визначники другого порядку, третього порядку та їх властивості.
- •2. Системи трьох рівнянь з трьома невідомими. Формули Крамера. Поняття про визначник n-го порядку.
- •3.Напрямлені відрізки. Система координат на площині та в просторі.
- •5. Вектори, основні поняття. Лінійні операції над векторами та їх властивості. Напрямлені косинки вектора.
- •6. Проекція вектора на вісь. Деякі вл-ті проекціі:
- •8.Означення базиса.Розклад вектора за коорд.Базисом.Декартові прям.Коорд вектора.
- •9.Скалярний добуток та його вл-ті.
- •10.Векторний добуток та вл-ті:
- •Дистрибутивність
- •Властивості
- •11.Векторний добуток
- •Властивості векторного добутку
- •16Поняття поверхні
6. Проекція вектора на вісь. Деякі вл-ті проекціі:



![]() Q Через початок
проведемо
Q Через початок
проведемо ![]() ,
тоді проекція
на u наз. Число що дор.довж
.
,
тоді проекція
на u наз. Число що дор.довж
.
Пр(u)a=|
![]() *
*![]()
U Q - гострий ( +) , тупий(-)
Вл-ть1:
Пр(u)( ![]() Пр(u)
Пр(u) ![]() +
Пр(u)
+
Пр(u) ![]()
Вм-ть:
Пр(u)( ![]() λ*
Пр(u)(
λ*
Пр(u)( ![]()
7-8.Лінійна залежність і незалежність векторів.Необхідна і достатня умова лінійної незалежності трьох вектрів.
Щоб вектори були лінійно залежними, необх. і дост. щоб вони були компланарні.
1).![]() –Лін. Залежні.
–Лін. Залежні.
![]() ,
,
![]() ,
,![]() – не дорівн. 0.
– не дорівн. 0.
![]() 0
;
0
; ![]() =
-
=
-![]()
![]()
![]() =
-
=
-
![]() ;
;
=![]() +
+![]() з цієї рівності, вектор
є діагоналлю паралелограма:
з цієї рівності, вектор
є діагоналлю паралелограма:



 -
зведені до одного початку,
-
зведені до одного початку,
о тже
вони компланарні.
тже
вони компланарні.
![]()
![]()
![]() =0
- ці вектори лінійно залежні.
=0
- ці вектори лінійно залежні.
2).![]() =0
- ці вектори лінійно не залежні.
=0
- ці вектори лінійно не залежні.
8.Означення базиса.Розклад вектора за коорд.Базисом.Декартові прям.Коорд вектора.
Будь-яка впорядкована трійка некомпланарних векторів наз.базисом у просторі.
Числа λ1, λ2, λ3- наз.коорд.вектора ā в базисі a1,a2,a3, а саме ā= λ1 ā1+ λ2 ā2 + λ3 ā3 розкладений ā по базису a1,a2,a3.
Три однакові взаемоперпендикулярні вектори <ī, ĵ,ĸ> утв.базис, наз. Декартовим(прямокутним) базисом , тоді будь-як ā=А(х) ī+А(у) ĵ+А(z) ĸ={ А(х), А(у) , А(z) }-дек.коорд.вектора.
9.Скалярний добуток та його вл-ті.
О зн:Скал.добут.
ā і b – наз.Число
що позн. (ā, b)
зн:Скал.добут.
ā і b – наз.Число
що позн. (ā, b)
ā
 b= |ā|*|b|*
b= |ā|*|b|*![]() ā
ā ![]()
b
ā b=|ā|*Пр(ā)b або ā b=|b|* Пр(b) ā
Вл-ті:
1)Комутативність ā b = b ā
2)Асоціативність (![]() ā)b=
ā)b=![]() āb)
āb)
3)Дистрибутивність (ā +b)ĉ= ā ĉ+ b ĉ
4) ā
![]() b
= ā b=0
b
= ā b=0
10.Векторний добуток та вл-ті:
- Наз.вектор [ā b] або (ā* b), який задов:
1)Довж:
|[ā b]|=|ā|*| b
|*![]()
2)
[ā b]![]() ā
ā
[ā b] b
Властивості:
ā ||b = [ā b]=0
|[ā b]|=Sпар-ма
Антикомутат: [ā b]= - [b ā]
[ ā;b]=
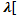 āb]
āb]Дистрибутивність
[(ā +b),ĉ]= [ā ,ĉ]+ [b, ĉ]
векторний добуток-двох векторів назив.вектор, який позначається так [ab] або (а*b) і задовольняє такі умови:1) [ab]=a*b*sinD 2) [ab]перпен.a [ab]перпендик b.
3)напрями вектора визнач. правилом правої руки
Властивості: 1) і достатньою умовою колінеарних векторів є aIIb тобто[ab]=0
1част.)aIIb D=0 і D=П sin0=sinП=0
[[ab]]=0,а отже маємо нульовий вектор.
2част.) відомо що вект.добуток =0.
Є 2 варіанта: 1)серед a і b є нульовий, тобто [a]=0 або [b]=0. Тоді [[ab]]=0 доведено.
2) серед векторів немає нульового:[[ab]]=0 тобто sinD=0 D=0 D=П
Тобто вектори колінеарні.
11.Мішаний добуток трьох векторів назив. число що познач. авс = [ab]c
властивості :
1)геометрична: якщо а,в,с не компленарні ,то модуль їх мішаного добутка дорівнює об’єму паралелепіпеда побудованого на цих векторах
доведення:розгл.[ав]с=Sпар *cosD=+-V;
e-орт вектора вектор.добутка [ab] тобто перпенд ю площині де а=1 в=1 е=1
отже:S(+-h)=+-V
V=[[ab]c]=[abc]
Зауваження:Vтетр=1/6 abc
2) три вектори компленарні тоді коли їх міш.добуток=0
3)[ab]c=a[bc]
10.Скалярний добуток
Скалярний
добуток (англ. dot
product, англ. scalar
product, нім. Skalarprodukt, рос. скалярное
произведение) —
математична операція над двома векторами,
результатом якої є скаляр.
Скалярний добуток векторів ![]() та
та ![]() обчислюється
за формулою:
обчислюється
за формулою:
![]()
де ![]() та
та ![]() є довжинами
векторів,
а
є довжинами
векторів,
а ![]() дорівнює косинусу кута
між цими векторами. Як і у випадку
звичайного множення,
знак множення можна не писати:
дорівнює косинусу кута
між цими векторами. Як і у випадку
звичайного множення,
знак множення можна не писати: ![]() =
= ![]() .
.
Скалярним добутком двох векторів — називається число, рівне добутку довжин цих векторів на косинус кута між ними.
