16. Лду второго порядка

основные понятия

Определение: уравнение вида y" +p(x)y'+q(x)y=f(x) (1) где y- искомая функция, y" и y' – производные 2 и 1 порядка соответственно, P(x), q(x), f(x)- непрерывные функции на некотором интервале (a;b) называется ЛДУ 2 порядка.

Если f(x)=0, то уравнение называется ЛОДУ. В противном случае ЛНДУ.

Если разрешить (1) относительно y", то получим: y"= -P(x)y' – q(x)y+f(x).

Очевидно, что полученные уравнение является частным случаем уравнения: y"=f(x,y,y') и удовлетворяет условиям теорем о существовании и единственности решения.

______________________

17. Линейные однородные дифференциальные 2 порядка

Рассмотрим y"+P(x)y'+q(x)y=0 (1) и установим некоторые свойства его решений.

теорема 2.1.: если функции y₁=y₁(x) и y₂=y₂(x) является частными решениями уравнения (2.1), то функция: y=C₁y₁(x)+C₂y₂(x), где С₁ и С₂ произвольные постоянные также являются решением данного уравнения.

Доказательство

подставим y=C1y1(x)+C2y2(x) и ее производную в уравнение (2.1)(в левую часть), то получим:

(C₁y₁+C₂y₂)"+P(x)(C₁y₁+C₂y₂)'+q(x)(C₁y₁+C₂y₂)=C₁y₁"+C₂y₂"+C₁P(x)y₁'+C₂P(x)y₂'+C₁q(x)y₁+ C₂q(x)y₂=C₁[y₁"+P(x)y₁'+q(x)y₁]+C₂[y₂"+P(x)y₂'+q(x)y₂]=*

Т.к. по условию теоремы функции y₁ и y₂ являются решениями (2.1)

Выражение в [ ] значит = 0: *=С₁*0+С₂*0=0.

Т.о. функция y=C₁y₁(x)+C₂y₂(x) является решением уравнения (2.1)

Докажем теперь, что при некоторых условиях функция y=C₁y₁(x)+C₂y₂(x) является общим решением

Введем новые понятия

Определение: функции y₁(x) и y₂(x) называются линейно зависимыми на интервале (a;b), если существуют такие числа α₁ и α₂, из которых хотя бы одно отлично от 0, что для всех x принадлежащих (a;b) имеет место равенство: α₁y₁'(x) + α₂y₂'(x)=0 (2.3)

Очевидно, что y1 и y2 линейно зависимы т.т.т., когда они пропорциональны: для всех x принадлежащих (a;b) y₁/y₂=λ, или y₁=λy₂, λ= const

Определение: функции y₁(x) и y₂(x) называются линейно независимыми на интервале (a;b), если (2.3.) выполняется т.т.т., когда α₁=α₂=0

______________________

18. Линейная зависимость функций. Определитель Вронского, его свойства. Фундаментальная система решений.

Средством изучения линейной зависимости системы функций является так называемый определитель Вронского (Вронскиан)

Для 2-х дифференциальных уравнений y₁=y₁(x) и y₂=y₂(x) определитель Вронского имеет вид:

W(x)=

Теорема 2.2.: если дифференциальные функции y₁(x) и y₂(x) линейно зависимы на (a;b), то составленный из них определитель Вронского на этом интервале тождественно равен 0

Т.к. y₁(x) и y₂(x) линейно зависимы, то в равенстве: α₁y₁(x)+α₂y₂(x)=0 α₁ или α₂ ≠0

Пусть α₁≠0, тогда y₁=-(α₂/α₁)y₂

Поэтому для всех x принадлежащих (a;b): W(x)= = =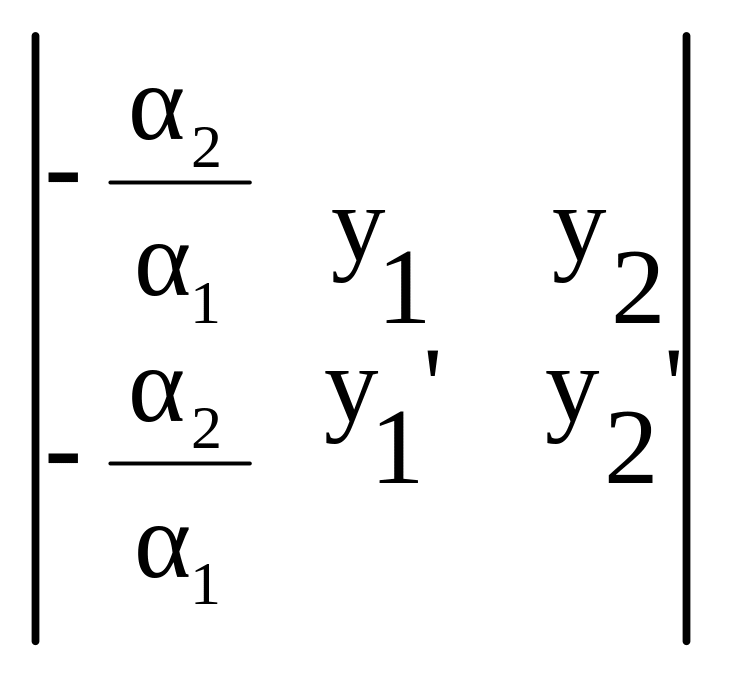0

что и требовалось доказать

Теорема 2.3. Если решения y₁(x) и y₂(x) уравнения (2.1) линейно независимы на интервале (a;b), то составленный из них определитель Вронского отличен от 0 на этом интервале

замечание: из теорем 2.2. и 2.3. следует, что W(x)≠0 ни в одной точке (a;b) т.т.т., когда частные решения линейно независимы.

совокупность любых двух линейно независимых на интервале (a;b) частных решений y₁(x) и y₂(x) уравнения (2.1) определяют фундаментальную систему решений этого уравнения: любое произвольное решение м.б. получено как комбинация y=α₁y₁(x)+α₂y₂(x). Теперь можно сказать, при каких условиях функция y=C₁y₁(x)+C₂y₂(x) будет общим решением.

______________________