9. Интегрирующий множитель
Однако уравнение P(x,y)dx+Q(x,y)=0 можно привести к уравнению в полных дифференциалах умножением его на некоторую функцию t(x,y), называемую интегрирующим множителем. Чтобы уравнение:
t(x,y)*P(x,y)dx+t(x,y)*Q(x,y)dy=0 было уравнением в полных дифференциалах должно выполняться условие: ∂/∂y(t(x;y)*P(x;y))=∂/∂x(t(x;y)*Q(x;y))
Выполнив дифференцирование:
∂t/∂y*P-∂t/∂x*Q=t(∂Q/∂x-∂P/∂y) (6)
Проведя подобные слагаемые, получим:
∂t/∂y*P-∂t/∂x*Q=t(∂Q/∂x-∂P/∂y) (6)
Для нахождения t(x,y) надо проинтегрировать полученное дифференциальное уравнение в частных производных. Этот процесс достаточно сложный. Однако нахождение интегрального множителя может быть упрощено если допустить существование t как функции только одного аргумента (или х или у). Пусть например t=t(x).
Тогда (6) примет вид:
-∂t/∂x*Q=t(∂Q/∂x-∂P/∂y)
dt/t=((∂P/∂y-∂Q/∂x)/Q)dx
Отсюда t(x) будет равным:
∫dt/t=∫((∂P/∂y-∂Q/∂x)/Q)dx
t(x)=exp(∫((∂P/∂y-∂Q/∂x)/Q)dx)
При этом (∂P/∂y-∂Q/∂x)/Q должно зависеть только от х.
аналогично получаем, что если t=t(y), то t(y)=exp(∫((∂P/∂x-∂Q/∂y)/Q)dy)
А подынтегральное выражение должно зависеть только от y.
______________________
10. Приближенное решение ду первого порядка методом Эйлера
Пусть дано дифференциальное уравнение y’=f(x;y) (1)
и требуется найти частное решение, удовлетворяющее условию y(x0)=y0. Это означает, что надо найти интегральную кривую, проходящую через т.М0(x0,y0).
Суть метода Эйлера заключается в том, что интегральную кривую можно построить в виде ломаной, состоящей из прямолинейных отрезков.
Рассмотрим способ построения этой ломаной на отрезке [x0,b].
Р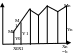
азделим
[x0,b]
на n
равных частей точками х0, х1, х2 , …хn=b
и через эти точки проведем прямые,
параллельные Oy.
И
з
начальной т.М0(x0,y0),
которая принадлежит интегральной кривой
будем вести ломаную, заменяющую
интегральную кривую. Подставим в правую
часть (1) координаты т.М0 и вычислим
угловой коэффициент касательной к
интегральной кривой в этой точке.
Из т.М0 проведем прямую с угловым коэффициентом К0 до пересечения с прямой х=х1 в т.М1 с координатами х1,у1.
Уравнение касательной М0М1 имеет вид: y-y0=K0(x-x0)/(2)
Примем т.М1 с координатами (x1,y1) за точку интегральной кривой . Т.к. эта точка лежит на прямой М0М1, то подставим вместо текущих координат (2) координаты т.М1.:
y1-y0=K1(x1-x0)(3)
Зная координаты т.М1 можно поставить их в уравнение (1) и найти К1=f(x1,y1).
Из т.М1 проведем прямую с угловым коэффициентом К1 до пересечения с прямой х1=x2 в т.М2(x2,y2) . Напишем уравнение прямой М1М2: y-y1=K1(x-x1)(4).
Т.к. т.М2(x2,y2) принадлежит прямой (4), то подставляя коэффициенты М2 в (4) получим:
y2-y1=K1(x2-x1).
Зная координаты т.М2 можно из уравнения (1) найти угловой коэффициент K2=f(x2,y2) и построить прямое М2М3 до пересечения с x=x3 в т.М3(x3,y3).
Этот процесс можно продолжить вплоть до получения координат вершины Mn(xn,yn).
Построенная таким образом ломаная М1,М2,…Мn представляет на отрезке [x0,b] приближенную интегральную кривую, проходящую через т.М0(x0,y0). Она называется ломаной Эйлера.
Ломаная Эйлера и интегральная кривая имеют общую М0(x0,y0). Отметим , что по мере удаления от этой точки отклонение ломаной от интегральной кривой можно увеличивать. Если отрезок [x0,b] Разделим на n равных частей, то h=(b-x0)/n называется шагом вычисления.
Очевидно, что уменьшение величины h увеличивает точность построения. Можно доказать, что при некоторых условиях относительно функции f(x,y) и при h0 приближенное решение стремится к точному решению данного уравнения, т.е ломаная будет стремиться к слиянию с интегральной кривой.
При построении ломаной Эйлера координаты ее вершин могут быть найдены непосредственно из чертежа. В этом случае метод ломанных Эйлера есть метод графического нахождения приближенного решения данного уравнения.
Значения ординат вершин ломаной рассматривать как приближенные значения искомого решения данного дифференциального уравнения. При этом как следует из арссмотренного способа построения ломаной ордината т.Мi+1(xi+1,yi+1) находится по формуле: yi+1=yi+1+Ki*h или yi+1=yi+1+f(xi,yi)*h (6).
______________________