30.3 Вынужденные колебания в среде без сопротивления, случай резонанса.

Рассмотрим ту же задачу, что и в предыдущем случае: колебание тела в среде без сопротивления, но будем считать, что на тело действует внешняя сила, изменяющаяся периодически.

То уравнение движения

, (11)

где

ЛНДУ-2 с постоянными коэффициентами

Для решения надо найти общее решение соответствующего ЛОДУ-2 и какое-нибудь частное решение ЛНДУ.

Общее решение уже нашли в пункте 1.

Найдем Xчн по виду правой части.

Так как k1,2 = ± wi здесь возможны случай:

1˚) пусть λ≠ω, то r = 0, то

Как видно из формулы результирующее движение складывается из двух колебаний с разными частотами, то оно не можыт быть колебательным.

Но, если λ и ω кратны, то это будет колебательное движение с частотой равной min(λ,ω). Кроме того если λ и ω близки по значению, то амплитуда второго значения в формуле (12) неограниченно велика, то тело будет совершать колебания с большим размахом. Этот случай называется резонансом. Его стараются исключить, так как возникает угроза целостности сооружения, но этот случай стараются воспроизвести в электромагнитных колебаниях.

Рассмотрим теперь этот случай резонанса

2˚) пусть λ = ω, k1,2 = ± λi, r = 1

В этом случае

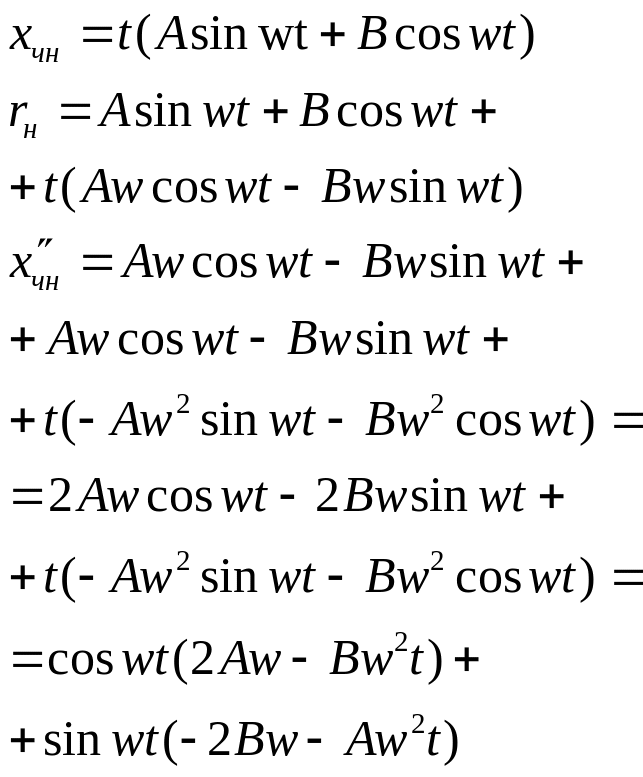
Для нахождения А и В надо подставить Xчн, X’чн, X”чн в уравнение (11).

Далее составим и решим систему уравнений относительно А и В, получим

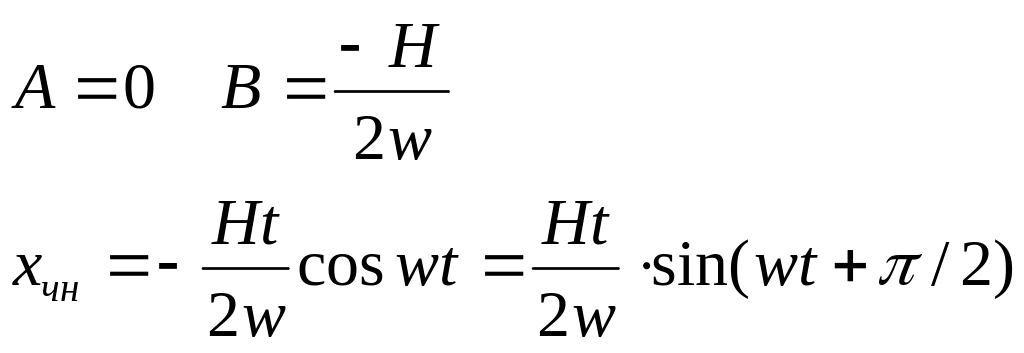
Следовательно, общее решение

Здесь результирующее движение тоже складывается из 2-х колебаний, но с одинаковыми частотами, то оно тоже будет колебанием с такой же частотой. Кроме того, если амплитуда второго слагаемого неограниченно растет, то общая амплитуда также неограниченно растет, то мы имеем явление резонанса в чистом виде. На практике такого не случается, так как нужно еще учитывать сопротивление среды. В этом случае явление резонанса состоит в том, что амплитуда результирующего колебания растет, если λ приближается к ω и достигает некоторого конечного максимума при неограниченном значении λ = λ0, близким к ω.

______________________

1. Обыкновенные дифференциальные уравнения. Основные определения и понятия (порядок уравнения, решение, общее и частное решение, задача Коши, теорема существования и единственности решения).

2. Геометрический смысл дифференциального уравнения первого порядка.

3. Уравнения с разделяющимися переменными.

4. Однородные дифференциальные уравнения первого порядка.

5. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.

6. Метод вариации произвольной постоянной.

7. Уравнение Я. Бернулли.

8. Уравнения в полных дифференциалах. Необходимое и достаточное условие.

9. Интегрирующий множитель.

10. Приближенное решение дифференциального уравнения первого порядка методом Эйлера.

11. Дифференциальные уравнения первого порядка высших степеней.

12. Дифференциальные уравнения второго порядка: основные понятия (решение, общее и частное решения, общий и частный интеграл).

13. Геометрический смысл дифференциального уравнения второго порядка.

14. Уравнения, допускающие понижение порядка (три типа).

15. Дифференциальные уравнения п-го порядка. Основные понятия.

16. Линейные дифференциальные уравнения второго порядка. Основные понятия.

17. Линейные однородные дифференциальные уравнения второго порядка. Свойство их решений.

18. Линейная зависимость функций. Определитель Вронского, его свойства. Фундаментальная система решений.

19. Теорема о структуре общего решения линейного дифференциального уравнения 2-го порядка.

20. Линейные однородные дифференциальные уравнения п-го порядка.

21. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами (три случая при решении характеристического уравнения)

22. Линейные однородные дифференциальные уравнения п-го порядка с постоянными коэффициентами.

23. Линейные неоднородные дифференциальные уравнения 2-го порядка. Теорема о структуре общего решения линейного неоднородного дифференциального уравнения 2-го порядка.

24. Метод вариации произвольных постоянных.

25. Теорема о наложении решений.

26. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и правой частью специального вида.

27. Линейные неоднородные дифференциальные уравнения п-го (п>2) порядка с постоянными коэффициентами и правой частью специального вида.

28. Системы дифференциальных уравнений, основные понятия (нормальная система, теорема Коши и др.).

29. Системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами.

30. Приложение линейных дифференциальных уравнений к изучению колебательных процессов: свободные колебания в среде без сопротивления, свободные колебания в среде с сопротивлением, вынужденные колебания в среде без сопротивления, случай резонанса.

1. Обыкновенные дифференциальные уравнения. Основные определения и понятия (порядок уравнения, решение, общее и частное решение, задача Коши, теорема существования и единственности решения).

2. Геометрический смысл дифференциального уравнения первого порядка.

3. Уравнения с разделяющимися переменными.

4. Однородные дифференциальные уравнения первого порядка.

5. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.

6. Метод вариации произвольной постоянной.

7. Уравнение Я. Бернулли.

8. Уравнения в полных дифференциалах. Необходимое и достаточное условие.

9. Интегрирующий множитель.

10. Приближенное решение дифференциального уравнения первого порядка методом Эйлера.

11. Дифференциальные уравнения первого порядка высших степеней.

12. Дифференциальные уравнения второго порядка: основные понятия (решение, общее и частное решения, общий и частный интеграл).

13. Геометрический смысл дифференциального уравнения второго порядка.

14. Уравнения, допускающие понижение порядка (три типа).

15. Дифференциальные уравнения п-го порядка. Основные понятия.

16. Линейные дифференциальные уравнения второго порядка. Основные понятия.

17. Линейные однородные дифференциальные уравнения второго порядка. Свойство их решений.

18. Линейная зависимость функций. Определитель Вронского, его свойства. Фундаментальная система решений.

19. Теорема о структуре общего решения линейного дифференциального уравнения 2-го порядка.

20. Линейные однородные дифференциальные уравнения п-го порядка.

21. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами (три случая при решении характеристического уравнения)

22. Линейные однородные дифференциальные уравнения п-го порядка с постоянными коэффициентами.

23. Линейные неоднородные дифференциальные уравнения 2-го порядка. Теорема о структуре общего решения линейного неоднородного дифференциального уравнения 2-го порядка.

24. Метод вариации произвольных постоянных.

25. Теорема о наложении решений.

26. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и правой частью специального вида.

27. Линейные неоднородные дифференциальные уравнения п-го (п>2) порядка с постоянными коэффициентами и правой частью специального вида.

28. Системы дифференциальных уравнений, основные понятия (нормальная система, теорема Коши и др.).

29. Системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами.

30. Приложение линейных дифференциальных уравнений к изучению колебательных процессов: свободные колебания в среде без сопротивления, свободные колебания в среде с сопротивлением, вынужденные колебания в среде без сопротивления, случай резонанса.

1. Обыкновенные дифференциальные уравнения. Основные определения и понятия (порядок уравнения, решение, общее и частное решение, задача Коши, теорема существования и единственности решения).

2. Геометрический смысл дифференциального уравнения первого порядка.

3. Уравнения с разделяющимися переменными.

4. Однородные дифференциальные уравнения первого порядка.

5. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.

6. Метод вариации произвольной постоянной.

7. Уравнение Я. Бернулли.

8. Уравнения в полных дифференциалах. Необходимое и достаточное условие.

9. Интегрирующий множитель.

10. Приближенное решение дифференциального уравнения первого порядка методом Эйлера.

11. Дифференциальные уравнения первого порядка высших степеней.

12. Дифференциальные уравнения второго порядка: основные понятия (решение, общее и частное решения, общий и частный интеграл).

13. Геометрический смысл дифференциального уравнения второго порядка.

14. Уравнения, допускающие понижение порядка (три типа).

15. Дифференциальные уравнения п-го порядка. Основные понятия.

16. Линейные дифференциальные уравнения второго порядка. Основные понятия.

17. Линейные однородные дифференциальные уравнения второго порядка. Свойство их решений.

18. Линейная зависимость функций. Определитель Вронского, его свойства. Фундаментальная система решений.

19. Теорема о структуре общего решения линейного дифференциального уравнения 2-го порядка.

20. Линейные однородные дифференциальные уравнения п-го порядка.

21. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами (три случая при решении характеристического уравнения)

22. Линейные однородные дифференциальные уравнения п-го порядка с постоянными коэффициентами.

23. Линейные неоднородные дифференциальные уравнения 2-го порядка. Теорема о структуре общего решения линейного неоднородного дифференциального уравнения 2-го порядка.

24. Метод вариации произвольных постоянных.

25. Теорема о наложении решений.

26. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и правой частью специального вида.

27. Линейные неоднородные дифференциальные уравнения п-го (п>2) порядка с постоянными коэффициентами и правой частью специального вида.

28. Системы дифференциальных уравнений, основные понятия (нормальная система, теорема Коши и др.).

29. Системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами.

30. Приложение линейных дифференциальных уравнений к изучению колебательных процессов: свободные колебания в среде без сопротивления, свободные колебания в среде с сопротивлением, вынужденные колебания в среде без сопротивления, случай резонанса.

1. Обыкновенные дифференциальные уравнения. Основные определения и понятия (порядок уравнения, решение, общее и частное решение, задача Коши, теорема существования и единственности решения).

2. Геометрический смысл дифференциального уравнения первого порядка.

3. Уравнения с разделяющимися переменными.

4. Однородные дифференциальные уравнения первого порядка.

5. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.

6. Метод вариации произвольной постоянной.

7. Уравнение Я. Бернулли.

8. Уравнения в полных дифференциалах. Необходимое и достаточное условие.

9. Интегрирующий множитель.

10. Приближенное решение дифференциального уравнения первого порядка методом Эйлера.

11. Дифференциальные уравнения первого порядка высших степеней.

12. Дифференциальные уравнения второго порядка: основные понятия (решение, общее и частное решения, общий и частный интеграл).

13. Геометрический смысл дифференциального уравнения второго порядка.

14. Уравнения, допускающие понижение порядка (три типа).

15. Дифференциальные уравнения п-го порядка. Основные понятия.

16. Линейные дифференциальные уравнения второго порядка. Основные понятия.

17. Линейные однородные дифференциальные уравнения второго порядка. Свойство их решений.

18. Линейная зависимость функций. Определитель Вронского, его свойства. Фундаментальная система решений.

19. Теорема о структуре общего решения линейного дифференциального уравнения 2-го порядка.

20. Линейные однородные дифференциальные уравнения п-го порядка.

21. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами (три случая при решении характеристического уравнения)

22. Линейные однородные дифференциальные уравнения п-го порядка с постоянными коэффициентами.

23. Линейные неоднородные дифференциальные уравнения 2-го порядка. Теорема о структуре общего решения линейного неоднородного дифференциального уравнения 2-го порядка.

24. Метод вариации произвольных постоянных.

25. Теорема о наложении решений.

26. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и правой частью специального вида.

27. Линейные неоднородные дифференциальные уравнения п-го (п>2) порядка с постоянными коэффициентами и правой частью специального вида.

28. Системы дифференциальных уравнений, основные понятия (нормальная система, теорема Коши и др.).

29. Системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами.

30. Приложение линейных дифференциальных уравнений к изучению колебательных процессов: свободные колебания в среде без сопротивления, свободные колебания в среде с сопротивлением, вынужденные колебания в среде без сопротивления, случай резонанса.

1. Обыкновенные дифференциальные уравнения. Основные определения и понятия (порядок уравнения, решение, общее и частное решение, задача Коши, теорема существования и единственности решения).

2. Геометрический смысл дифференциального уравнения первого порядка.

3. Уравнения с разделяющимися переменными.

4. Однородные дифференциальные уравнения первого порядка.

5. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.

6. Метод вариации произвольной постоянной.

7. Уравнение Я. Бернулли.

8. Уравнения в полных дифференциалах. Необходимое и достаточное условие.

9. Интегрирующий множитель.

10. Приближенное решение дифференциального уравнения первого порядка методом Эйлера.

11. Дифференциальные уравнения первого порядка высших степеней.

12. Дифференциальные уравнения второго порядка: основные понятия (решение, общее и частное решения, общий и частный интеграл).

13. Геометрический смысл дифференциального уравнения второго порядка.

14. Уравнения, допускающие понижение порядка (три типа).

15. Дифференциальные уравнения п-го порядка. Основные понятия.

16. Линейные дифференциальные уравнения второго порядка. Основные понятия.

17. Линейные однородные дифференциальные уравнения второго порядка. Свойство их решений.

18. Линейная зависимость функций. Определитель Вронского, его свойства. Фундаментальная система решений.

19. Теорема о структуре общего решения линейного дифференциального уравнения 2-го порядка.

20. Линейные однородные дифференциальные уравнения п-го порядка.

21. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами (три случая при решении характеристического уравнения)

22. Линейные однородные дифференциальные уравнения п-го порядка с постоянными коэффициентами.

23. Линейные неоднородные дифференциальные уравнения 2-го порядка. Теорема о структуре общего решения линейного неоднородного дифференциального уравнения 2-го порядка.

24. Метод вариации произвольных постоянных.

25. Теорема о наложении решений.

26. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и правой частью специального вида.

27. Линейные неоднородные дифференциальные уравнения п-го (п>2) порядка с постоянными коэффициентами и правой частью специального вида.

28. Системы дифференциальных уравнений, основные понятия (нормальная система, теорема Коши и др.).

29. Системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами.

30. Приложение линейных дифференциальных уравнений к изучению колебательных процессов: свободные колебания в среде без сопротивления, свободные колебания в среде с сопротивлением, вынужденные колебания в среде без сопротивления, случай резонанса.

1. Обыкновенные дифференциальные уравнения. Основные определения и понятия (порядок уравнения, решение, общее и частное решение, задача Коши, теорема существования и единственности решения).

2. Геометрический смысл дифференциального уравнения первого порядка.

3. Уравнения с разделяющимися переменными.

4. Однородные дифференциальные уравнения первого порядка.

5. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.

6. Метод вариации произвольной постоянной.

7. Уравнение Я. Бернулли.

8. Уравнения в полных дифференциалах. Необходимое и достаточное условие.

9. Интегрирующий множитель.

10. Приближенное решение дифференциального уравнения первого порядка методом Эйлера.

11. Дифференциальные уравнения первого порядка высших степеней.

12. Дифференциальные уравнения второго порядка: основные понятия (решение, общее и частное решения, общий и частный интеграл).

13. Геометрический смысл дифференциального уравнения второго порядка.

14. Уравнения, допускающие понижение порядка (три типа).

15. Дифференциальные уравнения п-го порядка. Основные понятия.

16. Линейные дифференциальные уравнения второго порядка. Основные понятия.

17. Линейные однородные дифференциальные уравнения второго порядка. Свойство их решений.

18. Линейная зависимость функций. Определитель Вронского, его свойства. Фундаментальная система решений.

19. Теорема о структуре общего решения линейного дифференциального уравнения 2-го порядка.

20. Линейные однородные дифференциальные уравнения п-го порядка.

21. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами (три случая при решении характеристического уравнения)

22. Линейные однородные дифференциальные уравнения п-го порядка с постоянными коэффициентами.

23. Линейные неоднородные дифференциальные уравнения 2-го порядка. Теорема о структуре общего решения линейного неоднородного дифференциального уравнения 2-го порядка.

24. Метод вариации произвольных постоянных.

25. Теорема о наложении решений.

26. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и правой частью специального вида.

27. Линейные неоднородные дифференциальные уравнения п-го (п>2) порядка с постоянными коэффициентами и правой частью специального вида.

28. Системы дифференциальных уравнений, основные понятия (нормальная система, теорема Коши и др.).

29. Системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами.

30. Приложение линейных дифференциальных уравнений к изучению колебательных процессов: свободные колебания в среде без сопротивления, свободные колебания в среде с сопротивлением, вынужденные колебания в среде без сопротивления, случай резонанса.

1. Обыкновенные дифференциальные уравнения. Основные определения и понятия (порядок уравнения, решение, общее и частное решение, задача Коши, теорема существования и единственности решения).

2. Геометрический смысл дифференциального уравнения первого порядка.

3. Уравнения с разделяющимися переменными.

4. Однородные дифференциальные уравнения первого порядка.

5. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.

6. Метод вариации произвольной постоянной.

7. Уравнение Я. Бернулли.

8. Уравнения в полных дифференциалах. Необходимое и достаточное условие.

9. Интегрирующий множитель.

10. Приближенное решение дифференциального уравнения первого порядка методом Эйлера.

11. Дифференциальные уравнения первого порядка высших степеней.

12. Дифференциальные уравнения второго порядка: основные понятия (решение, общее и частное решения, общий и частный интеграл).

13. Геометрический смысл дифференциального уравнения второго порядка.

14. Уравнения, допускающие понижение порядка (три типа).

15. Дифференциальные уравнения п-го порядка. Основные понятия.

16. Линейные дифференциальные уравнения второго порядка. Основные понятия.

17. Линейные однородные дифференциальные уравнения второго порядка. Свойство их решений.

18. Линейная зависимость функций. Определитель Вронского, его свойства. Фундаментальная система решений.

19. Теорема о структуре общего решения линейного дифференциального уравнения 2-го порядка.

20. Линейные однородные дифференциальные уравнения п-го порядка.

21. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами (три случая при решении характеристического уравнения)

22. Линейные однородные дифференциальные уравнения п-го порядка с постоянными коэффициентами.

23. Линейные неоднородные дифференциальные уравнения 2-го порядка. Теорема о структуре общего решения линейного неоднородного дифференциального уравнения 2-го порядка.

24. Метод вариации произвольных постоянных.

25. Теорема о наложении решений.

26. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и правой частью специального вида.

27. Линейные неоднородные дифференциальные уравнения п-го (п>2) порядка с постоянными коэффициентами и правой частью специального вида.

28. Системы дифференциальных уравнений, основные понятия (нормальная система, теорема Коши и др.).

29. Системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами.

30. Приложение линейных дифференциальных уравнений к изучению колебательных процессов: свободные колебания в среде без сопротивления, свободные колебания в среде с сопротивлением, вынужденные колебания в среде без сопротивления, случай резонанса.

1. Обыкновенные дифференциальные уравнения. Основные определения и понятия (порядок уравнения, решение, общее и частное решение, задача Коши, теорема существования и единственности решения).

2. Геометрический смысл дифференциального уравнения первого порядка.

3. Уравнения с разделяющимися переменными.

4. Однородные дифференциальные уравнения первого порядка.

5. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.

6. Метод вариации произвольной постоянной.

7. Уравнение Я. Бернулли.

8. Уравнения в полных дифференциалах. Необходимое и достаточное условие.

9. Интегрирующий множитель.

10. Приближенное решение дифференциального уравнения первого порядка методом Эйлера.

11. Дифференциальные уравнения первого порядка высших степеней.

12. Дифференциальные уравнения второго порядка: основные понятия (решение, общее и частное решения, общий и частный интеграл).

13. Геометрический смысл дифференциального уравнения второго порядка.

14. Уравнения, допускающие понижение порядка (три типа).

15. Дифференциальные уравнения п-го порядка. Основные понятия.

16. Линейные дифференциальные уравнения второго порядка. Основные понятия.

17. Линейные однородные дифференциальные уравнения второго порядка. Свойство их решений.

18. Линейная зависимость функций. Определитель Вронского, его свойства. Фундаментальная система решений.

19. Теорема о структуре общего решения линейного дифференциального уравнения 2-го порядка.

20. Линейные однородные дифференциальные уравнения п-го порядка.

21. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами (три случая при решении характеристического уравнения)

22. Линейные однородные дифференциальные уравнения п-го порядка с постоянными коэффициентами.

23. Линейные неоднородные дифференциальные уравнения 2-го порядка. Теорема о структуре общего решения линейного неоднородного дифференциального уравнения 2-го порядка.

24. Метод вариации произвольных постоянных.

25. Теорема о наложении решений.

26. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и правой частью специального вида.

27. Линейные неоднородные дифференциальные уравнения п-го (п>2) порядка с постоянными коэффициентами и правой частью специального вида.

28. Системы дифференциальных уравнений, основные понятия (нормальная система, теорема Коши и др.).

29. Системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами.

30. Приложение линейных дифференциальных уравнений к изучению колебательных процессов: свободные колебания в среде без сопротивления, свободные колебания в среде с сопротивлением, вынужденные колебания в среде без сопротивления, случай резонанса.