30. Приложение лду к изучению колебательных процессов.
30.1 Свободные колебания в среде без сопротивления.
Пусть тело массой m подвешено на упругой нити, которая неподвижно закреплена одним концом. В исходном состоянии равновесия длина нити равна l. Коэффициент упругости r>0.
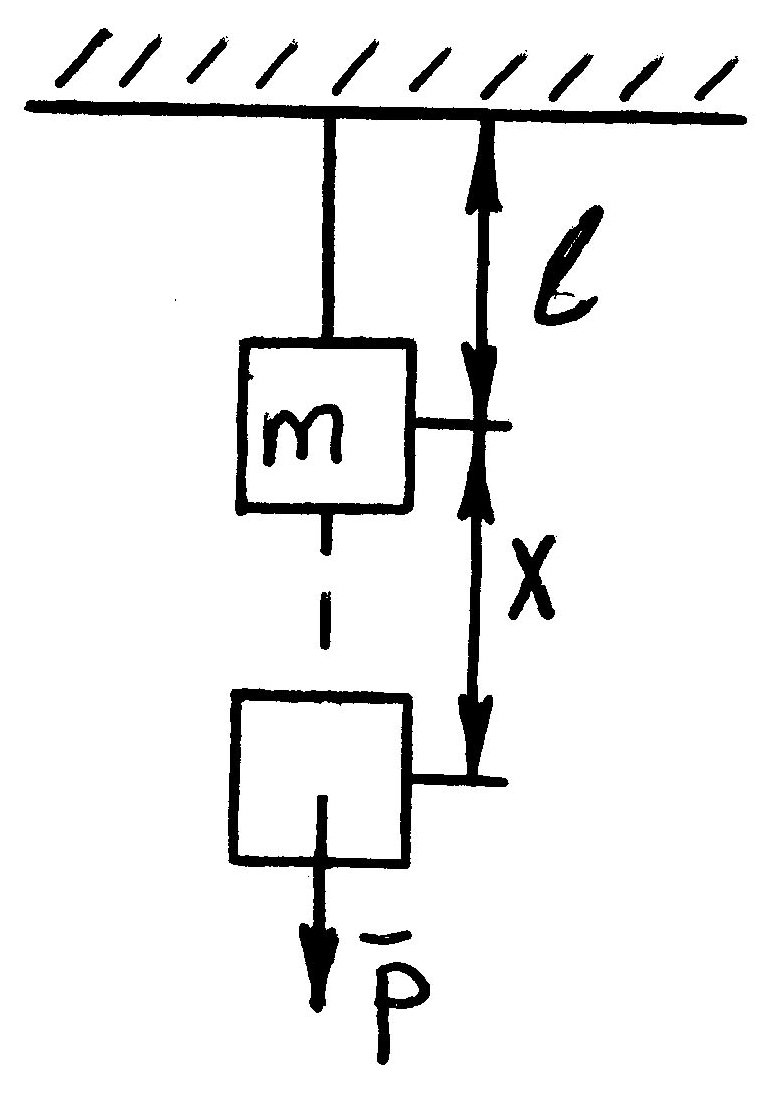
Если вывести тело из состояния равновесия, то оно отклонится вверх или вниз на величину X. Нужно найти зависимость X(t).
Используя физические законы, получим, что ДУ, которому удовлетворяет X(t) имеет вид
(1)
Разделив обе части на m, получим
;
Пусть
,
получим
(2)
Это уравнение является однородным ДУ-2 с постоянными коэффициентами.
Для его решения составим и решим характеристическое уравнение
k²+w²=0
k²=- w²
k1,2=±wi
таким образом общее решение уравнения (2) имеет вид
α=0 , β=ω
x(t)=c1 ∙ sin (wt) + c2 ∙ cos (wt) (3)
чтобы выяснить
физический смысл полученного уравнения
преобразуем его, домножив и разделив
на
(4)
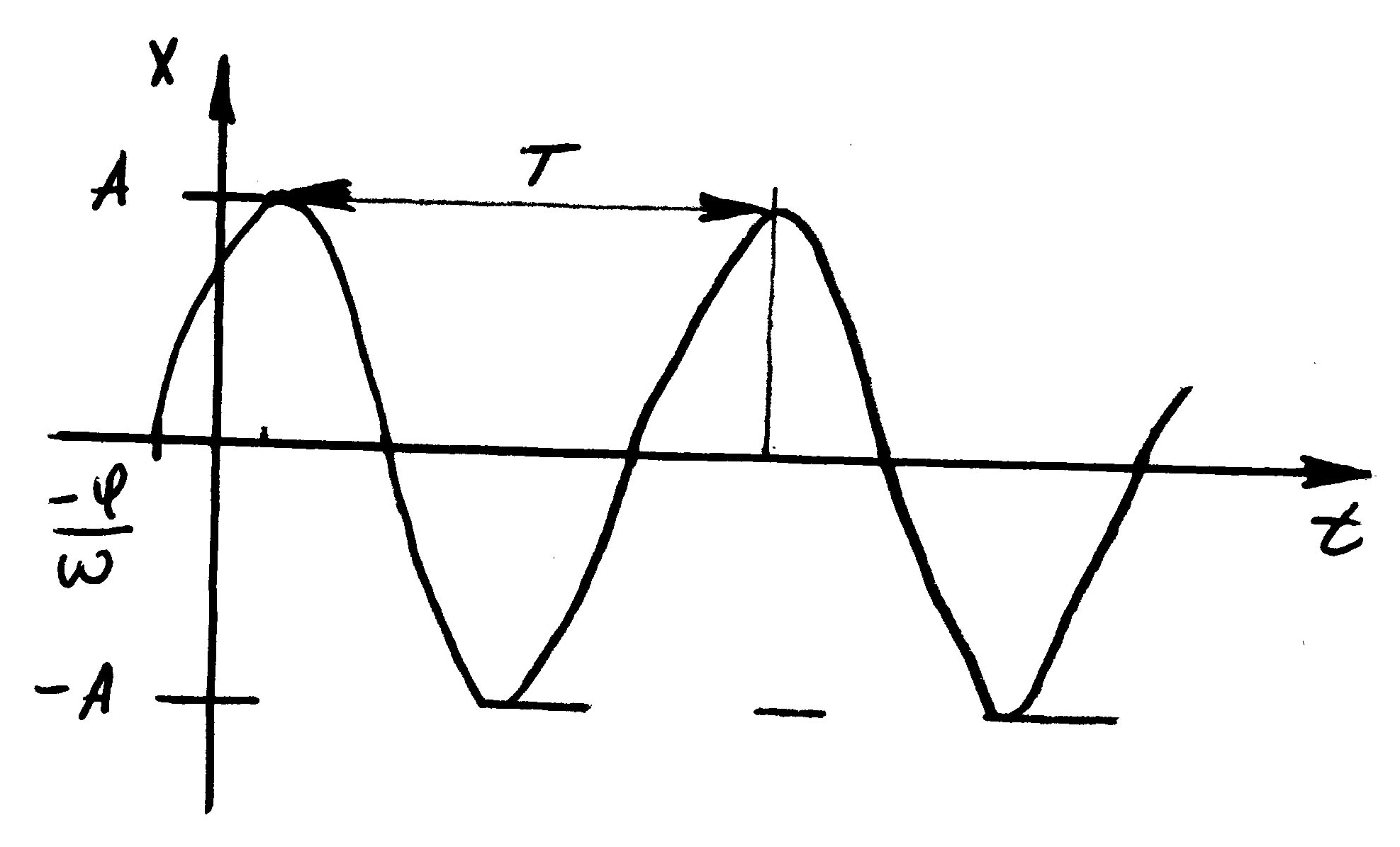
Получим, что x(t) меняется по синусоидальному закону.
Говорят, что тело совершает свободные гармонические независимые колебания около положения равновесия.
Здесь А – амплитуда, w – частота, φ – начальная фаза, T=2П/W – период колебаний.
Из формулы
видно, что частота тем больше, чем больше
r
и меньше m.
Чтобы получить определенное решение нужно задать начальные условия
,
(5)
То из (4) и (5) получим систему уравнений для определения А и φ.
Отсюда находим А и φ.
______________________
30.2 Свободные колебания в среде с сопротивлением
Пусть при движении тело испытывает сопротивление, сила которого пропорциональна скорости движения (коэффициент пропорциональности r1).
То уравнение движения:
Обозначим
(6)
Составим и решим характеристическое уравнение:
(7)
Рассмотрим возможные случаи в зависимости от соотношения δ и ω.
пусть δ < ω то есть сопротивление среды достаточно мало по сравнению с силой упругости пружины. На практике чаще всего встречается именно этот случай, когда колебания происходят в воздушной среде, то
следовательно,
аналогично случаю 1 домножим и разделим
на
и
введем переобозначания
(8)
В этом случае движение тоже является колебательным с частотой w1<w и начальной фазой φ, но здесь амплитуда колебаний уменьшается с течением времени по экспоненциальному закону, говорят, что тело совершает затухающие колебания.
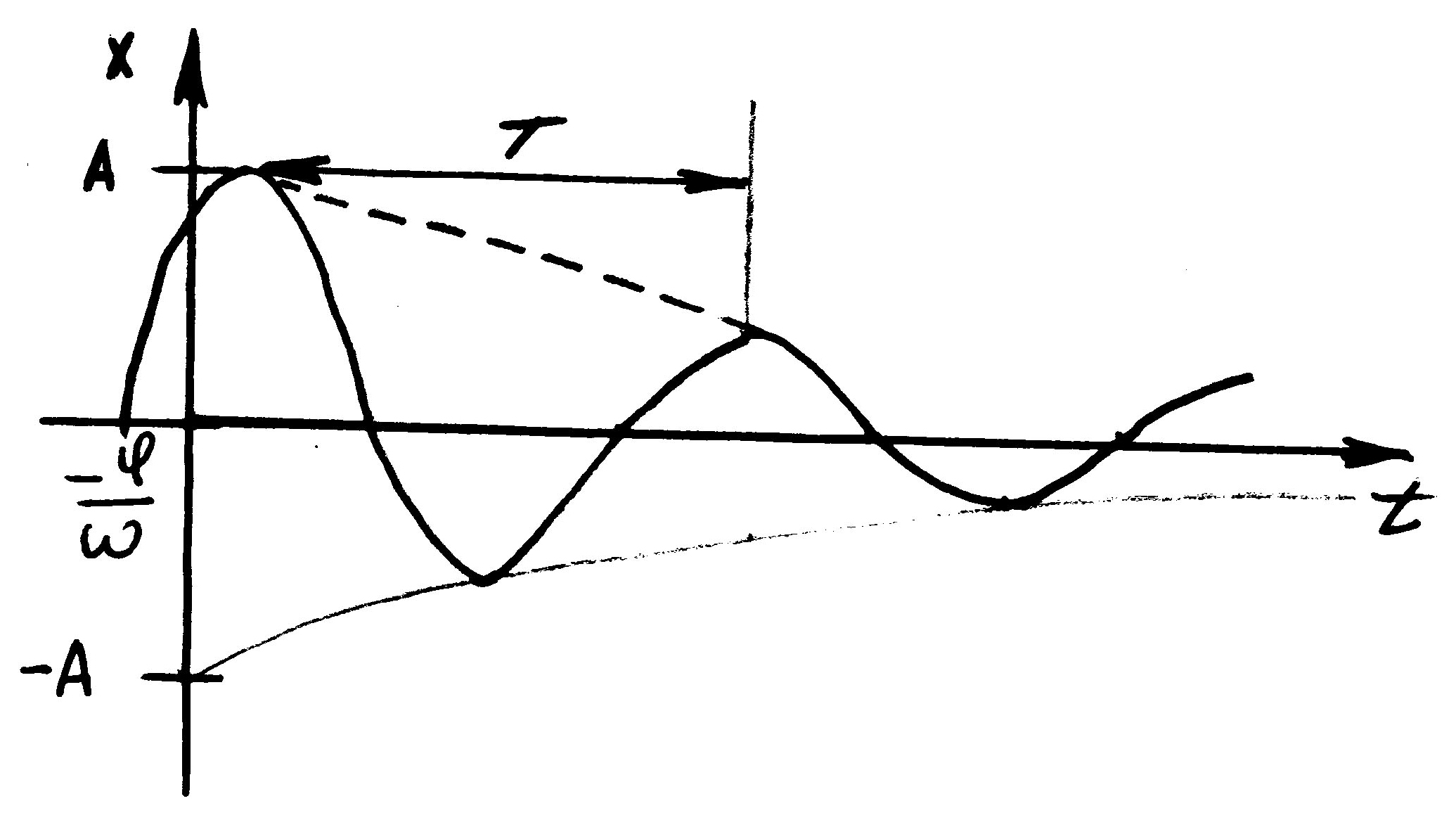
пусть δ > ω то есть сопротивление среды велико, среда вязкая и в этом случае корни характеристического уравнения действительны и отрицательные:
То общее решение имеет вид
(9)
Таким образом колебаний нет. После отклонения тело медленно возвращается в положение равновесия.
δ = ω, то есть сопротивление среды тоже достаточно велико. В этом случае характеристическое уравнение 2 равных действительных корня, следовательно общее решение:
(10)
Как видим, и в этом случае колебаний нет. Картина примерно та же, что и в пункте 2.
______________________