1. Обыкновенные д.У. Основные определения.

О₁. Обыкновенные д.у. наз-ся ур-я связывающие независимую прм Х, искомую ф-ции y=y(x) и произв. Искомой ф-ции до некоторых порядка включительно.

О₂. Порядка д.у. наз-ся порядок наивысшей производной входящей в это ур-е.

Обык-ные д.у. I порядка имеет вид F(x;y;y’)=0(1.1)

Обык-ные д.у. II порядка имеет вид F(x;y;y’;y”)=0(1.2)

О₃ Решение д.у. наз-ся всякая ф-ция, кот-ая при подстановке в ур-е обращается его в тождество.

Д.у. I порядка.

Д.у. I порядка имеет вид F(x;y;y’)=0(2.1), где Х - незав-я прм; y – иск-я ф-ция; y’ – её произ-ная

Если ур-е 2.1. разрешить относительно производной, то получим ур-е y’=f(x;y)(2.2), кот-ое наз-ся уравнением I порядка разрешенным отн-но производной.

Д.у. I порядка разрешенное отн-но произ-ной можно записать в диф-ной форме или в диф-лах.

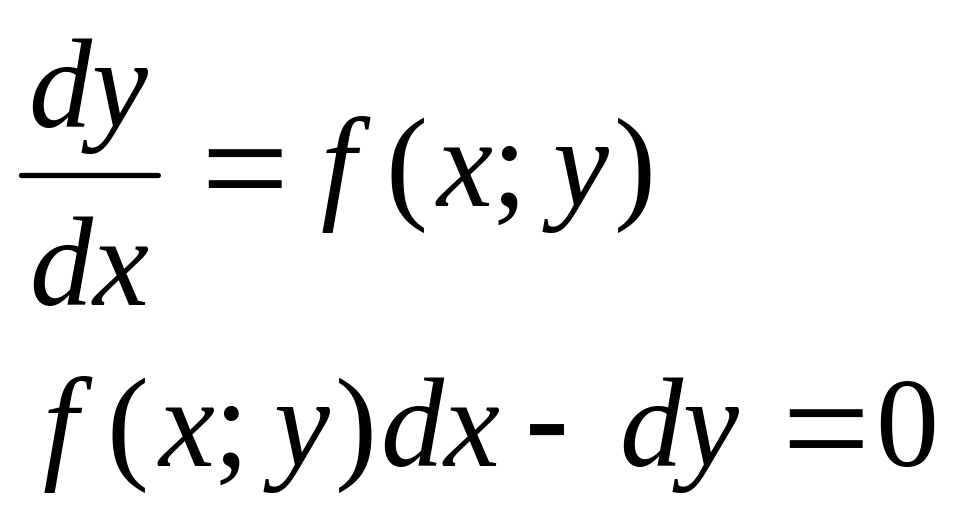этот вид является частным случаем более общего ур-я.

F(x;y)dx+Q(x;y)dy=0(*), где F(x;y) и Q(x;y) – известные ф-ции.

Замечание, ур-е вида * наз-ют также симметричной формы.

Д.у. I порядка имеют бесконечное множество решений, кот-ые определяются формулой, содержащую одну производную постоянную.

О1.Общим решением д.у. 2.1. или 2.2. наз-ся ф-ция у=у(х;С), кот-рая при любом постоянном значении С удовлетворяет ур-е 2.1 или 2.2.

О2. Частные решениям д.у. I порядка наз-ся такое решение, кот-ое получено из общего при некотором вполне определенном значение постоянной С.

Y’= - y/x

Y=c/x – является общим решение ур-е, т.к. это ф-ции удовлетворяет ур-е при любом постоянном значении Х.

Ф-ция у=2/х при с=2 явл. частным решением.

График любого частного решения наз-ся интегральной кривой. Общему решению у=у(х;c) соответственно семейство интегральных кривых.

На практике искомое частное решение данного уравнения получают из общего не заданного С, а исходящего из тех условий кот-ых должно удовлетворять искомое частного решение.

Пусть дано ур-е у’=f(x;y), для кот-ого общие решение ф-ции y=y(x;c) и требуется найти частное решение, кот-е удовлетворяет заданным начальным условиям y₀=y(x₀)(2.3.)

Условие 2.3 означают, что ф-ция Y равна Y₀ при значении X=X₀

Найти частное решение удовлетворяющего заданным начальным условиям 2.3. геометрически означает, что из семейства интегр-х кривых, кот-е соотв-ет общему решению, надо y=y(x;c) выделить ту единственную кривую, кот-я проходит через т.P₀(x_0; y₀) в плоскости D_XY.

Задача отыскания частного решения ур-я 2.2. удовлетворяемая заданными условиям, наз-ся задачей Коши.

Для д.у. I порядка задача коши сводится к отысканию частного решения, кот-ое при х=х₀ принимает заданное значение у=у₀.

Условие, при котором д.у.(2.2) имеет частное решение, удовлетворяющие данным начальных условий(2.3) могут быть сформулированы в виде след. теоремы.

Теорема о сущ-нии единственности решения (T. Коши)

Если ф-ия f(х,у) непрер-а в области, содержащей точку Р0(х0,у0), то ДУ y’=f (x,y) имеет частное решение у=у(х) такое, к-ое удовлетворяет ур-ию у(х0)=у0. Если кроме того непрерывна и частная произ-ая df/dy в точке Р0, то решение единственное..

Точки, в которых теорема Коши нарушается называется особыми точками.

Соотношения вида F(x;y;с)=0 не явно определено.Общим решением вида 2.1 или 2.2 называются общим интегральным д.у.

Соотношения вида F(x;y;с₀)=0, где с₀ – определяется значением производной постоянной называется частным интегралом д.у.

______________________