1. Арифметическое пространство Rn

 

         Величина, которая полностью характеризуется своим числовым значением в выбранной системе единиц, называется скалярной или скаляром (масса, объем, температура). Скаляр определяется числом, положительным, отрицательным или равным нулю. Если величина характеризуется еще и направлением, то она называется векторной или вектором (сила, скорость и так далее). Таким образом, вектор определяется числом и направлением.

         Многие вопросы как теоретического, так и прикладного характера приводят к рассмотрению упорядоченных совокупностей чисел (величин). Например, план работы предприятия, выраженный в определенных числовых показателях, рост цен за ряд лет и так далее. Если отвлечься от конкретного смысла объектов, мы приходим к следующему понятию.

 

Определение 1.1. Множество всех упорядоченных совокупностей по n чисел (х₁,х₂,...,х_n) называется арифметическим n-мерным пространством (Rⁿ)

(n - размерность пространства).

 

         Будем теперь предполагать, что на плоскости или в пространстве всегда фиксирована некоторая прямоугольная система декартовых координат. Тогда каждая точка будет определена своими координатами А(х₁,х₂,...,х_n), В(у₁,у₂,...,у_n).

         Арифметическое пространство R¹ (или R) образует множество действительных чисел. R² представляет собой плоскость, при этом имеем

.

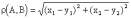R³ - это трехмерное пространство; при этом имеем

.

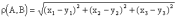В случае Rⁿ  мы имеем дело с n-мерным пространством и тогда

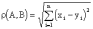.                                                   (1.1)

 

Определение 1.2. Совокупность точек n-мерного пространства, для которых определено расстояние по формуле (1.1), называется n-мерным Евклидовым пространством.

 

         Свойства расстояния между двумя точками:

                   1. (А,В)  0,  причем если (А,В) = 0, следовательно, А = В.

                   2. (А,В) = (В,А) для всех точек А, В  Rⁿ,

                   3. (А,C)  (A,В) + (B,C) для всех точек А, В, C  Rⁿ

Эта тема есть в задачнике – Данко, Попов.. стр. 103

2. Понятие вектора и линейные операции над векторами.

Под вектором в элементарной математике понимают направленный отрезок. Этот отрезок изображается стрелкой и обозначается или одной буквой со стрелкой (  )

Операции над векторами:

Сложение векторов

Сумму двух неколлинеарных векторов   и 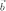  можно найти по правилу параллелограмма,и треугольника.

Вычитание векторов

Разностью векторов   и   называется сумма вектора   с вектором 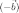 , противоположным вектору  :

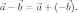
Умножение вектора на число

Произведением ненулевого вектора   на действительное число 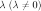  называется вектор 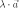 , удовлетворяющий условиям:

1) длина вектора   равна  , т.е.  ;

2) векторы   и   коллинеарные  ;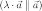

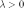3) векторы   и   одинаково направлены, если  , и противоположно направлены, если  .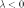

3. Скалярное произведение и его свойства.

Скаля́рное произведе́ние (в зарубежной литературе - scalar product, dot product, inner product ) — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины вектора x на проекциювектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.

• теорема косинусов легко выводится с использованием скалярного произведения:

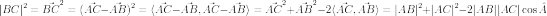
• Угол между векторами:

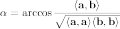
• Оценка угла между векторами:

в формуле 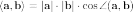  знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой.

• Проекция вектора   на направление, определяемое единичным вектором  :

,

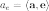• условие ортогональности^[2] (перпендикулярности) векторов   и  :

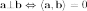
• Площадь параллелограмма, натянутого на два вектора   и  , равна

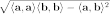
4. Угол между векторами — угол между направлениями этих векторов (наименьший угол).

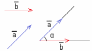
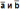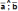По определению, угол между двумя векторами находится в промежутке [0°; 180°]. Угол между векторами   обозначается так:  . Если векторы перпендикулярны, то угол между ними равен 90º. Если векторы сонаправлены, в частности один из них или оба нулевые, то угол между ними равен 0^о. Если противоположно направленные векторы, то угол между ними равен 180º. Угол между двумя ненулевыми векторами находится с помощью вычисления скалярного произведения. По определению скалярное произведение равно произведению длин векторов на косинус угла между ними (скалярное произведение для двух векторов с координатами (x₁; y₁) и (x₂; y₂) вычисляется по формуле: x₁x₂ + y₁y₂).