Плоскость

Рассмотрение поверхностей начнем с самой простой из них – плоскости.

Плоскость – это поверхность, обладающая тем свойством, что всякая прямая соединяющая две ее точки, лежит в ней целиком.

Рассматривая поверхности мы будем иметь ввиду только кинематический способ образования поверхности. Отсюда плоскость – это поверхность, образованная движением прямой линии «а» (образующей), скользящей по двум пересекающимся прямым (направляющим).

Плоскость можно задать (рис. 1.10):

а) тремя точками, не лежащими на одной прямой;

б) прямой а и точкой М, не лежащей на этой прямой;

	в) двумя пересекающимися прямыми а и в или двумя параллельными прямыми с и d; г) плоской фигурой , например, треугольником ABC.
Рис. 1.10

Условимся плоскости обозначать греческими буквами.

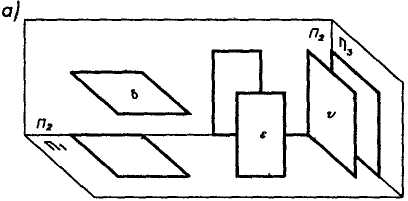
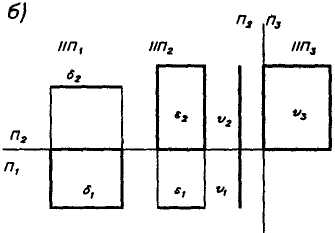
	Плоскость общего положения наклонена к плоскостям проекций (рис. 1.11). Ни на одну плоскость про­екций она не проецируется в прямую линию. Плоскости частного положения параллельны или перпендикулярны плоскостям проекций. На рис. 1.12а показаны плоскости, параллельные одной из плоскостей проекций: S - горизонтальная, е - фронтальная, v - профильная (заданы прямоугольниками). Каждая плоскость проецируется на одну из плоскостей проекций в нату­ральную величину, другие же их проекции - прямые линии, перпендикулярные линиям связи (рис. 1.126).
Рис. 1.10
Рис. 1.12

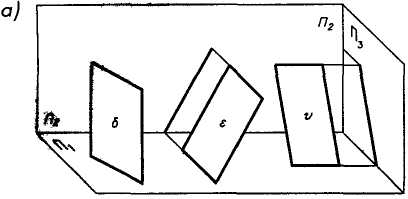
На рис. 1.13а показаны плоскости, перпендикулярные только одной плоскости проекций и не параллельные двум другим плоскостям проекций (проецирующие): 5— горизонтально-проеци­рующая; е - фронтально-проецирующая; v - профильно-проецирующая. На рис. 1.13б даны их проекции.

Рис. 1.13

Плоскость 5 проецируется на плоскость Л₁ в прямую линию. Все, что на ней расположено, - точки, прямые и др. элементы (рис. 1.14) - проецируются на эту линию, поэтому плоскость называется проецирующей. Углы, образованные этой плоскостью с другими плоскостями проекций, проецируются в натураль­ную величину (рис. 1.136). Фронтальная проекция 8₂ не дает натуральной ве­личины фигуры. Аналогичными свойствами обладают другие проецирующие плоскости.

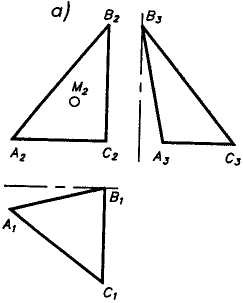
Проекции точки плоскости общего положения (рис. 1.15) строят с помощью вспомогательных прямых. Пусть даны три проекции треугольника и проекция М₂ лежащей на нем точки (рис. 1.15а). Проведем через точку М прямую, параллель­ную одной из сторон треугольника (прямая может быть проведена произвольно, например через точку М и любую вешпину треу­гольника): сначала фронтальную и профильную (рис. 1.156) проекции, затем через i_i горизон­тальную, параллельно одноименной проекции (AfiJ стороны треугольника. Построим проек­цию точки М_г Зададимся фронтальной плоско­стью отсчета координат £, проведем ее через вер­шину В треугольника; обозначим ее проекции Ј_f и 4₃ (рис. 1.156). Измерим координату у_м точки М- расстояние от линий £_г до проекции М₁ точ­ки. Проведем на расстоянии упрямую, парал­лельную £,₃, - геометрическое место возможных положений проекции М₃, которую находим на проекции вспомогательной прямой, проведен­ной ранее (рис. 1.15в).

	Рис. 1.15

Поверхность вращения получается в результате вращения вокруг оси некоторой образующей линии, кривой или прямой. В конструкциях часто встречаются поверхности: цилиндр, конус, сфера, тор.

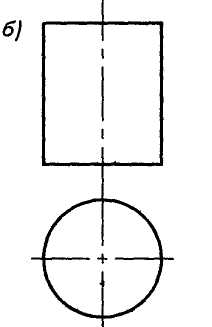
Цилиндр получается при движении образующей тп параллельно самой себе по кривой направляющей я (рис. 1.17а). При направляющей окружности получают­ся круговые цилиндры - прямой (цилиндр вращения, рис. 1.176) и наклонный (рис. i0p).

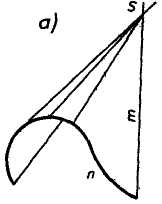
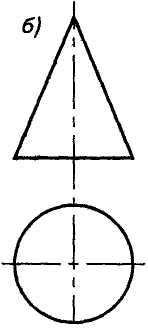
Конус получается в результате движения прямой образующей тп, проходящей через неподвижную точку 5 по кривой направляющей п (рис. 1.18а). При направляющей окружности получаются круговые конусы - прямой (конус вращения, рис. 1.186) и наклонный (рис. 1.18в).

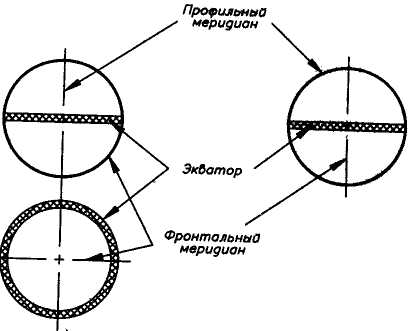
Сфера (рис. 1.19) получается в результате вращения окружности вокруг диаметра.
Тор получается в результате вращения окружности тп вокруг оси - хорды («бочка») или вокруг оси, лежащей в плоскости окружности и не пересекающей ее контур (тор-кольцо, рис. 1.20). Центровой окружностью называют траекторию; вращения центра образующей окружности.

ТОЧКА НА ПОВЕРХНОСТИ ВРАЩЕНИЯ

Находятся с помощью вспомогательных линий

Ххххххххххххххххххххххххххххххххххх\